分布式电源并网逆变器典型控制方法综述
2012-07-02王成山李琰彭克
王成山,李琰,彭克
(天津大学智能电网教育部重点实验室,天津300072)
目前,分布式发电相关技术在世界范围内获得了广泛关注[1,2]。由于分布式电源与接入大电网的电源特性明显不同,后者为同步发电机,而前者中一大类电源输出为直流电或是非工频交流电(如光伏电池、燃料电池、风机等),必须采用并网逆变器上网,因此并网逆变器的研究已成为分布式发电领域的一个研究热点[3~7]。分布式电源既可组成微网运行,也可直接接入常规配电系统运行。当组成微网运行时,对分布式电源的控制方法和控制目标有一些特殊要求,如:微网独立运行时可能需要一些分布式电源改变控制模式;微网的运行状态多变,要求状态转换时尽可能实现无缝切换,等等。
为了对并网逆变器的相关控制有一个比较系统化的了解,本文主要针对微网中分布式电源的并网控制方法进行了总结分析,以供相关研究者参考。由于在分布式发电系统中,电压型逆变器应用较为广泛,同时考虑到三相较单相逆变器更具一般性,因此下面主要以三相电压型逆变器为例介绍其控制系统。
1 三相并网逆变器典型控制结构
三相并网逆变器的控制方式多种多样,目前应用较为广泛的主要有双环控制与多环控制[8,9]。由于多环控制从其控制环节的拓扑结构及实现的功能方面看也可归为双环控制,下面主要从双环控制的角度讨论逆变器的典型控制模式。
在双环控制系统中,外环控制器主要用于体现不同的控制目的,同时产生内环参考信号,一般动态响应较慢。内环控制器主要进行精细的调节,用于提高逆变器输出的电能质量,一般动态响应较快[9]。当并网要求并不是非常高时,也可以采用较简单的控制方式,单独使用外环对逆变器进行控制,但此时并网的电能质量和控制速度并不是非常理想,因此目前应用较多的是双环控制方式。
根据坐标系选取的不同,内环控制器可以分为dq旋转坐标系下的控制、αβ静止坐标系下的控制、abc自然坐标系下的控制[9]。
图1所示为三相电压型逆变器控制系统典型结构示意图[8]。
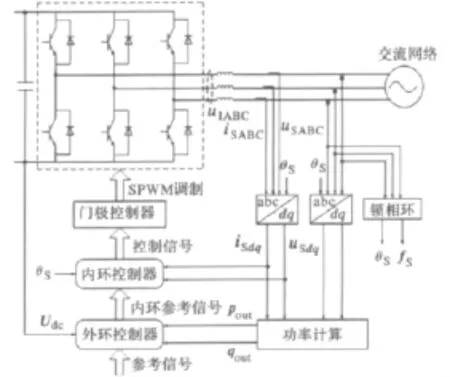
图1 三相逆变器控制系统典型结构Fig.1 Typical structure of control system for three-phase inverter
图1中,Udc为直流侧电压,uIABC、iSABC与uSABC分别为三相逆变器的输出电压、输出电流及交流网络侧电压,iSdq与uSdq分别为iSABC与uSABC经过Park变换后的d轴和q轴分量,fS与θS分别为所接交流母线处电压的频率和A相电压的相角,pout与qout分别为计算所得的逆变器输出的瞬时功率。
2 三相并网逆变器外环控制器
分布式电源的类型及并网控制的目的不同,其并网逆变器也需要采取不同的控制策略,这种控制策略的不同主要体现在逆变器的外环控制。常见的分布式电源并网逆变器的外环控制方法可以分为:
(1)恒功率控制(又称PQ控制);
(2)恒压恒频控制(又称V/f控制);
(3)下垂控制(又称Droop控制)。
2.1 恒功率控制
采用恒功率控制的主要目的是使分布式电源输出的有功功率和无功功率等于其参考功率,即当并网逆变器所连接交流网络系统的频率和电压在允许范围内变化时,分布式电源输出的有功功率和无功功率保持不变。恒功率控制的实质是将有功功率和无功功率解耦后分别进行控制,其控制原理如图2所示。
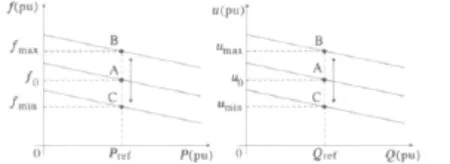
图2 恒功率控制原理Fig.2 Theory of constant power control
分布式电源系统的初始运行点为A,输出的有功功率和无功功率分别为给定的参考值Pref与Qref时,系统频率为f0,分布式电源所接交流母线处的电压为u0。有功功率控制器调整频率下垂特性曲线,在频率允许的变化范围内(fmin≤f≤fmax),使分布式电源输出的有功功率维持在给定的参考值;无功功率控制器调整电压下垂特性曲线,在电压允许的变化范围内(umin≤u≤umax),输出的无功功率维持在给定的参考值。
因此,采用该种控制方式的分布式电源并不能维持系统的频率和电压,如果是一个独立运行的微网系统,则系统中必须有维持频率和电压的分布式电源,如果是与常规电网并网运行,则由常规电网维持电压和频率。根据上述控制原理,图3给出了一种典型的恒功率外环控制器结构。
图3中,对三相瞬时值电流iSABC与三相瞬时值电压uSABC进行Park变换后,得到dq轴分量iSdq、uSdq,进而获得瞬时功率,所得的瞬时功率pout与qout经低通滤波器后得到平均功率Pfilt与Qfilt,该量与所给定的“参考信号”Pref与Qref进行比较,并对误差进行PI控制,从而得到内环控制器的参考信号Idref与Iqref。

图3 恒功率外环控制器典型结构Fig.3 Typical structure of outer-loop controller in constant power control system
在上述“恒功率控制”模式中,由于有功功率和无功功率控制是解耦的,因此若将某一个控制通道或是上述两个控制通道的输入信号和参考信号进行一定的改变,也可得到其他的恒定参考值控制方式。
如下述所介绍的三种恒功率控制变形方式:恒直流电压恒无功功率控制[8~10]、逆变器输出电压控制[11,12]、简化的恒功率控制[13]。
图4中,用直流电压Udc及参考值Udcref分别代替图3中的有功功率pout及参考信号Pref,从而可以将有功功率控制通道转变为直流电压控制通道。其输出信号仍然作为内环控制器的参考信号。
图5中,对逆变器输出的电压进行Park变换可得到uId、uIq,将其替代图3中有功功率pout及无功功率qout,即可实现对逆变器输出电压的控制。
输出信号作为内环控制器的参考信号。其中电压参考信号uIdref与uIqref既可以直接给定,也可以通过计算得到。
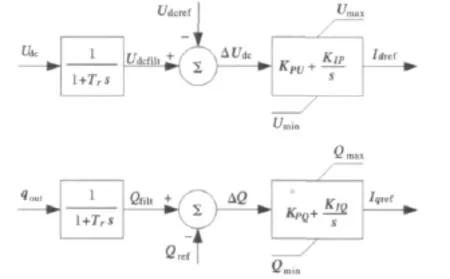
图4 恒直流电压恒无功功率控制器典型结构Fig.4 Typical structure of outer-loop controller for constant dc voltage-constant reactive power control

图5 逆变器输出电压控制典型结构Fig.5 Typical structure of outer-loop controller for output voltage control
由于分布式电源系统注入交流网络的功率可表示为

式中:Z代表逆变器与交流网络之间的电抗;φZ代表线路阻抗角;US代表交流网络侧电压幅值;UI代表逆变器输出电压的幅值;φ代表逆变器输出电压的相角。假定给定逆变器输出功率参考值,则逆变器输出电压的幅值及相角参考值如下式所示。
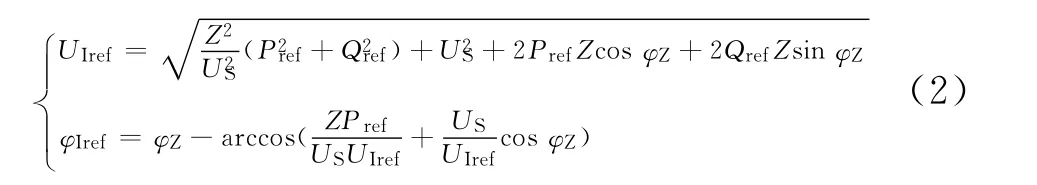
式中,Pref与Qref代表参考功率,其他符号与式(1)含义一致。利用电压幅值及相角的参考值,可以得到三相电压的参考值,进而可以得到dq坐标系下的参考值uIdref与uIqref,实现外环控制过程。由于在dq坐标系下,分布式电源系统注入交流网络的功率为
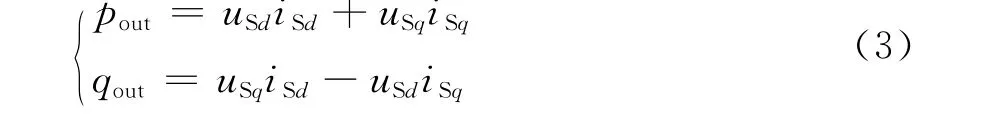
如果Park变换中选取d轴与电压矢量同方向,可使得q轴电压分量为零,如图6所示。
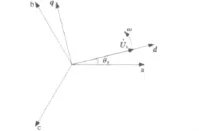
图6 dq轴与电压矢量关系图Fig.6 Relationship between dq axis and voltage vector
此时,功率输出表达式可得到简化,有功功率仅与d轴有功电流有关,而无功功率仅与q轴无功电流有关,从而可以通过功率参考值与交流网络侧电压值计算得到电流参考值,如式(4)所示,该种控制是一种简化的恒功率控制模式。

2.2 恒压恒频控制
采用恒压恒频控制的目的是不论分布式电源输出的功率如何变化,逆变器所接交流母线的电压幅值和系统输出的频率维持不变,其控制原理如图7所示。

图7 恒压恒频控制原理Fig.7 Theory of constant voltage-constant frequency control
图7中,分布式电源系统的初始运行点为A,系统输出频率为fref,分布式电源所接交流母线处的电压为Uref,分布式电源输出的有功功率和无功功率分别为P0与Q0。频率控制器通过调节分布式电源输出的有功功率,使频率维持在给定的参考值;电压调节器调节分布式电源输出的无功功率,使电压维持在给定的参考值。该种控制方式主要应用于微网孤岛运行模式,处于该种控制方式下的分布式电源为微网系统提供电压和频率支撑,相当于常规电力系统中的平衡节点。根据上述控制原理,图8给出了一种典型的恒压恒频外环控制器结构。

图8 恒压恒频外环控制器典型结构Fig.8 Typical structure of outer-loop controller for constant voltage-constant frequency control

2.3 下垂控制
下垂控制[14]是模拟发电机组“功频静特性”的一种控制方法。由于逆变器通过一段电抗连接至交流网络时,注入交流网络的功率如下式所示,相当于式(1)中Z=X且φZ=90°,式中各个符号的含义与式(1)中的一致。
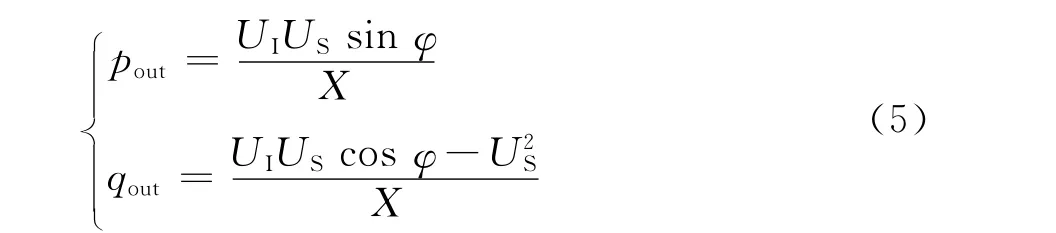
因此当上式中逆变器输出电压的相角φ较小时,sinφ≈φ且cosφ≈1,注入交流网络的有功功率和电压相角呈线性关系,而无功功率和电压幅值成线性关系。下垂控制正是利用该原理进行控制,其控制原理如图9所示。

图9 下垂控制原理Fig.9 Theory of droop control
图9中,当系统有功负荷突然增大时,有功功率不足,导致频率下降;系统无功负荷突然增大时,无功功率不足,导致电压幅值下降。反之亦然。存在两种基本的下垂控制方法:(a)通过调节电压频率和幅值控制输出的功率;(b)通过调节输出的功率控制电压频率和幅值。
(a)f-P和V-Q下垂控制方法:基本思想是通过系统频率和分布式电源系统所接交流母线处电压幅值的测量值,利用相关的下垂特性确定分布式电源有功功率和无功功率的输出参考值,典型控制器框图如图10所示。
图10中,控制器框图包含两个环节:外部“下垂控制”环节和内部“功率控制”环节。外部下垂控制环节输出分布式电源有功功率和无功功率的输出参考值,可以实现各个分布式电源(采取下垂控制)间的负荷功率分摊。内部功率控制环节与图3中“功率调节”一致,为电流环提供电流参考值。

图10 基于f-P和V-Q下垂控制方法的外环控制器Fig.10 Outer-loop controller based on f-P and V-Qdroop control method
(b)P-f和Q-V 下垂控制方法:基本思想是通过分布式电源输出的有功功率和无功功率的测量值,利用相关下垂特性确定频率和电压幅值的参考值,典型控制器框图如图11所示。
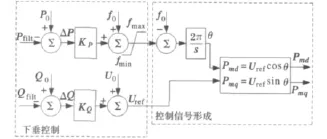
图11 基于P-f和Q-V下垂控制方法的外环控制器Fig.11 Outer-loop controller based on P-f and Q-Vdroop control method
图11中,P-f和Q-V“下垂控制”输出频率和电压幅值的参考值,该参考值经过“控制信号形成”环节后可直接用于并网逆变器的控制。即通过分布式电源输出的有功功率调节逆变器输出的电压相角,采用无功功率调节逆变器输出的电压幅值,这是一种仅存在外环的单环控制方式。由于上述单环控制方式中,逆变器输出的电压受负荷不对称或负荷非线性的影响较大,为了避免逆变器输出电压的波动,可在下垂控制方法中增加电压控制[15,16]。
除了上述控制方法外,下垂控制还存在其他的控制方式,例如文献[17,18]提出了一种虚拟阻抗法,采用Q-L特性代替Q-V特性实现电压控制;文献[19]在考虑低压配电线路呈阻性特点的基础上,提出了P-V和Q-f控制方法,采用有功功率控制电压幅值,采用无功功率控制输出频率。
3 三相并网逆变器内环控制器
内环控制器主要对注入网络的电流进行调节,从而提高电能质量,改善系统的运行性能。从采取不同坐标系的角度,内环控制器又可分为[8,9,20~24]:(1)dq 旋转坐标系下 的控制;(2)αβ 静止坐标系下的控制;(3)abc自然坐标系下的控制。其中“dq旋转坐标系下的控制”使用最为普遍。
3.1 dq旋转坐标系下的控制
该种控制是基于Park变换思想,将三相瞬时值信号变换到dq旋转坐标系下[8,9,20~24],从而将三相控制问题转化为两相控制问题。由于图1所示并网逆变器的电路方程为

式中L表示逆变器出口与交流网络之间的单相电感参数,iSd、iSq分别为注入网络电流经过Park变换后的d轴和q轴分量。因此根据式(6),可得dq旋转坐标系下内环控制器的典型结构如图12所示[8,9]。
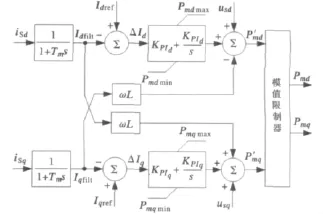
图12 dq坐标系下内环控制器典型结构Fig.12 Typical structure of inner-loop controller in dq frame
图12中,三相瞬时值电流iSABC经Park变换后变换为dq轴分量iSdq,然后经过低通滤波器分别得到Idfilt与Iqfilt,与外环控制器输出的“参考信号”Idref与Iqref进行比较,并对误差进行PI控制,同时限制逆变器输出的最大电流,并通过电压前馈补偿和交叉耦合补偿,输出电压控制信号P′md与P′mq。该控制信号经过模值限制器的限制作用,输出真正的调制信号Pmd与Pmq。在上述控制方式中,电压前馈补偿与交叉耦合补偿的主要目的是将并网方程中的dq分量解耦,分别进行控制。但实际补偿时难以实现完全补偿,因此可采取图13所示的解耦方式的电流闭环控制。

图13 dq坐标系下解耦方式内环控制器典型结构Fig.13 Typical structure of decoupling inner-loop controller in dq frame
图13中所示的电流闭环控制能够抑制交叉耦合项的干扰。由于无补偿环节,电压输出存在误差,从而导致电流iSd、iSq不等于给定值,PI调节器的输入误差信号ΔId、ΔIq导致调制信号Pmd与Pmq产生变化,从而校正由于无补偿环节造成的误差,抑制交叉耦合项的干扰,因此这种电流闭环控制是一种自适应的补偿措施。
图12与图13所示的控制器结构中均涉及“模值限制器”,其主要作用是防止输出调制信号Pmd与Pmq饱和,使得逆变器处于线性调制状态。常用的模值限制器模型分别如图14与图15所示。

图14 模值限制器模型1Fig.14 Model 1of modulus limiter

图15 模值限制器模型2Fig.15 Model 2of modulus limiter
“模值限制器”输出的调制信号Pmd与Pmq经过反Park变换可以得到三相调制信号,从而控制输出的三相电压。另一方面,根据调制信号Pmd与Pmq,可得逆变器输出基波线电压有效值的dq轴分量分别为:

3.2 αβ静止坐标系下的控制
该种控制的基本思想是将三相瞬时值信号变换到αβ 静止坐标系下[8,9,20~25],从而将三相交流控制问题转化为两相交流控制问题。由于在该种变换方式下,控制参数是正弦波动的,而PI调节器的“无静差控制”只是针对直流量,对交流量的调节存在稳态误差,因此在该种控制方式中,一般使用PR(proportional resonant)控制器。αβ静止坐标系下内环控制器的典型结构如图16所示。
PR控制器如图中虚线部分所示,ω为控制器谐振频率,KPPR与KIPR分别为PR控制器的比例增益和积分增益。PR控制器在谐振频率ω附近较窄的带宽内具有较高的增益,从而限制了控制信号和参考信号之间的稳态误差。但较窄的工作带宽限制了PR控制器的调节功能,因此需要采用谐波补偿器对低次谐波进行补偿,图中“HC”代表谐波补偿器。谐波补偿器既可以通过多个PI调节器级联实现,也可以通过多个PR调节器并联实现,当采用多个PR调节器并联时,谐波补偿器的传递函数表达式为
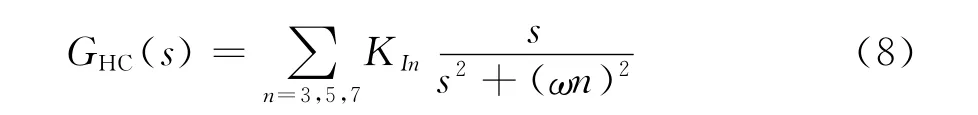
式中,n代表谐波次数。由于PR控制器与谐波补偿器的控制作用均与谐振频率有关,因此为了得到良好的控制效果,其谐振频率必须与网络侧的额定频率一致。该种控制器的优点是可以对低次谐波进行控制,但正是谐波补偿器的存在增加了控制器的复杂性。
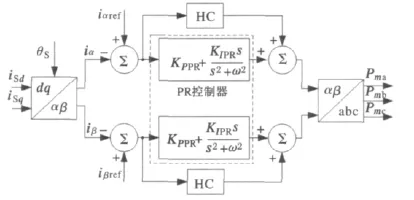
图16 αβ坐标系下内环控制器典型结构Fig.16 Typical structure of inner-loop controller inαβframe
3.3 abc自然坐标系下的控制
该种控制方法的特点是可以获得三相独立的控制器,然而须对三相系统不同的连接方式(星形连接、角形连接、是否采用中线等)进行不同的考虑。abc自然坐标系下内环控制器[8,9,22~24]的典型结构如图17所示。
图17中,“电流控制器”可以采取多种控制器实现[9],例如PI调节器、PR调节器、滞环控制器和死区控制器等。其中PI调节器和PR调节器为线性控制,滞环控制器和死区控制器为非线性控制。当采用PI调节器时,电流控制器的传递函数表达式为[9]

图17 abc坐标系下内环控制器典型结构Fig.17 Typical structure of inner-loop controller in abc frame
式中的非对角线元素代表了相间耦合关系,该种强耦合关系使得电流控制器较为复杂。当采用PR调节器时,电流控制器的表达式如下式所示,可以看出其复杂性明显降低[9]。

从上述三种内环控制方式的介绍可以看出,dq旋转坐标系控制是基于Park变换并采用PI调节器进行控制的,因此该种控制方式更加适用于三相平衡系统;由于αβ静止坐标系控制中采用PR调节器,可以对交流量进行调节,因此该种控制方式可应用于三相非平衡系统,而且由于增加了谐波补偿器,可以对谐波分量进行控制,因此可以实现较为理想的控制效果;abc自然坐标系控制中三相控制系统是相对独立的,因此可应用于三相非平衡系统,但其控制器的结构相对复杂。
4 结语
本文系统地介绍了分布式电源并网逆变器典型的双环控制方法,详细分析了不同的外环控制系统及功能,内环控制系统及不同的应用场景和优缺点。在提倡可持续发展的今天,分布式发电技术是电力工业实施能源变革的重要组成因素。在分布式发电系统中,研究分布式电源并网的不同拓扑结构及其控制策略具有重要的现实意义[26,27],不仅可以加强谐波治理、优化电能质量,还可以提高系统的可靠性和稳定性,有利于其健康发展。但并网逆变器控制技术也存在诸多亟需解决的问题,如研究解决并联并网逆变器的环流问题,研究集各种逆变技术的复合式控制技术以提高并网电能质量,研究对称情况与非对称情况下并网逆变器的统一控制问题以适用于不同的供电场景等。并网逆变器控制技术拥有广阔的发展前景,未来的控制系统必将模块化、高效化、智能化以充分提高分布式电源并网运行的安全性和可靠性,体现分布式电源对电网的强大支撑作用。
[1] Kramer W,Chakraborty S,Kroposki B,et al.Advanced power electronic interfaces for distributed energy systems[R].Battelle:Midwest Research Institute,2008.
[2] 崔金兰,刘天琪(Cui Jinlan,Liu Tianqi).分布式发电技术及其并网问题研究综述(Distributed generation and its grid interconnection issue)[J].现代电力(Modem Electric Power),2007,24(3):53-57.
[3] 丁明,王敏(Ding Ming,Wang Min).分布式发电技术(Distributed generation technology)[J].电力自动化设备(Electric Power Automation Equipment),2004,24(7):31-36.
[4] 刘凤君.现代逆变技术及应用[M].北京:电子工业出版社,2006.
[5] 刘凤君.正弦波逆变器[M].北京:科学出版社,2002.
[6] 王兆安,黄俊.电力电子技术[M].北京:机械工业出版社,2000.
[7] 徐德鸿.电力电子系统建模及控制[M].北京:机械工业出版社,2005.
[8] Timbus A V,Teodorescu R,Blaabjerg F,et al.Linear and nonlinear control of distributed power generation systems[C]∥IEEE Industry Applications Conference,Tampa,USA:2006.
[9] Blaabjerg Frede,Teodorescu Remus,Liserre Marco,et al.Overview of control and grid synchronization for distributed power generation systems [J].IEEE Trans on Industrial Electronics,2006,53(5):1398-1409.
[10] Kim Seul-Ki,Jeon Jin-Hong,Cho Chang-Hee,et al.Modeling and simulation of a grid-connected PV generation system for electromagnetic transient analysis[J].Solar Energy,2009,83(5):664-678.
[11] Wang C,Nehrir M,Gao H.Control of PEM fuel cell distributed generation systems [J].IEEE Trans on Energy Conversion,2006,21(2):586-595.
[12] Wang C.Modeling and Control of Hybrid Wind Photovoltaic Fuel Cell Distributed Generation Systems[D].Montana:Montana State University,2006.
[13]Bertani A,Bossi C,Fornari F,et al.A microturbine generation system for grid connected and islanding operation[C]∥IEEE PES Power Systems Conference &Exposition,New York,USA:2004.
[14]De Brabandere K,Vanthournout K,Driesen J,et al.Control of microgrids[C]∥IEEE Power Engineering Society General Meeting,Tampa,USA:2007.
[15]Borup U,Blaabjerg F,Enjeti P N.Sharing of nonlinear load in parallel-connected three-phase converters[J].IEEE Trans on Industry Applications,2001,37(6):1817-1823.
[16]Piagi P,Lasseter R H.Autonomous control of microgrids[C]∥IEEE Power Engineering Society General Meeting,Montreal,Canada:2006.
[17]Guerrero Josep M,de Vicuna Luis Garcia,Matas Jose,et al.A wireless controller to enhance dynamic performance of parallel inverters in distributed generation system[J].IEEE Trans on Power Electronics,2004,19(5):1205-1213.
[18]Guerrero J M,Matas J,de Vicuna L G,et al.Wireless-control strategy for parallel operation of distributed-generation inverters[J].IEEE Trans on Industrial Electronics,2006,53(5):1461-1470.
[19] Laaksonen H,Saari P,Komulainen R.Voltage and frequency control of inverter based weak LV network microgrid[C]∥ International Conference on Future Power Systems,Amsterdam,Netherlands:2005.
[20]Teodorescu R,Blaabjerg F,Liserre M,et al.Proportional-resonant controllers and filters for grid-connected voltage-source converters[J].Electric Power Applications,2006,153(5):750-762.
[21]Teodorescu R,Blaabjerg F,Borup U,et al.A new control structure for grid-connected LCL PV inverters with zero steady-state error and selective harmonic compensation[C]∥ Nineteenth Annual IEEE Applied Power Electronics Conference and Exposition,Anaheim,USA:2004.
[22]Twining E,Holmes D G.Grid current regulation of a three-phase voltage source inverter with an LCL input filter[J].IEEE Trans on Power Electronics,2003,18(3):888-895.
[23] Hornik T,Zhong Q -C.Control of grid-connected DC-AC converters in distributed generation:experimental comparison of different schemes[C]∥Compatibility and Power Electronics 6th International Conference,Badajoz,Spain:2009.
[24] Timbus A,Liserre M,Teodorescu R,et al.Evaluation of current controllers for distributed power generation systems[J].IEEE Trans on Power Electron-ics,2009,24(3):654-664.
[25]Timbus A V,Teodorescu R,Blaabjerg F,et al.Independent synchronization and control of three phase grid converters[C]∥ International Symposium on Power Electronics,Electrical Drives,Automation and Motion,Taormina,Italy:2006.
[26] 王志群,朱守真,周双喜,等 (Wang Zhiqun,Zhu Shouzhen,Zhou Shuangxi,et al).分布式发电接入位置和注入容量限制的研究(Study on location and penetration of distributed generations)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2005,17(1):53-58.
[27] 王敏,丁明(Wang Min,Ding Ming).含分布式电源的配电系统规划(Distribution network planning including distributed generation)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2004,16(6):5-8,23.
