基于Prony算法的次同步谐振检测方法

董青迅，李兴源，穆子龙，顾 威

（四川大学电气信息学院，成都610065）

现代电力系统的安全问题已经受到愈来愈多的 关 注， 次 同 步 谐 振 SSR（sub－synchronous resonance）是威胁电力系统安全的重要故障之一，它极易造成汽轮发电机组的大轴损毁［1］，所以如何对次同步谐振进行有效准确的检测显得尤其重要。

现有的次同步谐振监测方法按测量信号的不同分为机械量测量和电气量测量两种测量方法。基于机械量测量的次同步谐振监测装置通常是通过在发电机轴系两端装设齿轮片的方法实现。这种方法的原理是利用电磁感应原理快速测量轴系的瞬时速度和轴系的机械位移偏差，从而判断是否发生了次同步谐振［2］。

基于电气量测量的次同步谐振监测可以只测量三相瞬时电流值。测量信号经过滤波处理，得到其中的次同步频段信号，将它和整定值比较，就可以做出逻辑判断，经延时电路以决定是否应该做出报警或者动作于保护。这种基于电气量测量的检测方法结构简单，价格便宜，可靠性高，便于维护［3］。由于次同步谐振电流在三相瞬时电流中所占的比率相对很小，加上测量的瞬时电流中不可避免的含有噪声，因此如何从含有噪声的三相电流的瞬时检测信号中，有效滤出这些次同步分量信号是采用该方法的一个重要问题，对信号的滤波和处理都有非常高的要求［4］。

本文提出一种基于Prony算法的次同步谐振检测方法。选取瞬时电流作为测量信号，对滤波后的信号利用Prony算法进行分析，辨识出次同步分量的幅值，观察其在连续时间段上的变化规律，快速准确的判定次同步谐振的发生，以便及时采取抑制措施。

1 次同步谐振的信号特征

电网的互补自然频率接近汽轮发电机轴系的一个扭转频率时，可能激励次同步谐振，在这种条件下，由于转子振荡感应的小电压可以产生大的次同步电流，该电流产生转子扭矩的振荡分量，加剧转子振荡，当该扭矩大于机械阻尼时，耦合的机电系统会经受增长的振荡［5］。

由以上分析可知：首先，次同步电流是由转子振荡感应出来的，因此它具有和次同步谐振相同的频率；其次，转子振荡的加剧，将感应出更大的次同步电流，后者会产生更大的转子扭矩振荡分量，进一步加剧转子振荡，因此次同步电流的幅值变化趋势可以表征次同步谐振的振荡趋势。基于上述两点，再考虑到尽管扭矩振荡加剧是次同步谐振发生的重要判据［6］，但直接提取扭矩往往比较困难，相反电流量是最直观最易获取的量，因此只要能从采样电流信号中滤出其中的次同步频段信号，就可以更加有效、实时地监测次同步谐振。

本文就是要从瞬时采样电流信号入手，经过Prony分析，辨识出其中次同步频段信号的幅值，提出一种新的判据。

2 基于Prony算法的次同步谐振检测方法

2.1 Prony算法概述

1975年，Gaspard Riche，Baron de Prony提出Prony方法，该方法使用指数函数的一个线性组合来描述等间距采样数据的数学模型，然后经过适当扩充，形成了能够估算给定信号的频率、衰减因子、幅值和初相位的算法［7］。

近年来，Prony算法在电力系统分析与控制领域得到了广泛的应用［8～12］。大部分的研究工作集中在两方面：一是研究应用Prony算法分析振荡数据，提取振荡特征；二是利用Prony算法对系统进行辩识，得出系统模型或参数。

上述研究结果表明，在电力系统的研究中，Prony分析方法有广泛的适用性，特别是在小信号稳定控制领域的系统辨识中的优势十分明显［13］。利用Prony分析实测数据得到的信息比小扰动分析得到的信息更准确［14］。

2.2 Prony算法的实现步骤［15］

假设按等时间间隔Δt进行采样的N 个数据点，可由p个指数函数的线性组合模拟，即

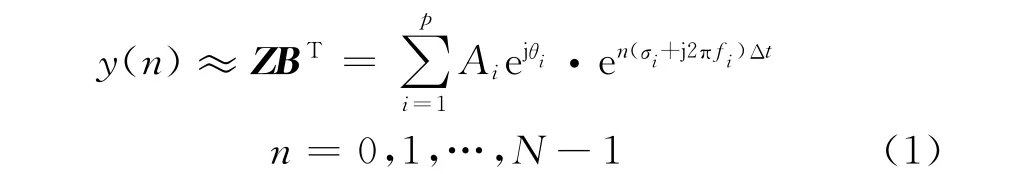
其中：y（n）为第n个采样点；Z＝ ［z1，z2，…，zp］为极点；B＝ ［b1，b2，…，bp］为相应留数；Ai为幅值，θi为初相位，σi为衰减因子，fi为频率。

Prony辨识算法的计算步骤简介如下。

利用采样数据点构造矩阵Y，并求解方程组：

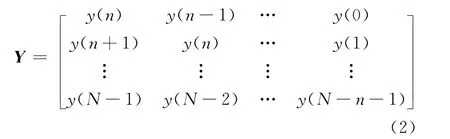
令

其中，A＝ ［1，a1，a2，…，ap］。当N ＞2p时，A为方程组的最小二乘解。

求解由系数a1，a2，…，ap构成的多项式（4），该多项式的根即为Prony辨识出的p个极点：

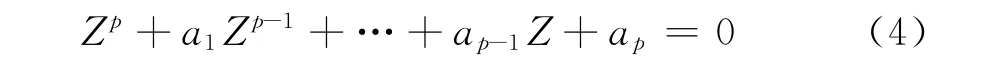
进一步利用最小二乘求解方程组（5），以获取留数B：

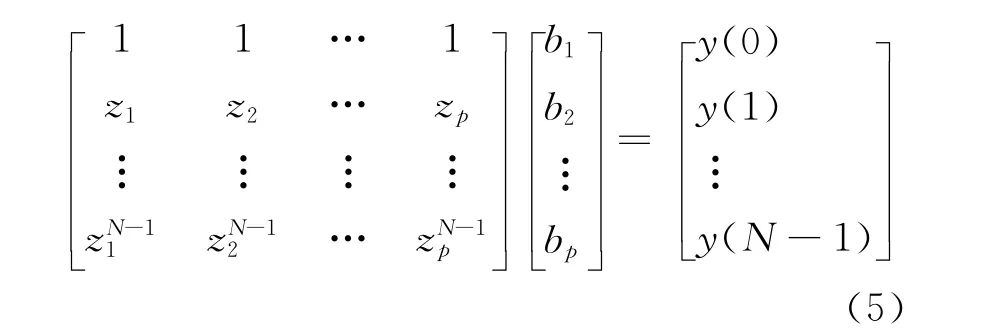
利用式（3）、（4）和式（5）计算结果，由式（6）计算出式（1）中模拟输入信号的线性组合的振幅、相位、衰减因子、频率各量：

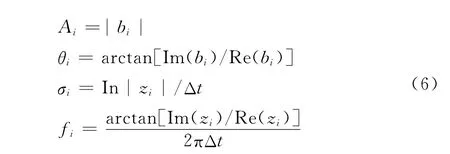
本文中，该算法基于Matlab软件编程实现。

2.3 基于Prony算法的次同步谐振检测原理

利用Prony辨识不需要列写大规模的系统方程和建立系统的详细模型，避免了求解大规模矩阵的特征根这一难题。同时，利用该方法还可直接获取给定信号的频率、衰减因子、幅值和初相位，这就为在复杂系统中检测出次同步谐振提供了一条较好的途径。因此，基于Prony算法的SSR检测原理如下：正常运行状态下，次同步频段没有信号，利用Prony辨识出来的幅值为零。发生次同步谐振时，会在电流波形中叠加次同步分量，此时有两种情况，一种是增幅振荡，另一种是振荡衰减。前者随着次同步谐振影响的加强，表现是次同步频段下的信号振荡加剧，幅值增大且不回落；后者次同步频段信号先振荡加剧，幅值增大，在次同步谐振衰减时，次同步分量也逐渐衰减，所以表现为随后幅值减小。综上，该方法的检测原理即是利用Prony算法辨识出次同步分量的幅值，将其幅值的不断增大作为发生次同步谐振的判定依据。

3 仿真验证

3.1 基于Prony算法的次同步谐振检测

利用Matlab和电磁暂态仿真软件PSCAD对该方法进行验证。采用IEEE第一标准测试系统作为仿真模型，如图1所示。

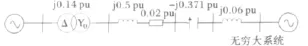
图1 IEEE第一标准测试系统Fig.1 IEEE first benchmark system model

设电流信号基频为50Hz，幅值为50A，相位为0，次同步分量位于两个频段，分别是频率为40 Hz、幅值为15A、相位为2π／3；频率为20Hz、幅值为15A、初相位为2π／3。

由于Prony算法对噪声十分敏感，仅靠Prony算法本身包含的最小二乘估计也很难完全或较大地消除噪声的影响，噪声的存在将会极大地影响次同步谐振分析的精度，所以需要对输入数据先进行滤噪处理。本文采用卡尔曼滤波器首先对输入数据进行预处理，再利用Prony算法进行分析。

设故障发生在5.0s，持续0.075s。以6s作为采样起点，采样频率为1000Hz，采样时间0.32s，采样出的电流信号如图2所示。首先通过卡尔曼滤波器得到滤波后的信号，见图3，之后利用Prony算法进行分析，图4给出了以通过卡尔曼滤波器滤波后的采样信号为输入信号的Prony分析的逼近结果。由图4可见，经过卡尔曼滤波后的Prony分析可以十分精确地逼近实际振荡曲线。

图2 采样区间的电流信号Fig.2 Current signal of the sampling interval

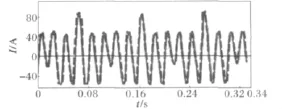
图3 经过滤波处理后的电流信号Fig.3 Current signal after filtering

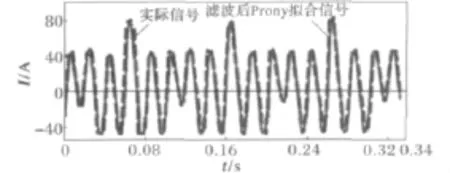
图4 实际信号和滤波后Prony拟合信号Fig.4 Actual signal and the Prony fitting signal

表1是以经过卡尔曼滤波后的信号为输入的Prony分析结果。

表1 采样电流信号prony辨识结果Tab.1 Prony identification results of the sampling current signal

由表1可见，次同步频段信号的振荡幅值不仅没有衰减，反而有略微增大的趋势，可以判断此运行方式下该系统发生了次同步谐振。

3.2 发电机暂态力矩仿真分析

为验证上述分析方法的正确性，采用传统的发电机暂态力矩仿真分析方法与之进行对照。图5给出发电机质块与励磁机质块连接轴的扭振转矩。

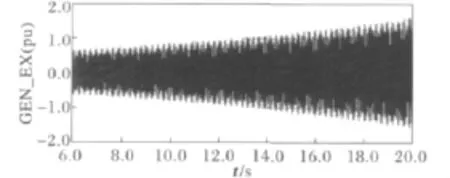
图5 发电机质块与励磁机质块连接轴的扭振转矩Fig.5 Torque of the connecting shaft between generator module and exciter module

很明显，质块之间的扭矩出现了明显的放大现象，整个系统出现严重的次同步谐振现象。将提出的基于Prony算法的次同步谐振检测方法与发电机暂态力矩仿真分析方法进行对照，两种方法得出的结论（此运行方式下系统将发生次同步谐振）是一致的，这也验证了前者的正确性。

3.3 性能优势

（1）基于prony算法的次同步谐振检测方法更加全面地反映次同步谐振。基于Prony算法的次同步谐振检测方法可以得出系统谐振频率、谐振幅值等有关次同步谐振机理更为有效的信息，这一点相比基于人工神经网络的SSR检测方法具有明显优势。

（2）该方法极强的实时性。检测只需要很短的采样数据和Matlab极快的运算分析速度是该方法具有极强实时性的根本原因。与普遍采用的基于小波分析的次同步谐振检测方法做一个对比，依然针对本例。用小波分析得到的次同步频段信号如图6所示。

图6 基于小波变换的次同步谐振分量的提取Fig.6 Extraction of the torsional oscillation component with wavelet transform

观察次同步谐振分量的振荡趋势同样可以判断此运行方式下系统将发生次同步谐振，但基于Prony算法的次同步谐振检测方法避免了小波变换在应用时存在的合理选择匹配小波基的困难，因此在线监测过程可以节省更多时间，保证可靠性的同时，更出色的满足了实时性的需求。

4 结语

基于Prony算法的次同步谐振检测方法首先采用卡尔曼滤波器对输入数据进行预处理，再利用Prony算法进行分析。依据辨识结果，观察连续时间段上次同步频段信号的幅值变化，进而判定是否发生次同步谐振。算例结果表明，经过滤波后的Prony分析可以十分精确地逼近实际振荡曲线，通过观察辨识出的次同步分量的幅值变化规律，能准确地检测出次同步谐振，从而证明了该方法的有效性和实用性。

［1］ IEEE Subsynchronous Resonance Working Group.Countermeasures to subsynchronous resonance problems［J］.IEEE Trans on Power Apparatus and Systems，1980，99（5）：1810－1818.

［2］ 程时杰，曹一家，江全元.电力系统次同步谐振的理论与方法［M］.北京：科学出版社，2009.

［3］ IEEE Subsynchronous Resonance Working Group.Reader＇s guide to subsynchronous resonance［J］.IEEE Trans on Power Systems，1992，7（1）：150－157.

［4］ Bowler Colin E J，Baker Daniel H，Mincer N A，et al.Operation and test of the Navajo SSR protective equipment［J］.IEEE Trans on Power Apparatus and Systems，1978，97（4）：1030－1035.

［5］ Prabha Kundur.电力系统稳定与控制［M］.北京：中国电力出版社，2002.

［6］ 李兴源.高压直流输电系统的运行和控制［M］.北京：科学出版社，1998.

［7］ Grund C E，Paserba J J，Hauer J F，et al.Comparison of Prony and eigen analysis for power system control design［J］.IEEE Trans on Power Systems，1993，8（3）：964－971.

［8］ 刘红超，李兴源（Liu Hongchao，Li Xingyuan）.基于PRONY辨识的交直流并联输电系统直流阻尼控制的 研 究 （Study of DC damping control in AC／DC transmission systems based on Prony method）［J］.中国电机工程学报（Proceeding of the CSEE），2002，22（7）：54－57.

［9］ 刘红超，李兴源，邱小燕，等（Liu Hongchao，Li Xingyuan，Qiu Xiaoyan，et al）.基于Prony算法的HVDC输电系统模型辨识（A model identification method of HVDC transmission systems based on Prony analysis）［J］.四川大学学报：工程科学版（Journal of Sichuan University：Engineering Science Edition），2004，36（2）：86－89.

［10］ 苏小林 ，周双喜（Su Xiaolin，Zhou Shuangxi）.Prony法在同步发电机参数辨识中应用（Application of Prony method to parameter identification of synchronous generators）［J］.电 力 自 动 化 设 备 （Electric Power Automation Equipment），2006，26（9）：1－4.

［11］ 魏伟 ，赵书强 ，马燕峰（Wei Wei，Zhao Shuqiang，Ma Yanfeng）.基于Prony算法的模糊电力系统稳定器设 计 （Design of fuzzy power system stabilizer based on Prony algorithm）［J］.电力自动化设备（Electric Power Automation Equipment），2005，25（3）：54－59.

［12］ 管秀鹏 ，程林 ，孙元章 ，等（Guan Xiupeng，Cheng Lin，Sun Yuanzhang，et al）.基于Prony方法的大型互联电网PSS参数优化设计（PSS parameter optimization on large－scale interconnection power grid based on Prony method）［J］.电力系统自动化（Automation of Electric Power Systems），2006，30（12）：7－11.

［13］张贤达.现代信号处理［M］.北京：清华大学出版社，2002.

［14］Johnson M A，Zarafonitis I P，Calligaris M.Prony analysis and power system stability some recent theoretical and applications research［C］∥IEEE Power Engineering Society Transmission and Distribution Conference，Seattle，USA：2000.

［15］ 赵成勇，刘娟（Zhao Chengyong，Liu Juan）.Prony算法在电力系统暂态信号分析中的应用（Analysis of power system transient signal based on Prony algorithm）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2008，20（2）：60－64.