水终端在用于高压电缆试验时串联谐振系统Q值的理论分析

范玉军， 吴长顺

(上海电缆研究所，上海200093)

水终端在用于高压电缆试验时串联谐振系统Q值的理论分析

范玉军， 吴长顺

(上海电缆研究所，上海200093)

介绍了在用串联谐振系统及水终端进行电缆高压试验时，利用理论公式以及Matlab软件分析各个参量对系统Q值的影响。为电缆进行高压试验时充分有效地利用串联谐振系统奠定了理论基础。

高压电缆；串联谐振系统；Q值；水终端；Matlab

0 引 言

根据国家标准GB/T 11017、GB/Z 18890和GB/T 22078的例行和型式试验要求，要对110 kV及以上电压等级的高压电缆进行耐压和局放试验。目前针对电缆的高压试验一般采用脱离子水终端作为试验终端，采用串联谐振系统为高压电源。选用水终端作为高压电缆试验终端的原因是其具有操作方便、良好的电场均化效果以及干净无污染等优点，即通过调节水的电导率和流速可以使终端的电场分布得到优化而不致产生放电，因此可以满足局放、耐压以及冲击试验等要求。采用串联谐振电源系统的原因是利用串联谐振的原理既可满足试验要求，又可以减小设备容量和占地空间，从而减少投资成本。

在利用串联谐振电源系统时，尤其是有水终端存在的情况下，如果不能满足谐振条件或者谐振后品质因数Q值太低，都可能无法达到标准规定的试验电压而导致试验无法进行，因此系统能否谐振以及谐振后Q值大小是决定试验能否进行的关键。为此有必要对影响串联谐振系统Q值的各个因素从原理上进行分析，为利用串联谐振电源系统进行电缆的高压试验奠定理论基础。

1 谐振条件和Q值的理论推导

利用串联谐振系统和水终端对高压电缆进行试验时，其试验回路如图1所示。

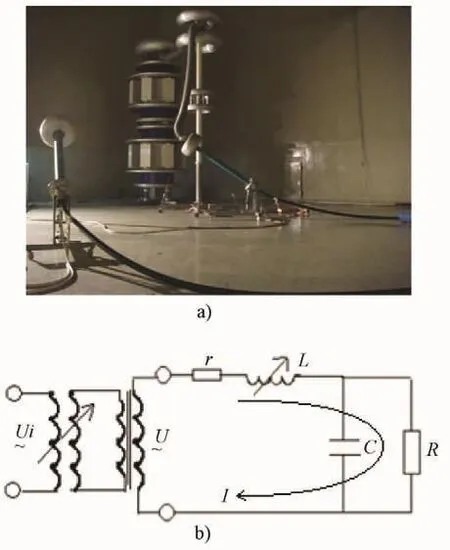
图1 电缆高压试验的现场图片和等效电路图

在等效电路中，U为励磁变压器的输出电压，r是主回路中的等效内阻，L是电抗器中电感值，其阻抗以Z1表示，C和R并联构成样品的等效阻抗Zx，其中样品包括电缆和试验终端以及高压分压器。因此在主回路中总的阻抗Zz可以用式(1)表示：

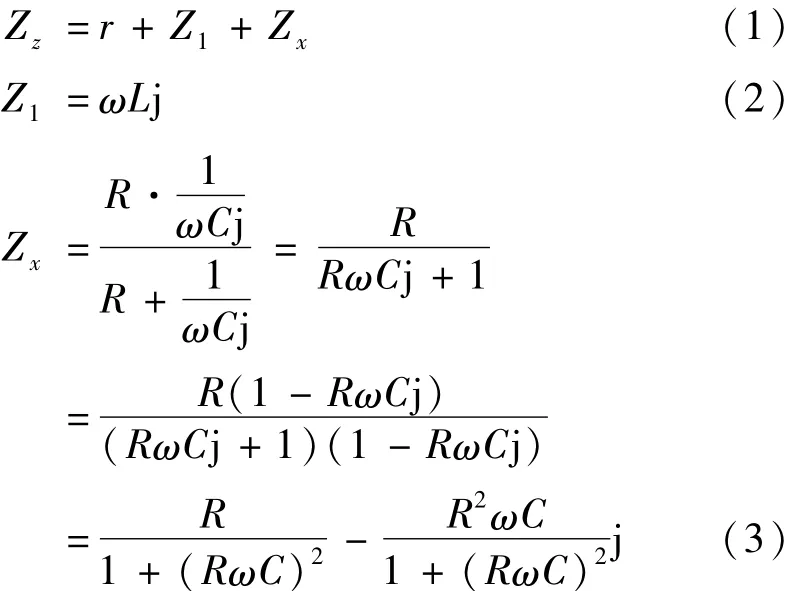
将式(2)和式(3)代入式(1)，

通常Q值为试品两端的电压与励磁变压器所输出电压的比值，也即Zx与Zz的模值之比值：

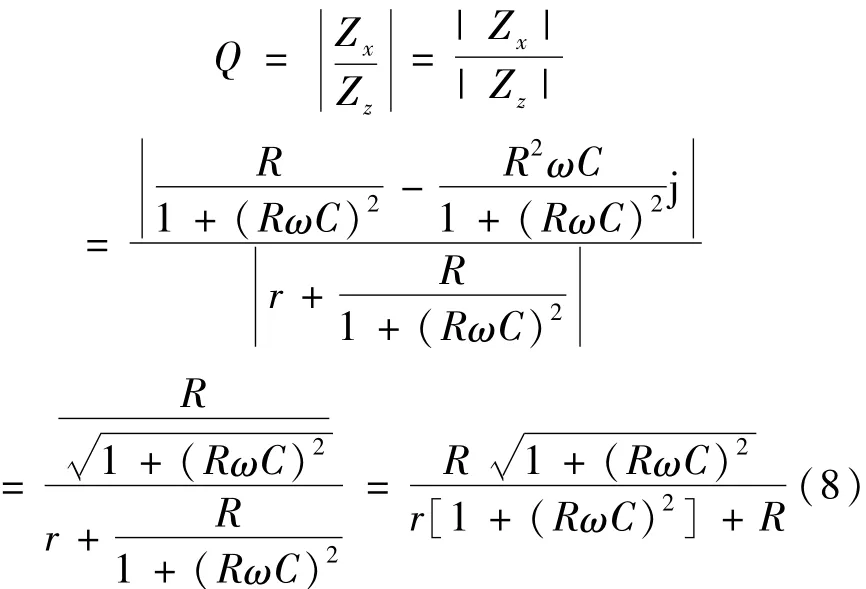
结合谐振条件

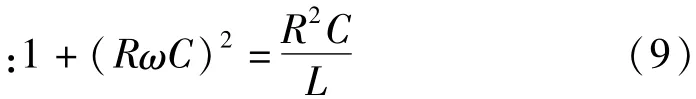
所以

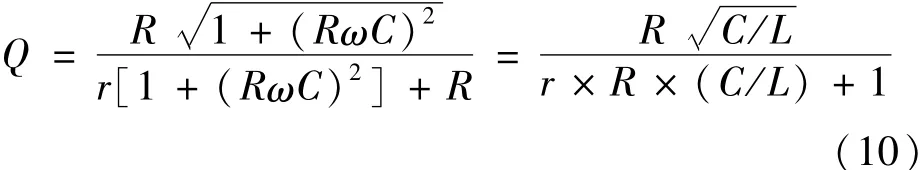
式(6)和式(10)即在一般条件下串联谐振系统中的谐振条件和Q值表达式。通常情况下，电缆的绝缘电阻值较大，尤其是中高压电缆阻值一般在1014Ω以上，如果不考虑试验终端对阻值的影响，则可以对式(6)和式(10)进行简化。即当R足够大时，在式(6)中，由于R≫1，则(RωC)2≫1，所以谐振条件变成了：

即 ωL=1/(ωC)

同理在式(10)中，由于R≫1，则r×R×(C/L)≫1，r×R×(C/L)+1≈r×R×(C/L)，此时式(10)可以简化成：

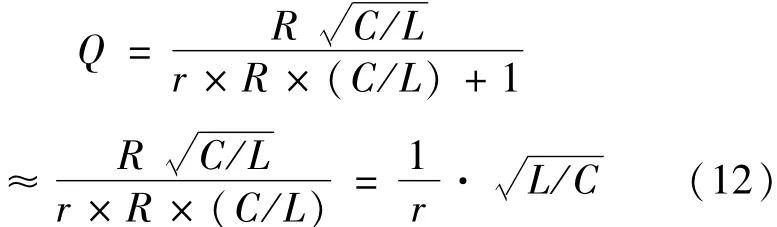
式(11)和式(12)也是通常串联谐振系统中被大家所熟知的谐振条件和Q值表达式。

2 谐振时L-C关系及各个参数对Q值的影响程度

为了进一步明确谐振条件以及谐振时各个参数对Q值的影响，绘制不同负载电阻情况下的L-C曲线和Q-C曲线，以便更直观地了解谐振条件及相关参数对Q值的影响程度。从式(6)和式(10)可以看出谐振条件(L-C)以及Q值与电容的关系(Q-C)并非典型函数关系式，因此可以利用数学软件Matlab来绘制其关系曲线。

以一台1 200 kV的串联谐振系统和750 kV的脱离子水终端为例，来说明相关参数对Q值的影响。在此系统中，其主回路中的内阻r=1 161Ω(若忽略温升的影响，一台串联谐振系统的等效内阻r是恒定的)，水终端两电极之间的绝缘电阻R(实为水终端和电缆电阻的并联)的范围为1～8 MΩ，取决于脱离子水的电导率。现选取R值为1 MΩ、8 MΩ和∞三种情况来分析L-C及Q-C曲线关系，其中R值为∞时相当于式(11)和式(12)的情况。

首先利用Matlab中plot函数来绘制谐振条件下的L-C曲线(见图2)，图中横轴代表负载电容，取值是从200～10 000 pF(核算成高压电缆长度约为1～500 m)，步长取200 pF。纵轴代表与之匹配的电感值，从中可以看出：

(1)R=∞时，L-C之间的关系为反比例递减关系;

(2)R=1 MΩ和R=8 MΩ两条曲线形状类似，L值随负载电容的增大，先增后减。两条曲线相比，前者较为平滑，峰值出现较晚，且 L值始终低于后者;

(3)过了峰值后，随着负载电容的继续增大，所有曲线的L值无限地接近。

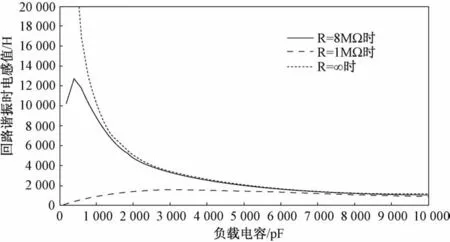
图2 谐振时负载电阻不同情况下的L-C关系曲线

接下来再利用Matlab中plot函数来绘制谐振条件下的Q-C曲线(见图3)，横轴代表负载电容，取值是从200～500 000 pF，核算成高压电缆长度约为1～25 000 m，为了描绘出各自曲线的完整趋势，在L-C和Q-C两种关系图中对C值的取值范围有所不同，步长取200 pF。纵轴代表谐振时的Q值。从中可以看出：

(1)R=∞时，Q-C之间的关系为反比例递减关系;

(2)R=1 MΩ和R=8 MΩ两条曲线形状类似，Q值随负载电容的增大，先增后减。两条曲线相比，前者较为平滑，峰值出现较晚，且Q值始终低于后者;

(3)过了峰值后，随着负载电容的继续增大，所有曲线的Q值无限地接近;

谐振条件下，L-C与Q-C曲线形状类似，R=∞时两种曲线都是反比例的递减关系，除R=∞以外曲线都是先增后减。不同点是L-C曲线的峰值出现较早，在3 000 pF以内即出现了峰值，而Q-C曲线的峰值则在100 000 pF以内出现。

图3 谐振时负载电阻不同情况下的Q-C关系曲线

3 结束语

高压交联电缆试验时，样品的长度从十几米到几千米不等，有时要对样品进行耐压裕度试验，电压的幅值要达到700 kV甚至更高，因此水终端和串联谐振系统的配合使用是不可或缺的。而如何选择设备、如何调节各个参数以满足试验要求是关键。有本文的理论分析和所举实例作为基础，在遇到具体试验问题时，可以结合实际参数进行计算。

Theoretical Analysis to Q Value of Series Resonance Power during Test for HV Cable w ith W ater Term ination

FAN Yu-jun，WU Chang-shun
(Shanghai Electric Cable Research Institute，Shanghai200093，China)

The relations between Q value of series resonance power and different correlative parameters are analyzed with theoretical formulas and Matlab when high voltage testing to cablewith series resonance power and water termination.The treatise lays the theoretic foundation for series resonance power being used fully and effectively to cable high voltage test.

high voltage cable;series resonance power;Q value;water termination;Matlab

TM206

A

1672-6901(2012)05-0036-03

2012-04-24

范玉军(1979-)，男，工程师.

作者地址:上海市军工路1000号[200093].