基于遗传算法的后勤运输车路径规划

张 亮，周继宝

(1.沈阳理工大学 汽车学院，沈阳 110168;2.第二炮兵士官学校 501 教研室，山东 潍坊 262500)

军事后勤保障主要指在战时或平时军用物资的筹措、储存、运输和流通等过程，是军事战略战术中重要的组成部分。现代信息化战争对后勤保障提出了准确、快速的要求，如何建立科学有效的后勤配送运输体系对于提高后勤物资和作战物资配送速度、节约军费开支等均具有重要的意义。

后勤运输车的路径优化问题是后勤运输体系中的重要组成部分，主要是指如何设计一条配送路径，使运输车从出发点将物资成功运送至各个需求点，实现行驶里程最短。本文针对此问题展开研究，将遗传算法引入到优化过程中，以实现配送车辆路径选取的最优决策。

1 后勤配送系统分析

后勤运输车辆配送路线的合理优化既能够提高后勤运输保障效能，又能保持运输保障与作战部队的保障需求协调一致，是当代信息化战争不容忽视的技术性环节之一，具有重要的理论意义和使用价值，主要体现在以下方面:

1)优化战略物资运输路线，可以提高运输效率，实现整体战略补给速度最优化，提高后勤保障能力。

2)可以准时、快速地把战略物资送到相应的部队所在地，从而潜在地提高部队作战效能。

3)合理的优化可以使后勤运输车辆的配送任务完成得更为精确。

4)可以节约运输成本，节省费用开支。

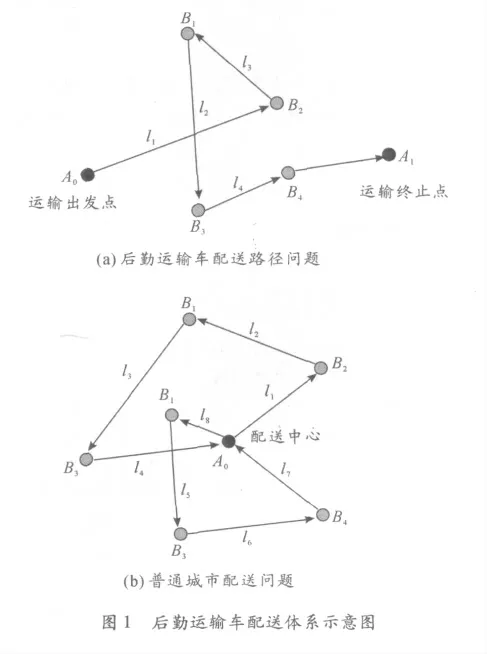
后勤运输车配送过程需要将军用物资或补给从配送出发点逐次送往战略基地，即接收点。与一般城市配送不同，战略后勤运输车在配送任务结束后需要将配送车辆开至指定位置而非返回原点，如图1 所示。

配送路线的优化从数学的角度属于NP-hard 问题，随着节点数量增多的呈现维数灾现象，因此传统的枚举法往往并不适用。另外在实时战略实施过程中，优化算法必须要求时效性和通用性，能够实现路径选取方案的动态优化管理［1-3］。

2 数学建模

2.1 输入与输出

为了便于对后勤运输车配送优化问题进行研究，首先建立数学模型。模型的输入为已知的各个需求点的地理位置，可以用各个需求点及运输起始点的距离矩阵描述，如式(1)所示。

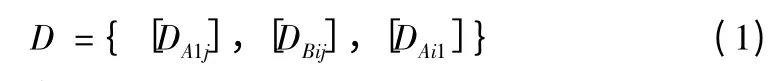
其中D 为距离矩阵。

优化模型的输出是一系列车辆路径的选取决策的集合，即

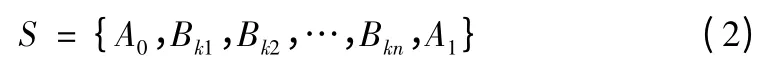
其中:n 为需求点的数目;A0为运输起始点;A1为运输终止点;Bki为第i 个需求点。

2.2 目标函数

后勤运输车配送路线优化问题的优化目标是使配送任务在尽可能短的时间内完成。假设车辆行驶速度为定值，则所耗费的时间与行驶里程呈正比，根据输入条件的形式，总的行驶里程在建模过程中可以分为3 部分进行计算，即从出发点至第1 个需求点的路径长度，遍历所有需求点的路径长度和最后一个需求点至运输终止点的路径。优化数学模型的目标函数为

其中:λD为总的运输路线行驶里程;d(·)为距离算子;Bx为从出发点配送至的第1 个需求点;By为到达终止点前的最后一个需求点。

2.3 约束条件

每辆后勤运输车配送至所有需求点的过程中所能携带的货物量存在一个上限，且配送时间不能超过最大时间上限，因此约束条件可以如式(4)、(5)所示进行描述。

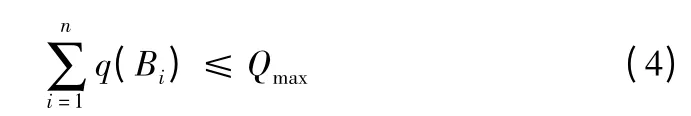
其中:Qmax为每辆配送车辆的载运上限值;q(·)为需求量计算因子。

其中:v 为平均车速;T 为配送任务所要求的最大时间限度;α 为因装卸所产生的时间修正因子。

2.4 优化模型

优化问题的求解是根据输入条件与目标函数，确定最优的路径解决方案，并满足约束条件。根据上述分析过程，可以将后勤运输车从出发点向各个战略需求点进行配送并最终抵达终止点的路径寻优问题的优化模型如式(6)所示进行描述。

3 基于遗传算法的优化方案

遗传算法具有潜在的并行寻优特性和不依赖于梯度信息的特点，因此广泛应用于诸多优化领域，可以处理传统搜索方法难以解决复杂非线性优化问题［4-5］。

本文采用遗传算法来进行后勤运输车配送路线的优化。首先将遗传算法基本参数设定如下:

种群大小M=20

最大代数G=100

交叉概率Pc=1.0

变异概率Pm=0.1

基于遗传算法的后勤运输车配送路线优化的具体实施步骤如图2 所示。

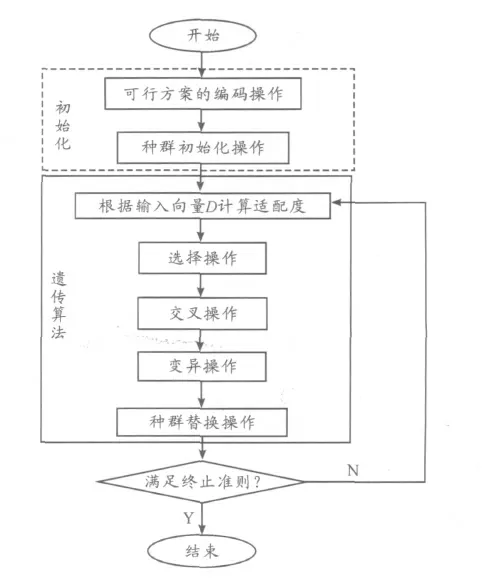
图2 基于遗传算法的车辆路径优化流程

在设定参数完成之后，对可行解空间进行遗传编码操作，并生产初始种群，设定适配度函数与遗传算法终止条件。

3.1 编码规则

遗传算法编码的方案通常有二进制编码和浮点数编码2种。针对后勤运输车配送路径优化问题的特点，采用十进制浮点数编码方案，使用各个需求点的节点编号作为基因来组成染色体，例如对于染色体:

其对应的表现型为:

3.2 适配度函数

适配度函数是根据优化问题的数学模型中的目标函数转化而来，如式(7)所示定义。

其中:dδs与dδe分别为路径中第1 路段与最后路段的长度，к1～кn表示由可行解的编码所决定的配送节点顺序。

3.3 遗传算子设计

主要包括选择算子、交叉算子和变异算子的设计。选择算子的设计方案采用经典的排序法，即根据染色体计算所得的适配度函数来进行排序操作，根据适配度值来选择排序靠前的10个染色体作为选择结果。

交叉操作采用单点交叉，对于选定的2 个父代个体随机地选取第t 个基因处为交叉点，首先将父辈X1中的前t 个基因作为子代个体的前t 个基因，然后将第2 个父辈染色体X2的后n-t 个基因依据第2 个父辈染色体中的顺序构成子代，见图3。

图3 交叉操作示意图

变异操作采用逆位变异，即针对变异染色体的随机选取的变异位s，使其与n -s 位进行对换，从而生成新的染色体，如式(8)所示。

3.4 终止条件的设计

求解从后勤运输车配送路径优化问题时，如果以下任一条件满足时，则遗传算法终止并输出所记录的最优解。

1)优化过程中得到的全局最优解在连续10 次迭代中都没有被改进;

2)达到最大迭代次数次100 次。

4 优化结果分析

基于所设计的遗传算法进行后勤运输车配送路径优化问题研究。假设从出发点到终止点之间共有7 个节点，初始条件为:

其中:D0为需求节点之间的距离矩阵;D1为从出发点至各节点的距离信息;D2为各节点至终止点的距离信息。

对于任意染色体X 适配度函数的计算实例如图4 所示。

采用谢菲尔德Matlab 遗传算法工具箱函数来进行算法实现。选择算子采用select( )函数，交叉算子采用xovshrs( )函数，变异算子采用mutate( )函数，经过42 次迭代后算法收敛至最优解

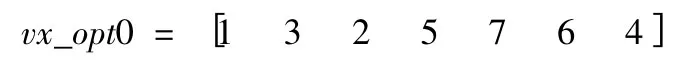
对应的表现型，即最优配送路径见图5。

5 结束语

本文采用遗传算法对后勤运输车的路径优化问题进行了研究，设计了遗传编码、适配度函数和遗传算子等，并基于谢菲尔德Matlab 遗传算法工具箱进行了算法实现与仿真，结果表明遗传算法适合于后勤运输路径的寻优，针对相应的需求点分布情况可以迅速做出最优配送路径决策，从而节省运输车行驶里程和运输时间。

［1］祝崇隽，刘民，吴澄.供应链中车辆路径问题的研究进展及前景［J］.计算机集成制造系统，2001，11(7):1 -6.

［2］朗茂祥，胡思继.用混合遗传算法求解物流配送路线优化问题的研究［J］.中国管理科学，2003，2(4):44 -46.

［3］孙小年，陈幼林，杨东援.装卸一体化车辆路径问题的遗传算法研究［J］.系统工程理论与实践，2007(2):33 -35.

［4］郝艳伟，李祖枢.一种改进的遗传规划算法［J］.重庆理工大学学报:自然科学版，2011，25(4):74 -78.

［5］晏刚.基于改进遗传算法的AUV 路径规划［J］.重庆理工大学学报:自然科学版，2010，24(5):81 -85.