涡轴发动机简化实时模型研究

邢耀东，黄金泉，鲁峰，姚文荣

（1.南京航空航天大学能源与动力学院，南京 210016;2.中航工业航空动力控制系统研究所，江苏 无锡 214063）

涡轴发动机简化实时模型研究

邢耀东1，黄金泉1，鲁峰1，姚文荣2

（1.南京航空航天大学能源与动力学院，南京 210016;2.中航工业航空动力控制系统研究所，江苏 无锡 214063）

邢耀东（1986），男，在读硕士研究生，研究方向为航空发动机建模与故障诊断。

>

涡轴发动机数控系统传感器故障诊断需机载的发动机数学模型，由于缺乏部件特性数据，根据某型发动机地面试车稳态数据和动态数据，建立涡轴发动机慢车以上状态简化数学模型。该模型具有较好的实时性，稳态模型采用插值算法，动态模型针对不同参数分别采用动态系数法和转子动力学方法。数值仿真结果表明：该简化模型具有较高的动态和稳态精度，可以满足传感器故障诊断的需求。

涡轴发动机；简化模型；插值算法；动态系数法；转子动力学

0 引言

航空发动机数控系统传感器的稳定可靠，对于保证发动机FADEC系统正常工作至关重要[1-2]。传感器解析余度技术[3]是1种典型的基于模型的传感器故障诊断方法，而机载模型的精度直接影响传感器故障诊断性能[4]。因此，建立准确的发动机模型对于传感器故障诊断具有十分重要的意义。

目前常用的建模方法包括解析法和实验法。解析法建模需要部件特性数据，得到的模型精度较高，能在全包线范围内模拟发动机工作状态，因此在国内外被普遍使用[5-7]。在缺乏部件特性的情况下，可以利用实验法建立发动机简化模型。实验法一般只根据系统输入输出建立模型，而不关心系统内部复杂的机理，常见方法通常有时域分析、频域分析或用统计相关测定法来对系统进行辨识。周文祥采用动态系数法建立了双轴涡扇发动机简化实时模型[8]，冯海峰则利用发动机部件级模型得到发动机工作特性线，采用特性线法建立发动机模型[9]。

本文旨在根据发动机试车数据，采用插值算法、动态系数法和转子动力学方程建立慢车以上状态涡轴发动机简化模型，即根据发动机的试车数据得到发动机稳态工作线，采用插值算法建立发动机稳态模型，采用动态系数法建立发动机动态模型，负载部分则根据转子动力学方程进行求解。涡轴发动机简化模型包括燃气发生器、动力涡轮和负载模型。

1 试验数据预处理

试车数据包括供油量Wf、燃气涡轮转速ng、动力涡轮转速np、燃气涡轮出口温度T45a（由2个传感器测得）及负载杆角度α。另外，还包含压气机出口压力P3、动力涡轮输出功Ne的稳态点数据，环境温度T1、环境压力P1。建模之前应对试车数据进行预处理。

（1）为了使得各组数据具有可比性，首先利用相似原理将其转换为换算参数。

（2）原始数据不可避免地存在测量噪声，在对数据进行分析处理之前，利用origin自带的滤波工具对原始数据进行滤波处理，效果如图1所示。

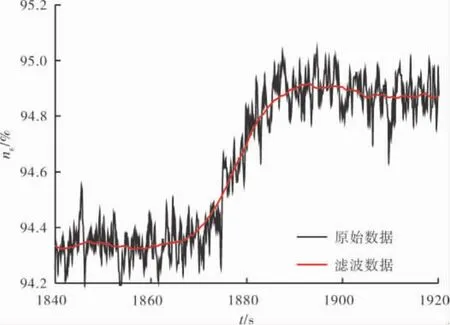
图1 原始数据的滤波处理

（3）T45选择。由于温度场分布不均匀，T45根据2个传感器测量数据确定。根据工程经验，T45选取准则如下：当T45a、T45b的差值在80 K以下时，T45取T45a、T45b的均值；否则取二者之间的较大值。

2 稳态模型建立

动态模型是在发动机稳态工作线的基础上，利用加减速系数建立的，因此发动机稳态时各参数之间的关系是简化模型建模的基础。

（1）稳态数据处理

以ng～Wf为例，其稳态数据取舍如图2所示。在整合稳态工作线时，发现有些点明显偏离稳态工作线的总体趋势(图2中小圈内的点)，通常认为是野点而舍去。为了提高插值计算精度，在缺少试验数据的区段内，根据已有数据拟合多项式曲线，以适当间隔在曲线上选点作为稳态建模所需的工作点。试车数据中的T45、P3、Ne稳态数据的整理与ng的类似。

（2）稳态模型建立

在某型涡轴发动机地面试车时不调节引放气系统和导叶角，也不对叶尖间隙进行控制。在此前提下，由发动机原理可知，给定环境温度、压力，涡轴发动机稳态时的ng、T45、Ne可近似地认为由Wf惟一确定。

根据稳态数据，利用插值算法建立涡轴发动机的稳态模型。发动机各典型参数的计算公式为

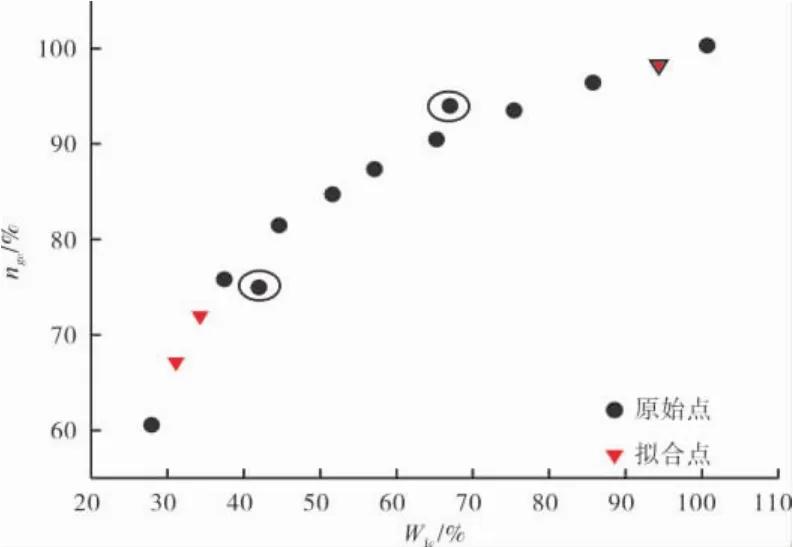
图2 ng～Wf稳态数据取舍

式中：f、ψ、φ为稳态时各参数之间的函数关系；下标c、s分别为换算参数和稳态参数。

3 动态系数法

在发动机稳态工作过程中，每个ngc都对应着1个维持其不变的需求供油量，当实际Wfc与需求供油量不匹配时，ngc就会变化，即发动机进入动态过程。定义某一转速对应的需求油量为

定义此时实际Wfc与Wfcs的差为剩余供油量

因此，当ΔWfc＞0，实际供油量大于需求油量时，燃气涡轮功率大于压气机消耗功率，ngc增大；反之当ΔWfc＜0时，ngc减小。并且ΔWfc越大，ngc变化幅度也越大。由此可见，燃气发生器各状态参数的变化与ΔWfc存在对应关系，可以通过动态系数表示。

定义第i时刻ngc、T45c、Nec的动态系数分别为

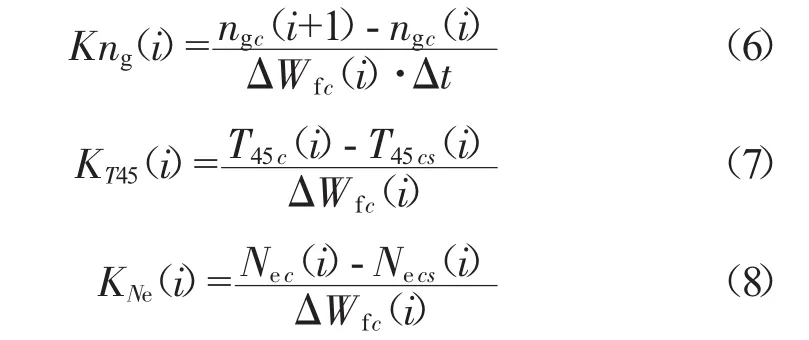
式中：Δt为仿真步长；T45cs、Necs分别由ngc的动态数据，按照式（2）、（3）计算

Kng、KT45、KNe均由试验数据获取，仿真时根据插值函数获得不同ngc的动态系数。

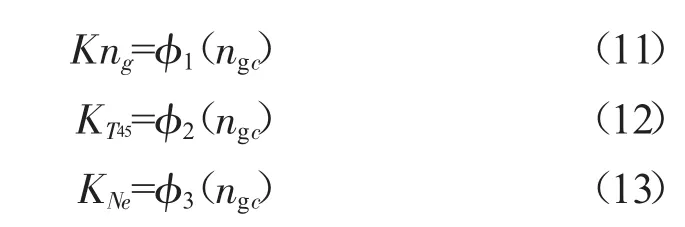
燃气发生器加速和减速过程中动态系数不同，因此需分别计算加速系数和减速系数。分别建立ngc、T45c、Nec的加减速系数表用于动态建模。

4 动态模型

根据稳态模型，采用动态系数法和转子动力学方程对发动机地面慢车以上动态工作过程进行建模。

模型输入参数为供油量Wf、环境温度T1、环境压力P1、负载杆角度α；模型输出参数为ng、T45、np。

（1）ng建模

给定燃气发生器初始转速ng（0）和供油规律，按照式（4）、（5）求出ΔWfc，根据（式11）插值求出Kng，则由式（6）得

（2）T45建模

利用式（9）求出ngc对应的稳态T45cs，然后根据式（12）求出KT45，则由式（7）得

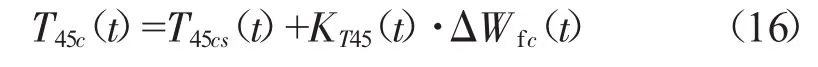
另外，由于温度传感器的延迟性，使得T45的测量值与实际燃气发生器出口温度存在一定的误差。因此，可加入惯性环节，使模型得到的T45值与测量值趋于一致。

（3）np建模

为了保证涡轴发动机在各种飞行条件下达到预定的功率并保持较高的效率，通常要控制旋翼转速保持不变，由于旋翼与动力涡轮是机械连接的，因此涡轴发动机控制规律通常为保持np不变。

当负载杆角度α变化时，旋翼的需求功率Nv也发生变化，造成动力涡轮输出功Ne与Nv不匹配，从而导致旋翼转速(也即np)变化。为了保证np等于设计转速，必须同时改变Wf，使得Ne与Nv重新匹配。

Ne和Nv直接影响np的变化，根据转子动力学方程，有如下关系

式中：Jpt为动力涡轮转动惯量。

给定α、供油规律和动力涡轮初始转速np（0）。计算np的关键是求解出Ne和Nv。Nv是np和α的函数，可根据给定的负载特性进行计算

与T45的求解类似，Ne也利用动态系数法进行计算。先根据式(10)得到Necs，然后根据式(13)求出KNe

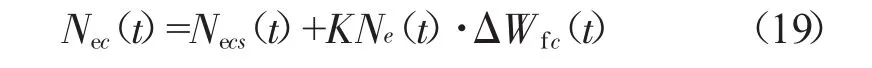
按照相似原理求出Ne，按照式(17)求出n˙p，则由式（8）得

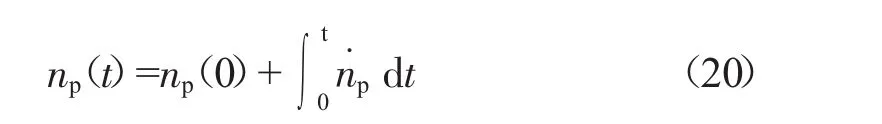
5 仿真结果

随机选取1组涡轴发动机地面试车数据，对简化模型的精度进行验证。所选试车数据对应的环境温度为27.5℃，环境压力为102.4 kPa。模型输出仿真结果如图3～6所示。

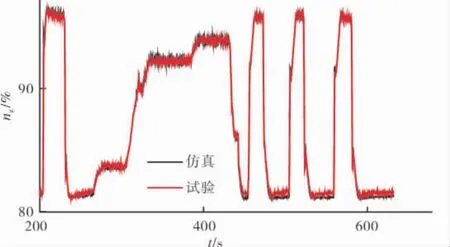
图3 燃气发生器转速ng仿真曲线

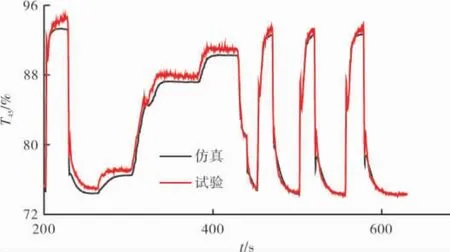
图4 燃气涡轮出口温度T45仿真曲线

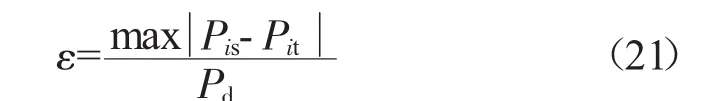
式中：Pis、Pit、Pd分别为各参数第i个仿真值、第i个实际测量值和设计值。得到各参数仿真误差，见表1。

ng仿真曲线如图3所示。从图3中可见，ng的仿真精度较高，从表1中可知，模型的稳态误差小于0.5%，动态误差小于3%。

T45仿真曲线如图4所示。从图4中可见，T45的仿真精度比ng的略差，从表1中可知，模型的稳态误差小于1.5%，动态误差小于4.5%。造成T45仿真误差稍大的主要原因是：T45的建模依赖于ng，误差的累积造成稳态时T45的仿真精度比ng的差。

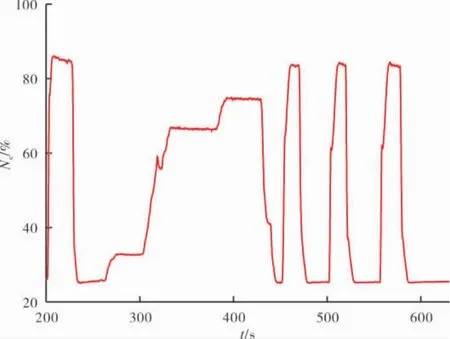
图5 动力涡轮输出功率Ne仿真曲线

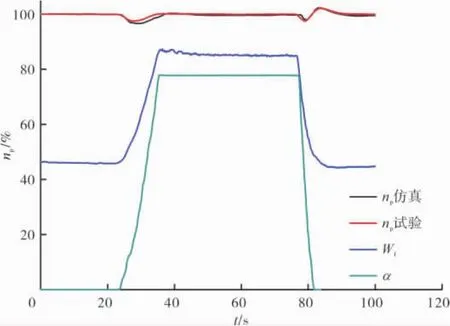
图6 动力涡轮转速np仿真曲线

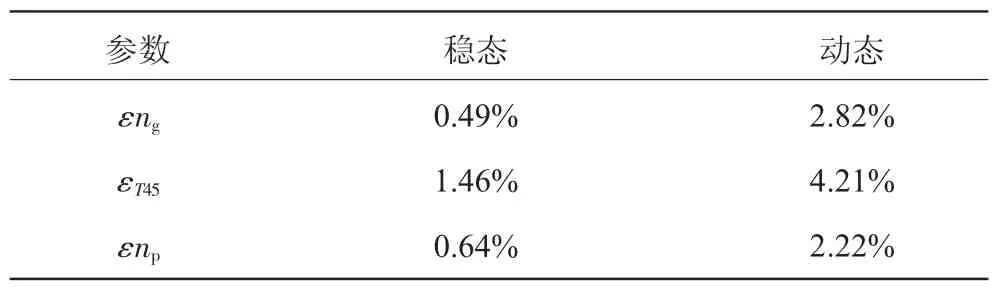
表1 模型仿真误差

另外，从图3、4中明显可见，当燃气发生器经过加速或减速到达稳态时，ng基本保持不变，T45测量值则缓慢变化。在建模时，将温度传感器近似作为1个惯性环节，在动态过程中T45仿真误差与惯性环节的参数选择有关，有待进一步对传感器模型进行修正，以减小T45仿真误差。

Ne仿真曲线如图5所示。Ne是用来计算np的，由于缺乏Ne动态数据，只能给出Ne的仿真值而无法验证其精度。

np仿真曲线如图6所示。对1个完整的加减载过程进行仿真。从图6中可见，模型可以较好地实现对的跟踪，从表1中可知稳态误差小于0.8%，加减载过程误差小于2.5%。

6 结束语

本文利用试车数据，采用插值法和动态系数法建立了涡轴发动机慢车状态以上简化模型。模型算法简单，计算量小，可满足实时性要求，不需要提供发动机特性图，符合机载计算能力要求，为传感器解析余度提供了1种简化数学模型。仿真验证表明：该简化模型具有较高的稳态和动态精度。

[1]鲁峰，黄金泉，陈煜，等.基于SPSO-SVR的融合航空发动机传感器故障诊断研究[J].航空动力学报，2009，24（8）：1856-1865.

[2]陈毅，黄金泉，张鹏.航空发动机控制系统传感器FDIA系统仿真[J].航空动力学报，2008，23（2）：396-400.

[3]蔡开龙，谢寿生，杨伟，等.基于改进LS-SVM的航空发动机传感器故障诊断与自适应重构控制[J].航空动力学报，2008，23（6）：1118-1126.

[4]侯胜利，李应红，李名魁，等.基于人工免疫网络模型的航空发动机传感器故障诊断[J].推进技术，2007（1）：86-91.

[5]Kim J H,Song T W,Kim T S,et al.Model development and simulation of transient behavior of heavy duty gas turbine[J]. Journal of Engineering for Gas Turbine and Power,2001,12（3）：589-594.

[6]Reed J A,Afjed A A.Computational simulation of gas turbine：part I-foundation of component-based models[J].Journal of Engineering for Gas Turbine and Power,2000,12（2）：366-376.

[7]Reed J A,Afjed A A.Computational simulation of gas turbine：partII-extensibledomainframework[J].Journalof Engineering for Gas Turbine and Power,2000,12（2）：377-386.

[8]周文祥，黄金泉，黄开明.航空发动机简化实时模型仿真研究[J].南京航空航天大学学报，2005，37（2）：251-255.

[9]冯海峰.航空涡轴发动机数学建模方法与控制规律研究[D].西安：西北工业大学，2007.

Research on Simplified Real-time Model of Turboshaft Engine

XING Yao-dong1，HUANG Jin-quan1，LU Feng1,YAO Wen-rong2（1.College of Energy and Power Engineering,
Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China 2.AVIC Aviation Motor Control System Institute,Wuxi Jiangsu 214063,China）

The simplified above-idle mathematic model of turboshaft engine was developed based on steady and transient engine ground test data because buliding an accurate on-board mathematics model for sensor fault diagnostics of aeroengine digital control system was quite difficult due to lack of detailed component characteristics.The interpolated algorithm,a transient coefficient method and rotor dynamics formula were used for the modeling,which makes the model support real-time simulation.Both steady operation and transient operation of the engine are simulated.The results show that the model has a satisfying precision,and can meet the demands of sensor fault diagnostics of aeroengine digital control system.

turboshaft engine；simplified modle interpolated algorithm;transient coefficient method；rotor dynamics

2011-11-25