Ar射频放电特性随时间演化的PIC/MCC模拟

张浚源 陈 峰 孙伟中 吕晓丹 贺平逆 苟富均,3

1（四川大学原子核科学技术研究所，辐射物理及技术教育部重点实验室 成都 610064）

2（贵州大学PSI研究所MEMS课题组 贵阳 550025）3（荷兰皇家科学院等离子体所 荷兰 2300）

射频溅射制膜装置中产生的非平衡态等离子体中的电子平均速度远大于离子，到达射频极板表面的电子数远多于离子。这些电子一部分与表面发生复合，大部分则聚集在极板表面，导致极板附近相对于等离子体区呈负电势，此负电势阻挡电子向极板处运动，并吸引正离子，导致极板附近区域离子密度与电子密度分离而形成鞘层[1–4]。等离子体中的离子经鞘层电场加速后轰击靶材使其发生溅射，溅射出的中性靶原子或基团大部分以扩散的方式沉积在基片上，但有些在输运过程中与等离子体碰撞，形成离子而轰击基片。这表明射频溅射制膜工艺是个非常复杂的过程，它包括等离子体放电行为、溅射产物的输运以及等离子体与基片表面相互作用[5,6]。为理解薄膜制备过程中的各种微观机理行为，有必要研究射频溅射工艺中等离子体放电行为。然而，常用的等离子体诊断手段仅能探测等离子体区域和预鞘层区域[4]，用实验手段了解射频放电行为有一定的局限性。

计算机模拟方法可有助于了解等离子体放电过程中的动力学行为。邱清泉[7]等模拟了平面直流磁控溅射放电等离子体，发现随着气压的升高，鞘层厚度基本不变，鞘层电势降会增大。Lee J K[8,9]等用一维等离子体粒子模拟法(particle-in-cell/Monte Carlo collision, PIC/MCC), 研究了容性耦合等离子体(Capacitively Coupled Plasma, CCP)源中的氩气放电行为，发现Ar+离子能量分布中的高能峰明显随着射频频率增大。Nanbu等[10]发现，相对于磁场而言，气压对电场的影响较小。

本文用PIC/MCC法利用一维模型模拟CCP源氩气放电过程中等离子体动力学行为。主要考察射频极板处和腔体中心处粒子流量、电流以及鞘层厚度随时间的演化关系。从理论上探讨射频等离子体放电过程中的物理和化学机制。

1 PIC/MCC模拟方法

PIC/MCC通过求解牛顿运动方程追踪大量超粒子(106–109个电子或离子)在外加电场及自洽电场中的运动过程，同时应用蒙特卡洛碰撞模型得到超粒子碰撞之后的运动状态，得到模拟系统中每个超粒子在求解时间内的运动轨迹[11-12]。可用统计平均法求解等离子体密度、温度、电势、电场和粒子通量等放电特性。通过跟踪不同时刻等离子体特性参量的变化，可以实现分析等离子体特性随时间的演化过程。粒子模拟不需要电子和离子处于平衡态的假设，因此可以对鞘层区域进行精确求解。

1.1 模拟模型

本文选用Georgieva和Bogaerts等[13]的CCP源模型。模拟过程中假设只有电场，并无磁场，位置方向为一维，速度方向为三维。模拟中腔体长度zn=2.5 cm。zn=0为接射频电压极板，zn=2.5 cm为接地极板，腔体内工作气体为氩气，气体初始温度为300 K，气压为26.66 Pa，初始电子和离子温度分别为2 eV和0.043 eV。模拟过程中，射频源电压为f=V0sin(wt) (V0=100 V,w=2pf)，本次模拟中频率f选为 13.56 MHz，并将腔体一维长度方向划分为100个格点，选用的时间步长为3.7´10–11s(电子)和 9.25´10–10s(离子)。

1.2 模拟流程

图1 PIC-MCC模拟单个循环流程Fig.1 PIC-MCC computational cycle, one time-step.

1.2.1 模拟初始化

初始值设置包括空间位置初始化和速度初始化。模拟开始前，电子和Ar+离子随机均匀的分布在每个网格点上，带电粒子速度分布服从麦克斯韦分布。

1.2.3 电场和电势的计算

用粒子云分室法(CIC)[12]计算每个格点的电荷密度，其代入泊松方程，求得它们的电势和电场。

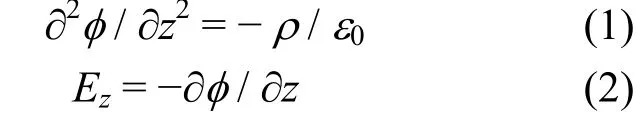
1.2.4 带电粒子受力

用CIC插值法求解每个带电粒子所处位置的电场大小。设带电粒子所处的位置为zpi，相邻两格点的位置和电场大小分别为zj,zj+1和Ej,Ej+1. 则zpi处的电场大小为：

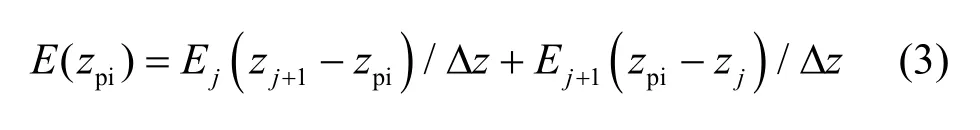
由F=Eq得到此处带电粒子所受的电场力为：

1.2.5 带电粒子在电场中的运动

带电粒子在电场力作用下运动，服从牛顿定律，因此，

用 leap_frog法[13]得到每个带电粒子的新位置和速度。

1.2.6 边界条件

模拟中所选模拟区域为射频极板与接地极板之间，边界为两极板(zn=0,zn=2.5 cm)。射频极板处(Zn=0)的电势随时间呈周期性变化f=Vsin(wt)，接地极板处(zn=2.5 cm)电势f= 0。

1.2.7 MCC模型

用MCC模拟粒子在运动过程中的碰撞过程，判定是否发生碰撞，发生何种碰撞。在一个时间步长Dt内，第i个粒子发生碰撞的概率为：

式中vi为带电粒子速度，sT为碰撞截面，Ei为带电粒子能量，ni为 Ar原子密度。求解Pi值即可判断粒子运动一段时间后是否会发生碰撞。取随机数R，若R>Pi，则不发生碰撞。若RPi，则发生碰撞。

1.3 碰撞反应

在Ar放电中，本文考虑以下5种反应[13-14]：

表1 模拟中碰撞反应的类型和阈值Table 1 All collisions considered in the model, with the corresponding thresholds for the cross-section data

2 结果与讨论

图2为射频极板处鞘层平均厚度与时间关系。由模拟初始条件可知，未加射频电压前，极板间粒子均匀分布且作无规则热运动。施加射频电压后，在极短时间内射频极板处形成厚0.28 cm的鞘层。初始阶段鞘层厚度随时间增加，经过2.65´10–4s趋于稳态，稳态鞘层平均厚度约为0.41 cm。

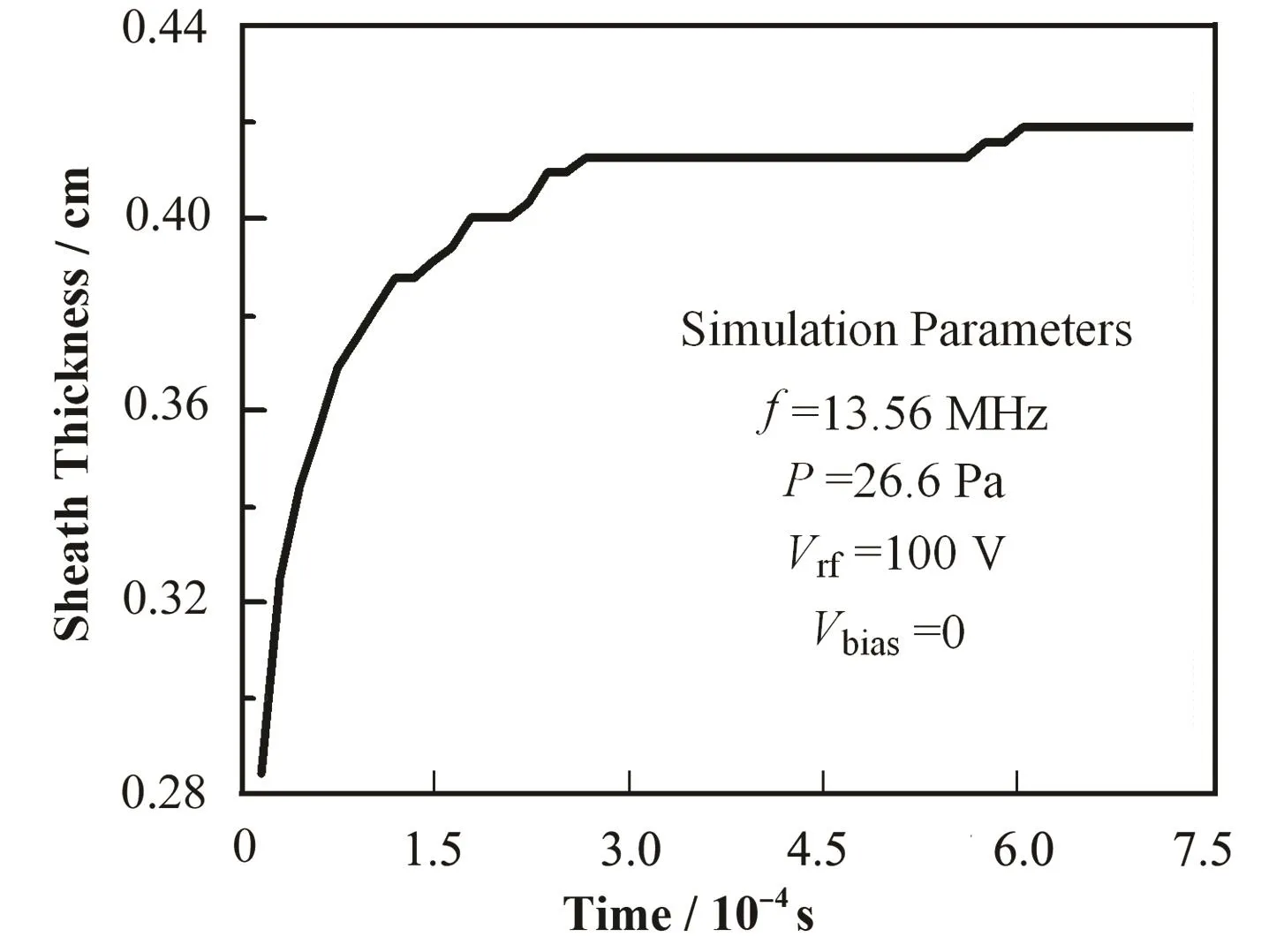
图2 射频极板处鞘层厚度随时间的变化关系Fig.2 Sheath thickness as a function of time at the powered electrode.

图3 (a)为电子和Ar+离子在射频极板处的平均粒子通量随模拟时间的变化，Ar+离子轰击射频极板上的粒子通量随时间增加而迅速减少。经2.65´10–4s后，极板处的Ar+离子和电子平均粒子通量趋于平衡。平衡后 Ar+离子的通量(6.8´1017m–2·s–1)大于电子的通量(6.4´1017m–2·s–1)。图 3(b)为电子和Ar+离子在腔体中心处的平均粒子通量随模拟时间的变化，腔体中心处的粒子通量随时间的增加迅速减少，1.03´10–4s后趋于平衡。4.12´10–4s后腔体中心处的电子平均通量与 Ar+离子平均通量几乎相等。比较图3(a)、(b)可知，极板处Ar+离子的平均粒子通量大于腔体中心处。

图3 电子和Ar+离子在射频极板上(a)和在腔体中心处(b)的粒子通量随模拟时间的变化关系Fig.3 Flux of electron and Ar+ as a function of time, at the powered electrode (a) and middle of the reactor (b).

图4 为射频极板处和腔体中心处平均电流密度随时间的变化。由图 4(a)，射频极板处的平均电流密度随时间的增大而减小，2.65´10-4s后平均电流密度趋于平衡。当射频极板处平均电流密度趋于稳定时，电子的平均电流密度几乎为零，而Ar+离子的平均电流密度为 3.0´10–3A/m2。图4(b)是腔体中心处的电子和 Ar+离子平均电流密度随时间的变化，在腔体中心处Ar+离子平均电流密度基本保持不变(7.0´10–6A/m2)，而电子平均电流密度随时间的增加逐渐减小，在1.03´10–4s之后趋于平衡，达到0.32 A/m2。从图中还可以看出，腔体中心处电子的总电流密度大于Ar+离子。

图4 射频极板处(a)和腔体中心处(b)电流密度随模拟时间的变化Fig.4 Current density as a function of time, at the powered electrode (a) and middle of the reactor (b).

图5 所示为一个放电周期内，电场强度在不同相位(i=0, p/2, p,3p/2)时的空间分布。在等离子体区域(0.75–1.75 cm)，电场强度很小且不随时间发生变化。在鞘层区域和预鞘层区域(分别为射频极板附近0.75–0 cm和接地板附近1.75–2.5 cm)，电场随时间发生变化。在i=0时，z=0 和z=2.5 cm处，电场分别为–14387 V/m，15433 V/m 。在i=p/2时,z=0和z=2.5 cm 处，电场分别为–26255 V/m，3512.5 V/m。在i=p时，z=0 和z=2.5 cm处，电场分别为–15190 V/m，14575 V/m。在i=3p/2时，z=0 和z=2.5 cm处，电场分别为–3296.2 V/m，26466 V/m。

图5 单个射频放电周期内电场在不同相位的空间分布Fig.5 Electric field at different phases of an RF cycle.

射频放电中极板间的电流由位移和传导电流组成。位移电流是由随时间变化的电场产生的，传导电流的主要载流子为电子[15]。鞘层内(0–0.5 cm 和2–2.5 cm)电子密度很低(图7a)[1,3,7]，而电场强度随时间变化(图5)，则此区域内电流密度主要由位移电流贡献，故Ar+离子的平均电流密度大于电子的平均电流密度(图 4a)。在等离子体区域(0.75–1.75 cm)，电场强度几乎不随时间发生变化(图5)，这意味着位移电流为零，则该区域的电流主要由传导电流贡献，故此处的Ar+离子平均电流密度小于电子的平均电流密度(图4b)。

在 e+Ar→2e+Ar+电离反应中，有大量 Ar+离子产生，同时模拟中也有大量Ar+离子轰击到极板上而损失掉。图6(a)、(b)和(c)分别为腔体内产生和损失的Ar+离子数密度以及腔体内总的Ar+离子数密度随时间的变化关系。由图可知，随模拟时间的增加，参加电离反应产生的Ar+离子数密度增多，而损失的Ar+离子数密度和腔体内的Ar+离子数密度减小。1.03´10–4s时，产生和损失的Ar+以及腔体内的离子数密度趋于稳定。

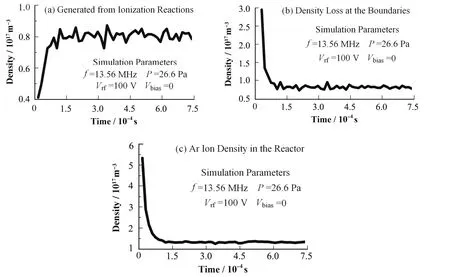
图6 离化反应产生的(a)、损失的(b)和腔体内的(c)Ar+离子数密度Fig.6 Ar+ ion densities generated from ionization reaction(a), lost at the boundaries(b), and in the plasma reactor(c).

图7给出了等离子体达到平衡后等离子体特性参量对时间平均后的空间分布。图 7(a)是等离子体达到平衡时电子和Ar+离子数密度的空间分布，在中心等离子体区(0.75–1.75 cm)和预鞘层区(0.5–0.75和 1.75–2.0 cm)，电子和离子密度相等，而鞘层区域(0–0.5 cm和2–2.5 cm)电子密度明显小于离子密度。图7(b)为等离子体达到平衡时由空间电荷形成的电势在空间的分布，鞘层区域相对中心等离子体区域呈负电势，中心等离子体区电势基本保持不变，而鞘层区域电势迅速下降。由式(1)，由于中心等离子体区净电荷密度r=0(图7a)，因此电势基本保持不变；而在鞘层区域r>0(图7a)，极板间净电荷为正电荷，因此电势迅速下降。图 7(c)为等离子体达到平衡时电场强度的空间分布，在腔体中心处电场强度几乎为零，而在鞘层区域电场强度变化显著。由式(2)，在中心等离子体区域电势无变化，因此电场强度很小且基本不变；而在鞘层区域，电势的迅速下降导致了电场强度的剧烈变化。图7(d)为平衡时电子和 Ar+离子能量的空间分布，Ar+离子的能量在等离子体区域仅0.04 eV左右。因此，在等离子体区域，粒子的热运动占优势。离子进入鞘层区域后受到鞘层电场的加速作用(图 7c)，其能量明显升高，最高可达4.58 eV(在两个极板处)。电子则在刚进入鞘层阶段能量有所增加，最高能量为3.41eV(0.25和2.25cm处)，当电子进入鞘层之后，由于鞘层的阻碍作用其能量迅速下降。

图7 Ar+离子和电子的平均密度(a)、电势(b)、电场强度(c)、平均能量(d)Fig.7 Density(a), potential(b), electric field(c) and averaged energy (d) of electron and Ar+ ion.

3 结论

本文通过 PIC-MCC方法利用一维模型模拟了CCP源氩气放电过程中等离子体的动力学行为，通过对模拟结果分析，得到以下结论：

1) 射频极板处鞘层在极短时间内形成，其厚度随着时间的增加而增厚，2.65´10–4s时鞘层厚度基本稳定，厚度为0.41 cm。

2) 射频极板处粒子通量随时间的增加而逐渐减小，之后射频极板处粒子通量达平衡，整个模拟中极板处离子通量略大于电子通量。腔体中心处的粒子通量也随时间的增加逐渐减少最后逐渐趋于平衡且电子平均通量几乎与Ar+离子平均通量相等。

3) 等离子体区域电流密度主要受传导电流影响，其电子平均电流密度大于Ar+离子平均电流密度；鞘层区域主要受位移电流影响，其电子平均电流密度小于Ar+离子平均电流密度。

1 赵化侨. 等离子体化学与工艺[M].合肥: 中国科学技术大学出版社. 1993.ZHAO huaqiao. Plasm chemistry and technology[M].Hefei: University of Science and Technology of China Press. 1993

2 王德真, 张建红, 宫野. 气体放电阴极鞘层氩离子的自洽蒙特卡洛模拟[J]. 计算物理. 1995, 12(4): 483–488 WANG Dezhen, ZHANG Jianhong, Miyano. A self-consistent monte carlo simulation of ions in cathode sheath of argon gas discharges[J]. Computatinal physics,1995, 12(4):483–488

3 WANG Shuai, XU Xiang, WANG Younian. Frequency matching effects on characteristics of bulk plasmas and sheaths for dual-frequency capacitively coupled argon discharges: one-dimensional fluid simulation[J]. Plasma Sci.Technol, 2008, 10: 57–60

4 WANG Shuai, XU Xiang, WANG Younian. Numerical investigation of ion energy distribution and ion angle distribution in a dual-frequency capacitively coupled plasma with a hybrid model[J]. Physics of Plasmas, 2007,14: 113501

5 严心一. 薄膜技术[M] .北京: 兵器工业出版社, 1994 YAN Xinyi. Thin film technology[M]. Beijing: Weapons industry press, 1994

6 杨邦昌, 薄膜物理与技术[M]. 成都: 电子科技大学出版社. 1994 YANG Bangchang. Thin film physics and technology[M].Chengdu: University of Electronic Science and Technology of China Press. 1994

7 邱清泉, 励庆孚. 工作参数对平面直流磁控溅射放电特性的影响[J]. 核聚变与等离子体物理. 2009, 29(2):182–187 QIU qingquan, LI qingfu. Influence of operating parameters on discharge characteristics of planar DC magnetron[J]. Unclear fusion and plasm physics, 2009.29(2): 182–187

8 Lee J K, Manuilenko O V, Babaeva N Y,et al. Ion energy distribution control in single and dual frequency capacitive plasma sources [J]. Plasma Sources Science &Technology, 2005. 14(1): 89–97

9 Lee J K, Babaeva N Y, Kim H C,et al. Simulation of capacitively coupled single- and dual-frequency RF discharges[J]. Ieee Transactions on Plasma Science, 2004,32(1): 47–53

10 Nanbu K, Kondo S. Jpn J. Analysis of three-dimensional dc magnetron discharge by the partial-in-cell/Monte Carlo method[J].App1.Phys.Part l, 1997, 36(7B): 4808–4813

11 Tao W F, Cai D S, Lembege B. et.al. Computer Physics Communications[J],2008. 179(12): 855-864.

12 Birdsall C K, Langdon A B. Plasma Physics via Computer Simulation[M].McGraw- Hill, New York, 1985

13 Georgieva V, Bogaerts A, Gijbels R. Numerical study of Ar/CF/N discharges in single-and dual-frequency capacitively coupled plasma reactors[J]. Journal of Applied Physics, 2003, 93(5): 2369–2379

14 杨津基. 气体放电[M]. 北京:科学出版社, 1983 YANG jinji. Gas discharge[M]. Beijing: Science Press,1983

15 Liebermanallan M A, Lichtenberg J. Principles of plasma discharges and materials processing[M]. New Jersey,2005