基于STAR模型的我国PPI指数描述性统计研究
2012-06-30张宏平张岳峰
○张宏平 张岳峰
(西安财经学院 陕西 西安 710100)
一、引言
工业品出厂价格指数是反映全部工业产品出厂价格总水平的变动趋势和程度的相对数。通过工业生产价格指数能观察出厂价格变动对工业总产值的影响。本文主要研究我国PPI变动的总体趋势,以期加深对该经济指标的理解,并对今后的经济政策的制定提供相关信息。在以往的研究中我们发现许多的宏观经济变量都在一定程度上表现出非线性的特性,比如汇率、失业率、股指等等。目前,关于非线性模型的研究很多,本文试图利用STAR模型来描述我国的PPI数据,因为PPI属于周期性指标,它会随着经济的周期性波动而发生变化,STAR模型可以实现两个机制之间的平滑转移而非突然地跳跃,这可以很好地描述因突发性的经济现象给经济带来的负面影响。国内外基于STAR模型的实证分析也很多。例如:Sarantis(1999)使用STAR模型研究1980年至1990年十大主要工业国家的月度实际汇率。实证结果显示,除了荷兰与瑞士以外,其他国家的实际汇率序列均有明显的非线性关系,他还根据数据特征选择不同的非线性模型(ESTAR和LSTAR)来拟合数据,并且发现其中三国实际汇率序列使用LSTAR模型拟合较为适合,而其他五国则应将模型设定为ESTAR。估计得到的模型都通过了诊断检验,能够对实际汇率提供合理的解释。David G.(2003)分别基于线性模型、LSTAR模型和ESTAR模型,使用1975年1月至1995年4月的季度数据,研究英国股指与宏观经济变量(失业率、工业生产指数、消费物价指数、广义货币供给余额)之间的相关性,并使用1996年1月至2001年4月的数据作为样本外预测。实证结果表明,ESTAR模型的样本内与样本外的预测效果均优于LSTAR模型和线性模型。Jiazhou所做的关于瑞士的工业价格指数的研究,用STAR很好地刻画了该国的工业价格指数变化。我国学者刘柏、赵振全基于STAR模型的中国实际汇率非线性态势预测表明了汇率向购买力平价转移的趋势。谢赤、戴克维、刘潭秋应用平滑过渡自回归(STAR)模型来揭示人民币实际汇率的动态行为,研究发现,以logistic函数作为过渡函数的STAR模型能很好地描述人民币实际汇率的行为。
二、平滑移动自回归模型(STAR)
平滑移动自回归模型是由Tera¨svirta及Anderson在1992年所发展的,最初是被用在研究景气循环方面的,其模型表达式如下:

其中,yt表示被解释变量,它可以是具体的经济成果。xt表示解释变量组成的向量,包括目标变量yt的直到k阶的滞后变量,即有:xt=(1,yt-1,……,yt-k)'。β=(β0,β1,…βk)',θ=(θ0,θ1,…θk)'为参数变量。F(yt-d)是一个连续的过渡函数,也称转换函数,取值范围[0,1],通常具有如下形式:

其中,γ为过度参数,γ>0决定了两个制度之间过渡的平滑性和过渡速度大小,yt-d是延迟变量,d是延迟阶数。
转换函数为(3)式的STAR模型称为LSTAR:当γ→∞时,如果 yt-d≤c 则 F(yt-d)=0;如果 yt-d>c 则 F(yt-d)=1。当 γ→0,F(yt-d)就会变成一个 AR(p)模型。
转换函数为(4)式的STAR模型称为ESTAR:ESTAR的转换函数关于yt-d=c是对称的,当γ→∞或γ→0时,转换函数就会退化为常数(1或0)使得ESTAR模型退化为线性模型。两种转换函数都将随着γ的增大而变得陡峭,也就意味着转换速度变得越来越快。
三、模型的构建与转换函数的选择
基于以上讨论STAR模型的构建可以按照下面的步骤来进行。
第一,根据所研究课题定义一个恰当的k阶线性自回归模型 AR(k)。
第二,针对不同的d值做非线性检验,选择最合适的延迟阶数。
非线性检验的核心思想是Luukkonen、Saikkonen和Tera¨svirta(1988)提出的,即将转换函数 G(st,γ,C)用适当的泰勒级数展开式近似值替代,这样就避免了不能直接对线性与非线性假设进行检验的问题,并且在线性原假设成立的条件下,LM统计量渐进服从x2分布。我们将转换函数在γ=0处按三阶泰勒公式展开得到如下的辅助回归方程:
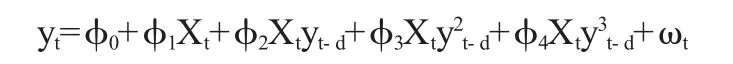
其中,Xt=(yt-1,yt-2,…,yt-k)',ωt是误差项。
其线性测试为H0:φ2=φ3=φ4=0。对上式进行F检验,求出所对应的F值。如果有多个d值所对应的上式的原假设被拒绝,就选具有最大F值或对应最小的k值作为选取d值的依据。
第三,模型选择。在线性假设被拒绝的情况下,在LSTAR模型与ESTAR模型之间做出选择。该步可由以下的一系列嵌入测试完成:

如果拒绝H4,应选择LSTAR模型;如果接受H4而拒绝H3,则应选择ESTAR 模型;如果接受H4和H3而拒绝H2,应选择LSTAR模型。通过F检验,选择具有最大F值所对应STAR模型。
四、实证分析
1、数据
本文以我国的工业品出厂价格指数为研究对象,数据来源于凤凰卫视数据库。为了研究2007年爆发的全球性金融危机对中国经济的影响,收集的数据为2000年1月到2010年12月的月度工业品出厂价格指数。用I(t)表示从每一个时点t观察到的PPI指数,并对该指数做季节处理和一阶差分,记为:
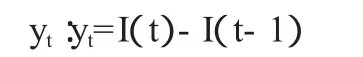
其基本趋势如图1。
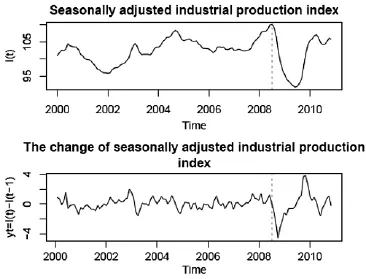
图1 PPI数据趋势图
从图1中我们可以清楚地看到我国的PPI指数从2000年初到2008年上半年波动趋势比较缓和,然后突然急转直下达到了一个历史低点。如果所考察数据是非线性的,那么使用线性模型做估计和预测就会导致错误,因此我们有必要进行一个线性测试。在进行线性测试之前,让我们先做一个诊断看该时间序列数据是否存在断点,为了测试结构上的变化和断点,我们通常用邹检验来考察,观察整体回归是不是比较断点分开的两个自回归更加有效。
首先我们记整个时间序列数据构成的模型是一个p阶的自回归模型yt。
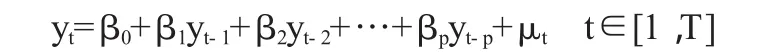
如果我们把数据在点T0处分成两组,被认为是一个潜在的断点,那么我们就会得到如下的两个自回归模型:

检验的原假设:β10=β20,β11=β21,…,β1p=β2p;被择假设:至少有一个等式不成立。
检验统计量:
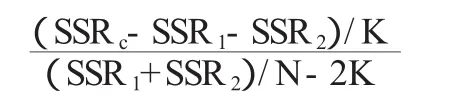
其中K是总的参数的个数,SSRc为总的残差平方和,SSR1和SSR2分别为两个分模型的残差平方和。该检验统计量近似服从自由度为(K,N-2K)的F分布。
2、断点检验
对于整个数据集而言,根据AIC统计量的定义,需要选择AIC统计量最小的那组自回归模型,从表1中可以看出,四阶AR模型的AIC统计量最小,因此将PPI序列的线性自回归模型设定为AR(4)模型,确定滞后参数k为4最为适宜。而且残差序列不存在自相关,AR(4)的模型估计结果如下:

表1 自回归阶数选择

接下来对所有的时间点进行邹检验。在原假设成立的条件下邹检验和F检验的结果如图2所示。

图2 断点检验
为了求得潜在断点的个数我们对每个子模型所有可能的断点都进行了检验并计算了它们的BIC值和RSS值。结果如表2:检验结果表明在2008年7月数据出现了一个明显的断点,因为该点对应的BIC值最小并且RSS值也相对较小。据此我们将数据集从该点断开成两个部分分别进行拟合,拟合结果见图3。
图3给出了三条曲线,一条是用原始数据拟合的曲线,另外两条是依断点断开的两条拟合曲线,通过比较这两种线性模型的结果我们发现分阶段模型明显优于未分阶段模型。但是这种拟合效果并非最好,数据中很可能包含了非线性元素,接下来我们希望用一个非线性的模型来描述这一过程。
3、非线性检验和估计
我们已经根据AIC信息准则确定了AR(4)的线性部分,接下来要做的是非线性分析。首先是延迟阶数的选择,线性测试结果见表3,从表3中可以看出,在d为1和2时均在5%的显著水平上拒绝序列为线性的虚拟假设,而d为2时的F统计量比为1时的要大,因此选择d为2作为模型的延迟阶数。
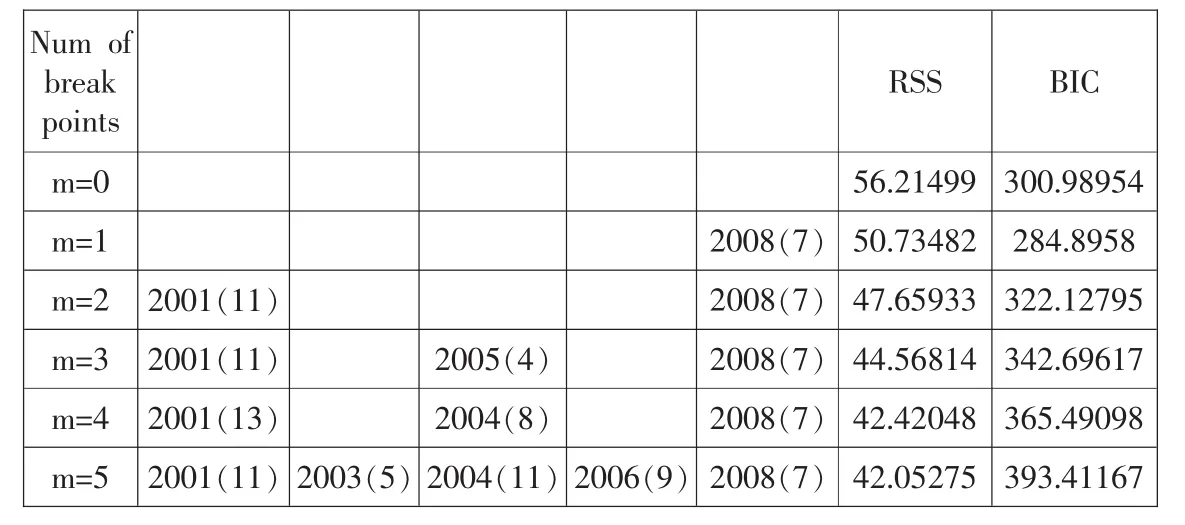
表2 BIC值和RSS值

图3 分段拟合图

表3 延迟阶数选择

表4 STAR模型的选择
表4中的三个检验结果若拒绝H4则表示选择LSTAR模型,若接受H4拒绝H3则表示选择ESTAR模型,如果接受H4和H3而拒绝H2,则应选择LSTAR模型。由表4的结果可以看出PPI序列适合ESTAR模型。
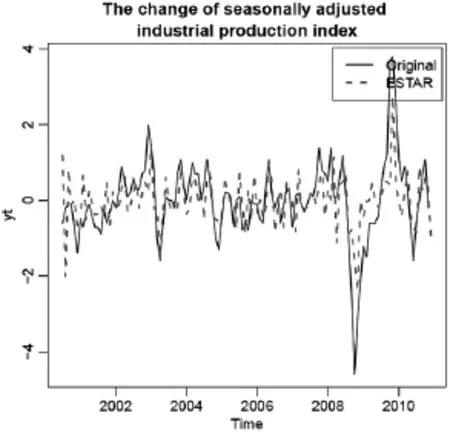
图4 PPI数据ESTAR模型拟合图
参数k、d及转换方程式确定后,模型的形式也就确定了,由于STAR模型为非线性模型,所以其模型估计一般不采用普通最小二乘法(OLS),本文采用非线性最小二乘法(NLS)对参数进行估计。估计结果如下:

模型中常数项被忽略了,因为他们在模型中并不重要,模型的拟合图形如图4所示。
通过对ESTAR模型拟合图和原始数据图的比较我们发现模型在2008年7月的点上不能很好的模拟数据,这属于异常值,因为这段时间工业品出厂价格指数受到国际金融危机的冲击。估计的阈值C=-2.1560,处在yt的观察值范围之内,但是仍然比较低。
五、结语
在本文中,我们研究了中国2000年1月至2010年12月的工业品出厂价格指数,首先我们对数据进行了结构性分析和非线性检验,当线性检验被拒绝之后我们就试图寻找一种非线性的模型来对数据进行描述,由于平滑转移自回归模型它具有在两个机制之间平滑过渡的良好特性故我们考虑用它来对数据进行分析,其次STAR模型具有ESTAR和LSTAR两种转换函数,分析之前我们需要选择适合的转换函数,这可以通过一系列的嵌入式测试来完成,经过测试我们选择ESTAR模型对数据进行了拟合,最后从估计结果我们得到以下结论:第一,大多数的观察值位于指数函数的右尾,模型在一定程度上表现出了 LSTAR 行为的特征。第二,γ 的估计值γ^=4.8/σ^=2.34 表明两个机制之间的转换也是相当缓慢的,说明我国的工业品出厂价格指数基本上保持了平稳缓和的态势,除了个别时段会有反常出现大幅波动,例如2008年全球金融危机的影响。第三,从模型估计的标准差我们得到有20%的可能性从线性模型过渡到非线性模型,因此我们可以认为ESTAR模型能够比线性自回归模型更好地刻画我国的工业品出厂价格指数。
[1]Sarantis,N:Modeling non-linearities in real effective exchange rates[J].Journal of International Money and Finance,1999(18).
[2]McMillan,David G.:Non-linear Predictability of UK Stock Market Returns[J].Oxford Bulletin of Economics and Statistic,2003(65).
[3]Jia Zhou:Smooth Transition Autoregressive Modles A Study of The Industrial Production Index of Sweden[J].Statistics June,2010.
[4]刘柏、赵振全:基于STAR模型的中国实际汇率非线性态势预测[J].数量经济技术经济研究,2008(6).
[5]谢赤、戴克维、刘潭秋:基于STAR模型的人民币实际汇率行为的描述[J].金融研究,2005(5).
[6]Tera¨svirta,T.:Specification,estimation,and evaluation of smooth transition autoregressive models[J].Journal of the American Statistical Association,1994(89).
