考虑资金时间价值的水运工程索赔谈判

查京民，董冰冰

（天津大学管理与经济学院，天津 300072）

0 引言

水运建设工程尤其是国际承包工程项目产生的施工索赔谈判问题中，在双方达成协议较为困难的情况下，应如何适时做出合理的对策，即是否退让以及退让的程度以使谈判达到双方可接受的结果，是谈判双方需要认真研究的问题。前人在应用博弈论解决施工索赔问题方面已有研究，李艳梅应用完全信息动态博弈中鲁宾斯坦（Rubinstein，1982）提出的局中人轮流出价讨价还价模型研究了BOT项目特许期的问题[1]；Ren Z.，Anumba C.J.强调了学习对于多代理机制的重要性，并且提出了具体的贝叶斯（Bayesian）学习模式来解决多代理的施工索赔谈判问题，这样有利于提高谈判能力和收敛速度[2]；随后，他们又提出了把Zeuthen的讨价还价模型和贝叶斯（Bayesian）学习机制结合起来用以解决施工索赔谈判问题，体现了建设工程索赔的特点[3]。

由于水运国际承包工程项目的资金量较大，如何考虑时间价值因素是有待解决的重点之一。袁宏川，李慧民认为施工索赔谈判是一种较为典型的博弈形式，他们首先用轮流出价的博弈模型来描述业主、承包商之间讨价还价的过程，然后估计对方的保留值并且用贝叶斯理论调整此保留值，以此确定报价策略，最后提出考虑资金时间价值的情况[4]。吕文学，聂建明用动态博弈模型研究了变更定价问题，通过求解博弈树得出了承包商的最优报价公式[5]；随后他们又把资金时间价值作为一种沉默成本考虑，用动态博弈模型和鲁宾斯坦（Rubinstein，1982）讨价还价理论得出双方在各阶段的最佳报价[6]。

综上所述，应用博弈论解决施工索赔问题，大致分为两个分支，一是应用决策树得出最优索赔报价，已有文章将资金时间价值作为影响索赔报价的变量之一考虑；另一方面是应用贝叶斯（Bayesian）理论修正对对手保留值的估计，结合Zeuthen谈判策略得出最优报价，现有文章提及到资金时间价值，但并没有把资金的时间价值作为变量融入模型当中。

本文针对水运工程资金量大的特点，考虑了资金时间价值，并且将其融入索赔博弈模型当中，应用Zeuthen谈判理论及贝叶斯理论得出了水运工程施工索赔谈判中的退让方以及退让方的最佳报价。

1 水运工程施工索赔谈判理论分析

水运工程施工索赔过程是一个两人讨价还价博弈的过程，故可以用两人讨价还价博弈理论分析，由于业主和承包商需要长期合作，不是完全的对立关系，这里用合作博弈的理论进行分析。两人讨价还价会有一个谈判破裂点，任何谈判都有破裂的可能，在谈判破裂的情况下博弈方也可能得到利益[7]。例如承包商向业主索赔500万元并且不做出退让，业主认为索赔额过高，并且估计在仲裁或者诉讼的情况下索赔额在450万元左右，这时谈判就会破裂。两人讨价还价博弈的另一个特点是每个博弈方的得益和效用的对应情况是不同的，例如500万元对于业主是储备资金，但对于承包商是急需的周转资金，所以同样的500万元对于承包商的效用显然更大，这种特点我们也可以用博弈一方占用资金产生的时间价值表示。

资金的时间价值，即折现因素，它反映了财务计算中一定数额的资金在不同的时间点上价值量的差额。它产生的原因是由于资金在投资过程中随着时间的推移产生收益，资金的时间价值反应了资金的使用成本，不同的谈判方对于资金的使用成本是不同的。

施工索赔过程归根到底是一种谈判过程，根据Zeuthen的单向让步谈判理论，谈判双方中风险承受能力小的一方，会在下一轮报价中做出退让，退让的程度是使对方和己方的风险承受能力相等或小于己方的风险承受能力[8]。在施工索赔博弈模型中，我们考虑承包商和业主的最大风险承受能力Pcmax、Pemax，当本轮报价中Pcmax＞Pemax时，下一轮报价中业主会做出让步，使得Pcmax≤Pemax，这样每轮出价过程中，双方的最大风险承受能力都会减小，直至最大风险承受能力减小到趋于零，并且此时的索赔额不低于谈判破裂点的索赔额，双方达成一致，得到最终索赔额。

2 水运工程施工索赔谈判模型的建立

考虑资金时间价值的水运工程施工索赔谈判博弈模型可以从业主或者承包商的角度去建立，本节首先站在承包商的角度，建立索赔谈判博弈模型，最后相应地给出站在业主角度建立索赔谈判博弈模型的方法。

承包商首先估计出己方实际损失Rr以及谈判破裂点d，然后根据Rr及经验估计业主保留值R；根据业主的第一次报价及己方经验对业主保留值进行修正得到修正后的业主保留值R′；根据谈判双方第一次报价及Rr和R′得到双方的效用公式；将资金时间价值作为变量体现在效用公式中，对效用公式进行修正；根据Zeuthen的单向让步谈判策略及效用公式对双方的最大风险承受能力进行求解；比较双方最大风险承受能力的大小，确定让步方及让步程度。

2.1 对业主保留值的估计

承包商首先要计算出己方实际损失Rr、谈判破裂点的索赔额d，最终的索赔额不低于d索赔才能达成一致，否则索赔结束进行仲裁或诉讼，然后根据实际损失及经验预测业主的保留值及其概率分布，见表1。

表1 承包商对业主保留值及其概率的先验预测

在业主出价前，承包商对业主保留值的估计为：

2.2 对业主保留值的修正

根据贝叶斯定理公式和全概率公式：

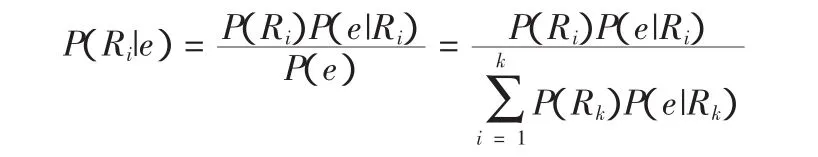
式中：e为业主的报价；R为业主的保留值；P（Ri|e）为业主报价为e时，保留值为Ri的概率；P（Ri）为业主的保留值为Ri的概率；P（e|Ri）为业主的保留值为Ri时，报价为e的概率；P（e|Rk）为业主的保留值为Rk时，报价为e的概率；P（Rk）为业主的保留值为Rk的概率。

承包商可以根据业主第一次报价和自己的经验对业主的保留值的概率进行修正，P（Ri|e）可以由表2求出。

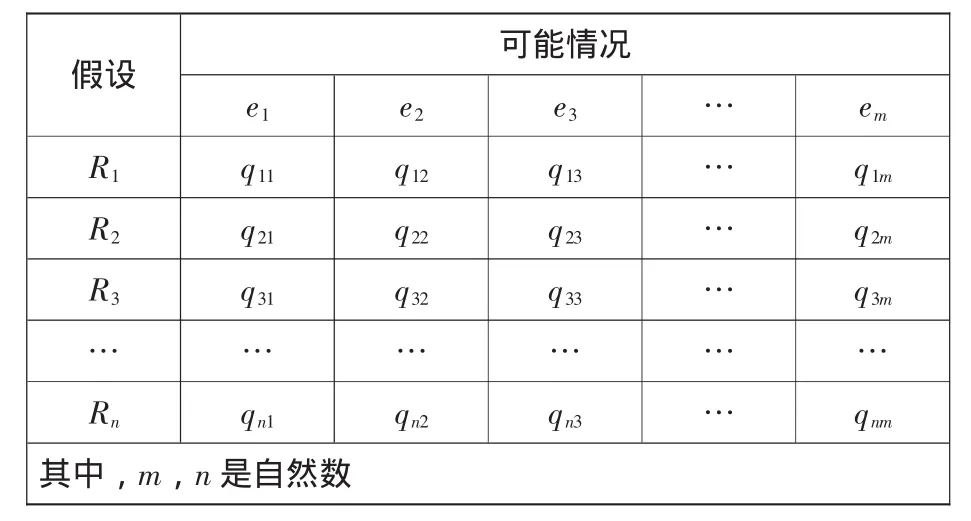
表2 对业主保留值概率的修正

进行概率修正后，承包商对业主保留值的估计为：

2.3 效用的求解

这里假设效用函数是线性的，则业主的效用函数为：

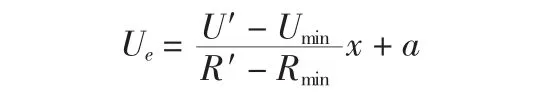
式中：Rmin为业主报价的最小值，这里认为是业主第一轮报价值，并且认为此时业主的效用Umin为1；R′是承包商根据业主报价，对其保留值的修正，并且认为此时业主的效用U′为0.6，即（Rmin，1），（R′，0.6）这两点可以确定业主的效用函数。

同理，承包商的效用函数为：

式中，Rcmax为承包商的最高报价，这里认为是承包商的第一次报价，并且认为此时承包商的效用Ucmax为1；Rr为承包商的实际损失，并且认为索赔额为实际损失值时，承包商的效用Ur为0.6。

2.4 效用的修正

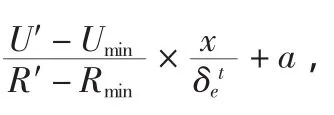
施工索赔谈判期越长，业主、承包商付出的资金时间价值就越多，并且每次谈判都会产生人员、场地等费用，所以考虑资金时间价值后，理性的谈判方都会积极谈判，合理让步，使施工索赔谈判过程缩短以提高施工索赔效率，减少施工索赔成本，对业主、承包商双方都更为有利。

2.5 最大风险承受能力的求解

式中：Ucct为在第t轮报价中业主接受承包商报价，承包商得到的效用；Ucet为在第t轮报价中承包商接受业主报价，承包商得到的效用。

业主的最大风险承受能力为：

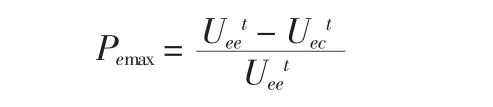
式中：Ueet为在第t轮报价中承包商接受业主报价，业主得到的效用；Uect为在第t轮报价中业主接受承包商报价，业主得到的效用。

2.6 谈判双方在t+1轮报价中的策略

用上述方法求得承包商和业主的最大风险承受能力后，比较二者的大小，如前所述，最大风险承受能力较小的一方在t+1轮报价中会做出退让，退让的幅度为使对方的最大风险承受能力小于等于己方的最大风险承受能力。这样双方在施工索赔过程中，最大风险承受能力会越来越小，直到最后趋于零，并且最终索赔额高于谈判破裂点索赔额时，双方达成一致，索赔结束。

2.7 站在业主角度的索赔谈判模型

相应地，业主方首先根据索赔情况估计出承包商的实际损失，计算出己方的保留值，根据承包商实际损失及经验估计承包商报价的概率分布，根据承包商的第一次报价对承包商实际损失进行修正，然后得到考虑资金时间价值的效用函数，进而求得双方的最大风险承受能力及退让情况。

3 案例分析

3.1 案例背景

某国际水运工程施工合同承包的内容有航道清淤与码头修建，在清除航道淤泥的过程中，遇到飓风天气，清淤工作暂停产生了工期的延误和费用的增加，由于业主要求按时完工，承包商增加机械与人工的投入。为此，承包商向业主提出费用索赔。

3.2 谈判准备阶段

3.2.1 承包商实际损失估算

5.2 基因探针 真菌核糖体RNA的碱基序列由可变区和保守区组成;利用保守区可设计通用探针；利用可变区可设计针对不同菌种的特异性探针。吗啉寡聚物(morpholino oligomers，MORFs)通过Watson-Crick碱基配对与其互补的DNA或RNA结合，并对核酸酶具有抵抗性，与血清蛋白质结合率低，可进入细胞并在循环中被迅速清除。因此，有研究[55]用99mTc标记的MORFs探针靶向真菌核糖体RNA，结合SPECT成像用于检测曲霉菌感染，这有望成为诊断曲霉菌感染的新方法。

承包商的实际损失为Rr=5696908元≈570万元，考虑到与业主方的后续合作项目需要良好的合作关系以及仲裁诉讼成本，谈判破裂点的索赔额为500万元，在整个索赔谈判过程中，当业主的索赔额低于500万元且无还价余地，索赔结束，承包商要求仲裁或诉讼。承包商根据以往经验，将谈判空间设定为 [-10%，15%]，则最乐观报价定为570×（1+15%）=655.5万元，以10万元计，则承包商的实际损失为570万元，最乐观报价为660万元。

3.2.2 对业主保留值的估计

承包商根据自己的经验，对业主保留值及概率进行估计，见表3。

表3 本案例承包商对业主保留值及其概率的先验预测

同时，承包商对业主的报价策略做出评估，进而对先验分析中的业主保留值概率进行修正，见表4。

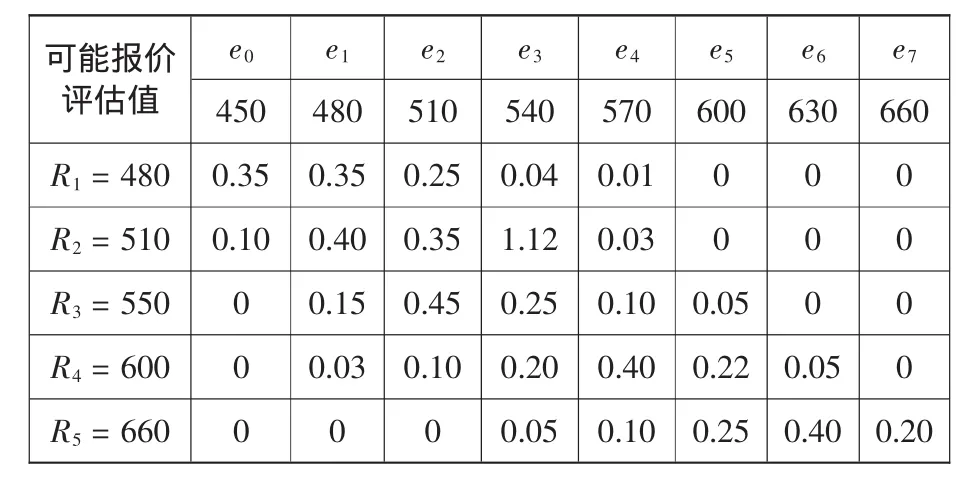
表4 对业主保留值概率的修正

3.2.3 消耗系数δ的确定

选取项目实施期间人民币存款一年期的利率ri=3.5%，假设讨价还价一回合所用的时间为1周，则δe=1/（1+ri/52）=0.99933，承包商的企业利润率为5%，则δc=1/（1+rc/52）=0.99904。

3.3 谈判的讨价还价阶段

3.3.1 讨价还价第一回合

这一回合，承包商报价660万元，业主还价480万元，即承包商的最乐观报价为660万元，业主的最乐观报价为480万元。

3.3.2 对业主保留值的修正

根据业主的第一回合报价，承包商对业主的保留值及其概率进行了修正：

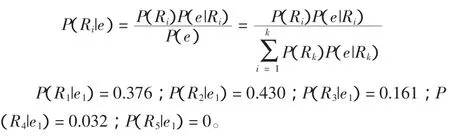
3.3.3 效用函数的求解

考虑资金时间价值后，承包商的效用为Uc′=×+b，这里假设索赔额为承包商实际损失570万元时，承包商的效用为0.6，第一回合讨价还价时t=1，然后已知两点（660，1）（570，0.6）求出承包商的效用函数：

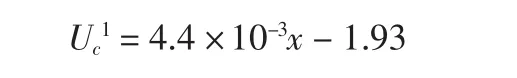
同理求解业主的效用函数，已知两点（480，1）（508，0.6），则：

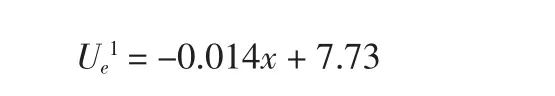
3.3.4 最大风险承受能力的评估

这时承包商的最大风险承受能力要小于业主的最大风险承受能力，所以在下一回合的讨价还价中，承包商要让步，让步的幅度为使业主的最大风险承受能力小于等于承包商的最大风险承受能力。

所以第二回合讨价还价中，承包商的报价为540万元，考虑资金时间价值，此时t=2，承包商的报价为=540.72≈540万元。业主还价500万元。同理可求得

第二回合讨价还价中，承包商的最大风险承受能力小于业主的最大风险承受能力，所以承包商在第三回合报价中会继续让步。

以此类推，继续计算，到第四回合讨价还价中即t=4时，承包商的报价为515万元，考虑资金时间价值的报价为=516.38，承包商在第四回合报价516万元，此时业主还价515万元，这个值很接近承包商的报价，并且高于谈判破裂点索赔额500万元，双方达成一致，最终索赔额为515万元。

本文中资金的时间价值是以银行利率ri和承包商的企业利润率rc考虑进模型中的，随着索赔谈判时间的持续，影响谈判成本的因素还包括谈判双方的效用取向和谈判人员的心理承受能力等等。由于这些因素都与谈判持续时间有关，所以，都可以按照资金的时间价值统一考虑。双方的效用取向在前文中已有涉及，即不同谈判方对相同得益的效用是不同的，比如承包商的效用对得益更敏感，则rc取值要调大。谈判人员的心理承受能力也会影响资金的时间价值，谈判人员心理承受能力较差的一方r取值较大。

4 结语

1）想要得到满意的索赔谈判结果，不论业主还是承包商首先都应对谈判双方有充分的了解，这样才能比较准确的估计出对方的报价；在讨价还价过程中，双方应根据对方的报价修正对对方保留值的估计，这样才能在下一轮讨价还价中正确报价；在考虑了资金的时间价值后，双方会更快达成一致，结束索赔。

2）在索赔谈判中，考虑资金时间价值，包括资金利率、双方的效用取向和谈判人员的心理承受能力等。由于这些都以谈判持续时间有关。所以，都可以按照资金的时间价值统一考虑。资金利率较高，效用对得益较敏感，谈判人员心理承受能力较差时，r取值较大。

3）考虑了以上因素后，谈判双方应采取积极的态度来解决僵持局面，使得谈判双方既得到了可接受的索赔费用，又可以减少谈判成本，达到双赢的目的。

4）由于国际水运工程的资金量巨大，考虑资金时间价值的索赔谈判模型更适合现实情况，对解决索赔期较长、金额较大的水运工程建设索赔问题尤其具有应用价值。

本文建立的水运工程施工索赔谈判模型将资金时间价值作为变量考虑，实现了资金时间价值对索赔谈判的影响程度的量化，为业主、承包商双方如何合理进行索赔谈判提供了参考。

[1]李艳梅，鲁丛林.基于博弈论的BOT项目特许期的决策模型[J].工程经济，2007（3）：22-24.

[2]REN Z，ANUMBA C J.Learning in Multi-agent Systems：a Case Study of Construction Claims Negotiation[J].Advanced Engineering Informatics，2002（16）：265-275.

[3]REN Z，ANUMBA C J.Multi-agent Systems for Constructions Claims Negotiation[J].Journal of Computing in Civil Engineering，2003（1）：180-188.

[4]袁宏川，李慧民.工程合同索赔谈判中的博弈分析[J].工业技术经济，2008（7）：119-122.

[5]LU Wenxue，NIE Jianming.Study of the Dynamic Game in Change Pricing between Owner and Contractor[C].International Conference on Wireless Communications，Networking and Mobile Computing，2008.

[6]NIE Jianming，LU Wenxue，LIU Xuejiao.Research of the Bargaining Process in Construction Claim with Discount Factor[C].Proceedings of the 2009 International Conference on Management and Service Science，2009.

[7]谢识予.经济博弈论[M].上海：复旦大学出版社，2006：348-350.

[8]乐建兵，杨建梅.基于Zeuthen谈判策略的博弈仿真研究[J].科技管理研究，2006（2）：175-179.