基于CORDIC算法的流水线型FFT处理器设计

李靖宇，许江宁，李 豹，曹可劲

(1.海军工程大学 导航工程系，湖北 武汉 430033;2.海军91821部队，广东 潮州 515700)

责任编辑:时 雯

快速傅里叶变换是DSP的核心技术之一，作为时域和频域转换的基本运算，是数字谱分析的必要前提，在雷达、观测、跟踪、高速图像处理、保密无线通信和数字通信等领域有广泛应用。FPGA(现场可编程门阵列)内部含有大量逻辑单元和高速RAM模块，使FFT算法可以灵活快速地实现，并具有很高的性能。针对快速信号处理的要求及FPGA器件的特点，提出了一种基于CORDIC算法的基二流水线结构的FFT处理器设计方法。

1 基二FFT算法原理分析

设序列长度是为N=2M，M为正整数。如此可以将序列x(n)分解成两组，偶数项为一组，奇数项为一组，可以得到两个N/2点的子序列，即:x1(r)=x(2r)，x2(r)=x(2r+1)，r=0，1，…，N/2 －1;相应地将 DFT 运算分为两组［1］。

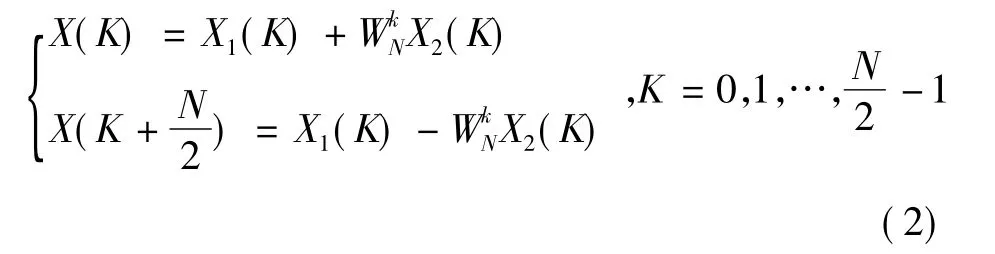
继续照上式将序列分解，直到最后是二点的DFT为止。8点FFT蝶形图如图1所示。

图1 k=8的时间抽取FFT流图

2 基二FFT的FPGA实现

在FPGA上实现流水线型FFT处理器，其主要结构模块包括:输入的乒乓RAM模块、蝶形运算模块、旋转因子乘法模块(本文用CORDIC算法实现)、倒序输出模块、旋转相角(φ)ROM，还有信号流程控制模块和地址产生器模块。具体如图2所示。

图2 FFT硬件实现流程

2.1 RAM的乒乓读取

为了使输入数据无等待周期，采取了乒乓操作。这种结构是将输入数据流不断写入存储深度为2N的存储单元，用RAM写地址值的最高位来区分低、高存储部分，数据首先输入的低位存储区，当低N个存储单元存储满之后，数据开始存入高N个存储单元，同时开始读取低N个存储单元的数据，由于读写频率相同，低存储单元的数据读完后高存储单元已经写满，此时则开始将数据写入低存储单元，读出高存储单元。如此循环往复，一旦RAM存满最初N个数据后，RAM就可以不间断的输出按要求分组的N个数据点。

由于FFT的蝶形运算特性，要求最终输出结果是顺序输出，即:RAM的读地址应该是其同步写地址的低N－1位二进制码的求逆。如此即可将按正常次序存入RAM的数据进行逆序输出。其中RAM写地址和RAM读地址均由地址产生单元产生，而要保证RAM读、写同步速，在进行求逆时不能有延时，因此对求逆运算要采用组合逻辑电路或者是函数运算来实现。

2.2 蝶形运算的实现

由于读入蝶形单元的数据是串行输入的，而蝶形单元涉及到前后不同地址的数据的加减运算，因此必须对先前输出的数据进行寄存，利用两个选择控制信号对输入数据进行运算控制，如图3所示［2］。

在选择器控制信号sel0的控制下选择对输入数据或输入数据与寄存器输出相加的结果进行寄存。当sel0为高电平时选择对输入数据进行寄存，低电平时对输入数据与寄存器输出的数据相加结果进行寄存。sel1信号控制对寄存器输出数据或寄存器与输入数据之差进行输出。移位寄存器深度可表示为2m－1，m为蝶形运算所在的级数。每级蝶形运算都有sel0、sel1两个控制信号，所有控制信号由控制单元产生。sel1信号为sel0取反后的信号，其频率为主控制时钟的2m分频，m为该蝶形所在的级数。每级蝶形运算输出即送往下一级蝶形运算，在输入下一级之前需与旋转因子进行相乘。

图3 蝶形运算实现方法

2.3 利用CORDIC算法实现旋转因子乘法器

旋转因子的获取有两种方法:一种是将先所需要的旋转因子计算预先存储在ROM中，再通过ROM寻址获取后和相应的数据相乘。本文采用的是实时计算的方法，即将需要旋转的角度值预先存储在ROM中，通过ROM寻址将需要旋转的角度送入CORDIC计算器，直接计算出数据与cosφ和sinφ乘积值。实时计算的方法对计算点数不多的FFT，具有很大的灵活性，也可以节省存储空间。

CORDIC 算法的原理如式(3)所示［3－4］:CORDIC算法的流水线实现流程如图4所示。

图4 圆周CORDIC算法流程图

式(3)中(x0，y0)为旋转向量点的坐标值，经过逐步迭代移位相加运算后可以得到式(5)

当旋转向量和x轴重合时，即y0=0时，其最终结果可表示为

表1 预旋转角度表

2.4 地址产生单元与ROM存储设计

地址产生单元主要用来产生RAM的读、写地址和旋转相角ROM的读地址。主要是根据时钟的步速(串行数据的输入步速)产生RAM的写地址，并按照求逆的要求将写地址的低N－1位二进制数按位序求逆产生对应RAM读地址。按照写地址的最高位是1还是0判定读地址的最高位是0还是1，保证其进行乒乓读取。ROM读地址的产生与RAM读地址的产生同步同时产生，但不用求逆，即与RAM写地址的低N－1位完全相同，并以N点为周期进行循环产生。

由于ROM地址产生器产生的地址是与RAM写地址的低位N－1值相等的，即数据开始串行输入蝶形单元的顺序值。而经过蝶形单元运算后产生了数据延迟，等到N个数据完全移出一级蝶形单元时，ROM的地址值已经重新开始计数，由此产生了ROM的循环寻址，即:将相角数据φ预先存入ROM时要考虑延迟后的寻址，ROM地址重新归零后对应的存储单元要存放的数据是对应延迟输出的几个相角值。如此就像循环右移一样，将本应该存储地址末尾的内容拿到存储地址的前几个地址，如图5所示。

2.5 控制信号与数据对准

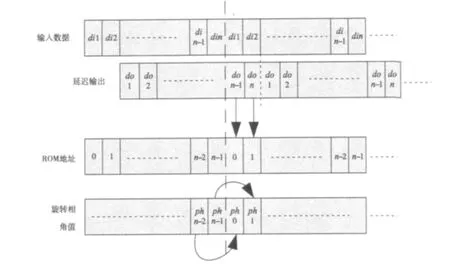
图5 ROM存储设置示意图

在每级蝶形单元的交叉运算中都需要控制信号sel0，sel1，总计需要2M个控制时钟，M为基二运算过程中的蝶形运算中所需的级数。从数据开始输入的同时开始计数、分频，由于每级不同的延迟，数据从第m级输入到输出由于中间有移位寄存器的延迟作用会对数据的输出造成延迟，延迟量可以表述为2m－1，其中2m－1为移位寄存器的深度，读入数据过程中本身就有一个数据延迟，因此第m级的数据输出相对于开始输入蝶形单元的数据总延迟量可以表述为1+2+…+2m－1+2m。而控制数据输出的sel1信号不断经过时钟的2的整数次幂得到的，此时会产生各级输出数据(下级的输入)与下级蝶形运算控制信号的上升沿未能对准的情况，因此需要将各级数据在输出过程中进行不同单位的延迟(增加寄存次数)以保证蝶形单元的输出数据与下级蝶形单元的选择器控制时钟对齐，只有输入数据与蝶形单元的控制时钟的上升沿对准，才能保证数据进行正确的寄存和运算。

在蝶形运算过程中，由于是控制时钟的关系，按照二进制码逆序输入的数据最终在FFT处理器输出是十进制的逆序，即先输出的是第N个数据，最后才输出第一位数据。要得到正确的顺序输出在最后一级蝶形运算后需要进行倒序处理，同样为保证输出的连续性也采取了乒乓操作，只是此时有实、虚两部分数据，存储空间要比输入时的RAM大一倍。

3 仿真与验证

利用MATLAB产生的数据作为FFT的输入激励。设计输入信号为100 kHz与300 kHz的叠加，采样频率为1 MHz，FFT点数定为32，将采样值转换成二进制数据，并写入txt文件，如下文所示:

在testbench中利用verilog语言的系统函数MYM-readmemb将txt文件中的二进制数据读入存储数组datamem，在采样时钟的控制下，将datamem中数据串行读入FFT处理器，作为输入激励，如下文所示:

MYMreadmemb(″binarydata.txt″，datamem)

利用verilog系统函数MYMfdisplay将FFT处理器输出的实部和虚部数据写入txt文件，方便利用MATLAB读取分析。部分代码如下:

利用MATLAB绘图对比分析结果如图6所示。

图6 MODELSIM输出结果验证

对比分析可以证实该设计基本满足了FFT对频谱分析的要求。其幅度值不等是因为在硬件设计中采用了防止溢出的限幅措施。

4 总结

主要讨论了基二FFT在FPGA上的实现方法，结合CORDIC算法，在FPGA芯片上实现了FFT处理器，解决了设计过程中的乒乓读取，CORDIC旋转运算，ROM存储，数据与控制时钟的对准等问题。并进行了MODELSIM和MATLAB的联合仿真，仿真结果表明该设计满足了FFT处理的处理要求。在10 MHz采样率的情况下完成32点的FFT运算需要14.45 μs，满足实时处理的要求，并且具有可以继续扩展到更高的点数，具有推广价值。下一步将考虑更为节约资源的方法，使其用于具体的装备中。

［1］俞卞章.数字信号处理［M］.2版.西安:西北工业大学出版社，2002.

［2］高亚军.基于FPGA的数字信号处理［M］.北京:电子工业出版社，2012.

［3］UWE M.Digital signal processing with field programmable gate arrays［M］.刘凌，译.北京:清华大学出版社，2003.

［4］刘福奇，刘波.Verilog HDL应用程序设计［M］.北京:电子工业出版社，2009.

［5］文婧媛，徐欣锋.基于CORDIC算法的高速可配置FFT的FPGA实现［J］.微电子学与计算机，2010，27(3):24－28.