基于宏观运动波和微观元胞自动机的双车道交通流混合建模

杨海飞 陆 建 祁 玥

(东南大学江苏省交通运输规划与管理重点实验室，南京210096)

宏观交通流模型［1-2］通常被应用于大型城市交通网络的模拟计算，而微观模型则适用于小范围交通节点或路段的仿真.2种空间层次相结合的混合建模方法采用不同空间表现尺度的交通流模型对不同路段或节点进行建模.其中，微观交通流模型［3-5］基于车辆跟驰模型和换道模型来模拟交通流状态演变的微观细节，适用于需要表现微观驾驶行为的路段或节点.宏观模型［1-2］将车流看作可压缩连续流体，通过建立关于车辆密度和空间平均速度的偏微分方程组研究交通流动力学行为，这类模型计算复杂度低，适用于连接由微观模型模拟的路段或节点.混合建模能模拟在需要放大交通流空间表现尺度的路段应用微观层次的模型，有效提高了大型交通流网络的模拟效能.

交通流在宏观/微观交界面上转换的边界条件是混合建模研究的重点，目前相关的研究主要集中在无变道情况下边界条件的定义［6-8］，无变道的混合交通流模型存在局限性:① 现有道路大多是双车道甚至多车道形式，车辆行驶中存在变道行为，无变道的混合模型与实际情况不相符;② 不考虑车辆变道难以充分发挥微观模型在模拟复杂交通流现象时的优越性，进而局限了混合模型的实际应用效果.本文基于宏观运动波(KW)理论和微观线性元胞自动机(CA(L))模型，在交通流供需理论［9］框架下，定义了考虑车辆变道行为和元胞自动机空间离散性影响的边界条件，以保证2种不同空间尺度的交通流模型在边界上连续一致，并通过数值模拟予以验证.

1 宏观、微观交通流模型概述

1.1 双车道KW模型与交通流供需方程组

文献［9］运用Godunov有限差分格式对双车道KW模型进行离散，得到:

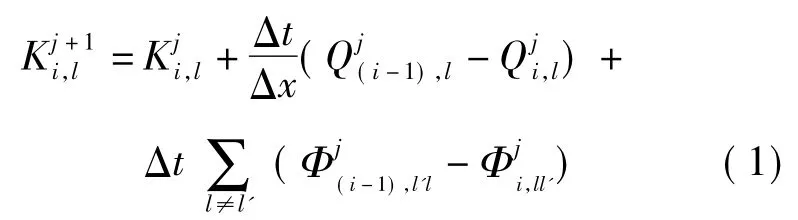
式中，Δx和Δt分别表示空间步长和时间步长;在第 j(tj=jΔt)时刻为车道 l上第 i路段(xi=iΔx)的密度;为进入本车道相邻下一路段的流量，即直行流量;则表示由第i路段进入车道l'第i+1路段的换道流量.

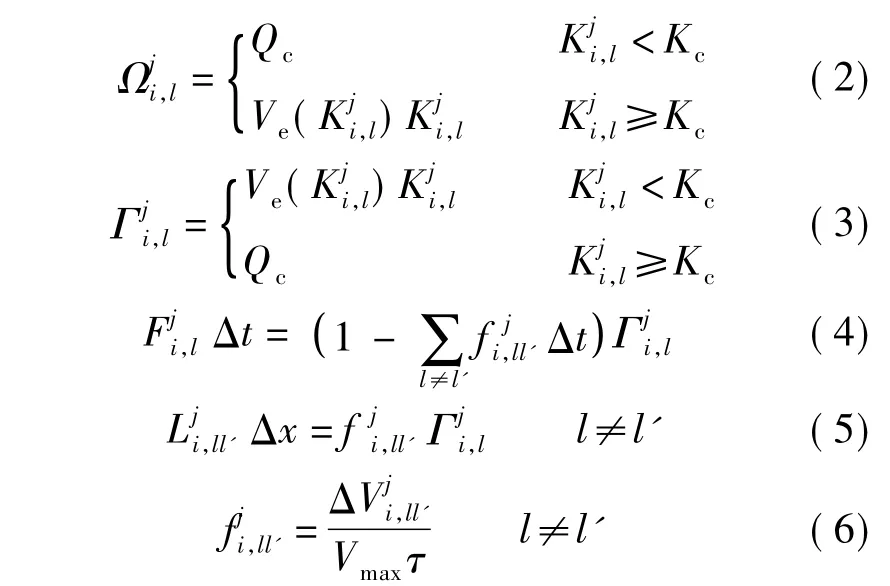
式中，Kc和Qc分别表示临界密度和临界流量;Ve(K)为由基本图确定的密度K所对应的平衡速度;Vmax为畅行速度表示两车道相邻路段的速度差;τ定义为当原车道车流阻塞而目标车道车辆处于自由行驶状态时，原车道驾驶员决定并执行完成变道行为所需的典型时间.

交通流供需理论认为，若路段的供给能力大于所有的期望流入量之和，则所有流量均可进入期望路段，否则实际流入量需按比例减少.因此实际的直行流量和变道流量为

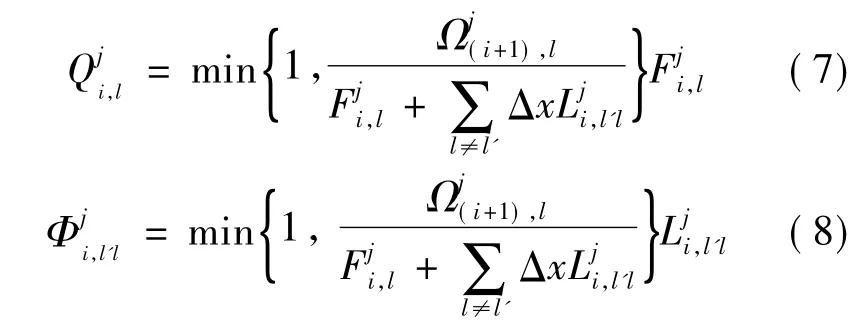
1.2 元胞自动机模型

元胞自动机交通流模型形式简单，且能描述一些复杂的实际交通流现象，因此受到研究者的广泛关注.文献［10］总结了有变道元胞自动机交通流模型的通用更新规则，整个更新过程被划分为2步:①车辆根据变道规则的判断结果，执行变道或继续在本车道行驶.宏观/微观混合建模可以根据具体的道路条件引入符合实际情况的变道模型.例如车辆在即将进入瓶颈路段时，驾驶员变道动机较为强烈，变道是非对称的，阻塞车道车辆的变道概率要远远大于非阻塞车道，此时应用非对称变道规则比对称变道更符合实际的交通状况.②按照独立单车道行驶规则更新车辆位置.

为保证与KW模型的一致性，本文应用线性元胞自动机交通流模型［11］来模拟车辆的行驶轨迹，将道路划分为多个具有一定长度δ的离散网格(即元胞)，每个元胞的状态或者是空，或者是被车辆占据.CA(L)模型的具体更新规则为

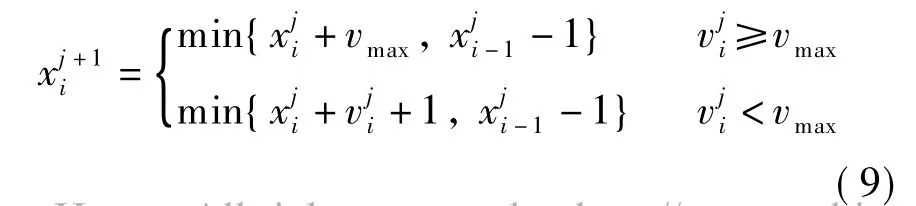
1.3 KW模型与CA(L)模型的一致性分析

文献［11］已经证明，单车道KW 模型在Lagrangian坐标系下应用Godunov有限差分格式求解得到的车辆行驶轨迹与无变道CA(L)模型的模拟结果在一定误差范围内是一致的，并且该误差大小不超过一个堵塞车头间距(即出现堵塞时后车前保险杠与前车前保险杠之间的距离).

在引入车辆变道行为的情况下，KW模型变道车辆的行驶轨迹与CA(L)模型存在差异.双车道KW模型的模拟结果表明，车辆在进入目标车道后会根据当前时刻与前车的车头间距s在下一时刻瞬时加速至平衡速度Ve(s).而在CA(L)模型中，车辆变道后受到本身机动性能限制，在低速状态下渐进加速至平衡速度，这能够合理地刻画变道车辆对目标车道跟驰车流的阻碍作用.

2 混合建模

本文通过拓展文献［7］提出的简单边界条件，定义了考虑车辆变道行为和元胞自动机空间离散性影响的“流量存储”宏观/微观边界转换条件.

所谓“流量存储”方法，就是在宏观/微观边界上，根据交通流供需方程组计算得到边界断面的车流量，并将其存储在流量蓄积变量中，该变量初始值为0，当蓄积变量存储的车流量等于1时，即表示1辆“完整”的实体车完全驶过边界，此时新的实体车辆进入微观路段或微观路段的头车因完全驶入宏观路段而被“销毁”，蓄积变量清零.对该边界条件作进一步修正，以解决由于引入车辆变道行为和应用离散化的微观元胞自动机模型所带来的交通流质量守恒问题:

①车辆变道会导致临近边界上游或下游各车道的密度发生改变，根据交通流供需方程组，这将引起车流量供给或需求的变化.本文在保证流量守恒的基础上，重新计算变道后的车流密度.

②元胞自动机是空间离散模型，临近边界的微观车辆采用向下取整运算更新速度，可能造成车速低于连续空间下的实际行驶速度，进而导致边界流量的损失.本文通过引入存储速度损失的变量，弥补由于车辆速度更新造成的边界流量损失.

2.1 微观-宏观边界条件

2.1.1 无变道情况

假设微观-宏观边界的位置坐标为xm2M(见图1)，车辆n首次成为该车道微观路段头车，位置为xf，此时与边界的间距为sf=xm2M－xf，则在车辆n离开微观路段前，xm2M上游临近路段的密度恒为kf，定义流量蓄积变量c(0≤c≤1)，初始值为c=0.交通流在微观-宏观边界的转换规则为:

①t时刻，根据供需方程组，计算xm2M上游临近路段的期望流量为且xm2M下游第一个宏观路段的供给能力为Ω.

图1 微观-宏观转换边界示意图

2.1.2 有变道情况

对于考虑变道的双车道交通流，在每一车道l的边界上均设置蓄积变量cl，并在无变道边界条件的基础上作以下拓展:

①考虑到与宏观路段变道流量的计算结果保持一致，定义车道l上头车n在t时刻的变道概率为表示车道l微观路段的平均速度，产生随机数p，若p≤pc且满足与目标车道前、后车的安全距离条件，则车辆n变道至车道l'，否则继续在当前车道l上行驶.

②判断当前头车在上一时刻是否行驶在当前车道，若是转③，否则转④.

③根据无变道的边界条件，计算下一时刻流过边界的车流量，更新微观路段车辆位置.

④由于头车变道导致临近边界上游路段的密度kf发生变化，设变道后新的头车位置是xcf，距离边界的间距为scf=xm2M－xcf，蓄积变量的值为cl，为保证流量守恒，临近边界上游路段的密度更新为kf=(1 －cl)/scf，转③.

2.2 宏观-微观边界条件

2.2.1 无变道情况

假设宏观-微观边界的位置坐标为xM2m(见图2)，车辆n首次成为微观路段尾车，其前车位置为xu，与边界间距为su=xu－xM2m，则在车辆n+1生成之前，xM2m下游临近路段的密度恒为ku=s－1u，定义蓄积变量c(0≤c≤1).宏观-微观边界的转换规则为:

①当前t时刻，xM2m下游临近路段的流量供给能力为而上游第一个宏观路段的流量需求为Γ.

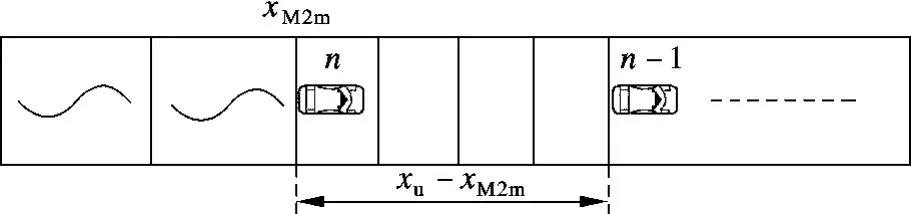
图2 宏观-微观转换边界示意图

2.2.2 有变道情况

与微观-宏观界面类似，对于考虑变道的双车道交通流，在每一车道l的边界上均设置蓄积变量，并在无变道边界条件的基础上作以下拓展:

①同样是考虑与宏观路段变道流量的计算结果保持一致，定义车道l上尾车n在t时刻的变道概率为产生随机数p，若p≤pc且满足与目标车道前、后车的安全距离条件，则车辆n变道至车道l'，否则继续在当前车道l上行驶.

②判断当前尾车在上一时刻是否行驶在当前车道上，若是转③，否则转④.

③根据无变道的边界条件计算下一时刻边界上的车流量并更新微观路段的车辆位置及速度.

④由于变道导致临近边界下游路段的密度ku发生变化，设在t时刻变道后尾车的位置是xcu，与宏观-微观边界的间距为scu=xcu－xM2m，蓄积变量的值为cl，为保证流量守恒，临近边界下游路段的密度更新为ku=(1－cl)/scu，转③.

3 数值模拟

应用宏观/微观交通流混合模型模拟2种常见的双车道交通流现象:① 所有车道在同一位置出现堵塞，并设置堵塞发生在宏观路段;②由于某一车道关闭引起的瓶颈交通流现象，瓶颈出现位置设置在微观路段.通过模拟上述交通流现象，验证混合交通流模型是否具备以下2个关键特征［8］:

1)交通波在经过宏观/微观边界时连续传播;

2)交通流在转换空间表现尺度时质量守恒.

本文应用累计曲线图验证在宏观/微观边界上，微观路段累计生成(离开)的车辆数与宏观路段累计流出(流入)的流量是否吻合.

3.1 宏观路段双车道堵塞

本实验中，车道被划分为300个网格，中间部分第26～275个网格为微观路段，网格长度5 m，其余两侧网格为宏观路段，网格长度25 m;车辆执行变道的典型时间τ=3 s.三角基本图的参数设置为:畅行速度Vmax=20.0 m/s，对应于元胞自动机模型车辆的最大速度vmax=4 m/s，回波速度W=－5.0 m/s，临界密度Kc=0.04 veh/m，临界流量 Qc=0.8 veh/s，阻塞密度Kjam=0.2 veh/m.为满足Godunov有限差分的稳定性条件Δt＜Δx/Vmax，时间步长取为Δt=1 s;给定车道初始密度为K=0.03 veh/m，微观路段车辆占有率为0.15，上游输入流量恒为0.6 veh/s，下游末端的输出流量为0.0 veh/s，造成车流堵塞，采用对称变道规则［9］.

图3(a)显示了宏观路段(空间坐标为0～625 m和1 875～2 500 m的路段)密度随时空变化的趋势以及微观路段(空间坐标为625～1 875 m的路段)车辆行驶轨迹的时空散点图.交通堵塞波在道路下游的宏观路段产生并按照一定速度向上游传播，在经过微观-宏观边界时，微观路段车辆开始出现堵塞，并以相同速度向道路上游蔓延;当微观路段的车辆堵塞到达宏观-微观边界后，导致上游宏观路段密度增大至堵塞密度，堵塞在宏观路段内继续向上游传播.从图中可以看到，交通波能够连续通过宏观/微观边界，传播速度并未出现降低或者振荡现象.

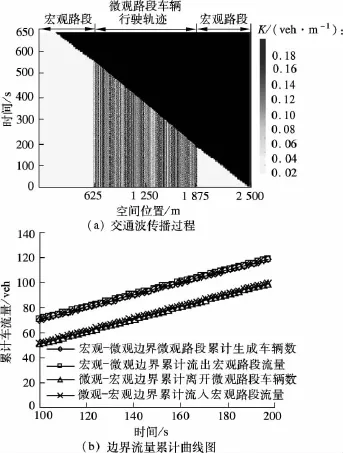
图3 宏观路段双车道拥堵模拟结果

在图3(b)中，随着时间增加，宏观路段累计流出(流入)边界的流量与微观路段累计生成(离开)的车辆数在一定误差范围内是一致的.本实验中平均误差小于0.05 veh，在可接受范围内，从而验证了交通流在经过边界时质量守恒.

3.2 微观路段车道关闭瓶颈

本实验通过模拟瓶颈交通流现象进一步验证混合模型的实际应用效果.实验中微观路段采用UTCA［12］非对称变道规则模拟关闭车道车辆在即将进入瓶颈路段时强烈的变道意愿.车道同样被划分为300个网格，但出现关闭的车道只有上游的225个网格能够通行，其中第1～25个网格为宏观路段，其余200个网格为微观路段.基本图参数和模拟时间步长均与上一实验相同.给定车道的初始密度为K=0.06 veh/m，微观路段车辆占有率为0.3，输入、输出流量恒为0.6 veh/s，数值模拟结果如图4所示.

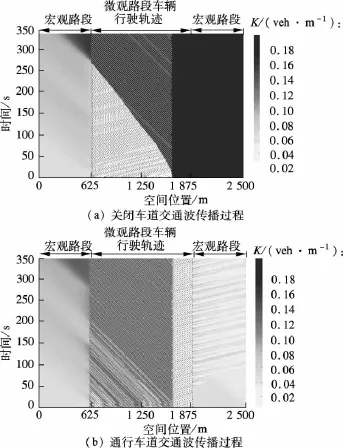
图4 微观路段瓶颈交通流模拟结果

图4(a)中，下游75个网格路段的密度按照致密堵塞设置以模拟车道关闭使车辆不能通行.从图4可以看到，关闭车道上的车辆因前方车道无法通行而在即将进入瓶颈时开始变道至通行的左侧车道，并对原本在通行车道上行驶的车辆造成阻碍.一段时间后两车道在瓶颈位置上游开始出现车辆排队甚至拥堵现象，且此时通行的左侧车道拥堵少于右侧车道，拥堵交通波逐渐传播到上游的宏观路段，而通行车道瓶颈位置下游的车辆行驶轨迹时空图与低密度下单车道的时空散点图接近，下游宏观路段的密度亦较低，这与文献［12］模拟结果一致.另外，本实验模拟结果表明，宏观路段累计流出(流入)边界流量与微观路段累计生成(离开)车辆数在一定误差范围内相一致，误差小于0.05 veh，即交通流在经过边界时质量守恒.

4 结语

宏观/微观交通流混合建模重点需要解决交通流空间尺度发生变化时的连续一致问题，即交通流在经过宏观/微观边界时能够保证质量守恒和交通波连续传播.本文选择宏观KW模型与微观CA(L)模型混合建模，在交通流供需理论的框架下，定义了考虑车辆变道行为和元胞自动机空间离散性影响的“流量存储”宏观/微观边界转换条件.通过模拟常见的交通流现象表明，交通波在模型空间表现尺度发生变化的边界上能够连续传播，并且交通流质量守恒.不同空间尺度相结合的混合建模方法能在需要表现微观驾驶行为的路段应用微观层次模型模拟，有效提高了大型交通流网络的模拟效能.

References)

［1］Lighthill M J，Whitham J B.On kinematic wavesⅠ:flow movement in long rivers［J］.Proceedings of the Royal Society A，1955，229(1178):281-316.

［2］Richards P I.Shocks waves on the highway［J］.Operation Research，1956，4(1):42-51.

［3］Gunay B.Car following theory with lateral dicomfort［J］.Transportation Research Part B，2007，41(7):722-735.

［4］Tanaka K，Nagatani T，Masukura S.Fundamental diagram in traffic flow of mixed vehicles on multi-lane highway［J］.Physica A，2008，387(22):5583-5596.

［5］Li X G，Gao Z Y，Jia B，et al.Deceleration in advance in the Nagel-Schreckenberg traffic flow model［J］.Physica A，2009，388(10):2051-2060.

［6］Bourrel E，Lesort J B.Mixing micro and macro representation of traffic flow:a hybrid model based on the LWR theory ［J］.Transportation Research Record，2003，1852:193-200.

［7］Leclercq L.Hybrid approaches to the solutions of the LWR model［J］.Transportation Research Part B，2007，41(7):701-709.

［8］Leclercq L，Moutari S.Hybridization of a class of“second order”models of traffic flow ［J］.Simulation Modeling Practice and Theory，2007，15(8):918-934.

［9］Laval J A，Daganzo C F.Lane-changing in traffic streams［J］.Transportation Research Part B，2006，40(3):251-264.

［10］Rickert M，Nagel K，Schreckenberg M.Two lane traffic simulations using cellular automata［J］.Physica A，1996，231(3/4):534-550.

［11］Daganzo C F.In traffic flow，cellular automata=kinematic waves［J］.Transportation Research Part B，2006，40(5):396-403.

［12］盛鹏，赵树龙，王俊峰，等.基于元胞自动机模型的道路突发瓶颈现象研究［J］.物理学报，2010，59(6):3831-3840.Sheng Pen，Zhao Shulong，Wang Junfeng，et al.Study of temporary traffic bottleneck based on cellular automaton model［J］.Acta Physica Sinica，2010，59(6):3831-3840.(in Chinese)