M2M网络上的改进直接匿名认证方案

陈立全 何营营 王玲玲

(东南大学信息安全研究中心，南京210096)

机器到机器(machine-to-machine，M2M)网络是当前物联网系统的主要基础架构，它涉及到物联网通信的各方面，包括网络架构、应用案例、终端形态、业务模型及安全体系搭建等［1-3］.随着“智能地球”和“智慧城市”等物联网系统及实现框架的持续推进，M2M系统的用户数量及容量不断提高，怎样有效解决M2M网络上的安全问题显得越来越迫切.因此，3GPP工作组提出了M2M网络上的安全基础架构，将可信计算［4-5］的框架引入到M2M网络之中.

可信计算的核心是可信平台模块(trusted platform module，TPM).而可信计算的一个基本问题是对平台的可信认证.TCG组织在TPM标准v1.1中给出了 Privacy CA 认证方案［3］.Privacy CA 方案简单易行，但也存在2个比较明显的缺点［6-7］.因此，TPM v1.2提出了直接匿名认证(direct anonymous attestation，DAA)方案［8］.但是传统的 DAA方案对于M2M系统中的许多嵌入式设备计算量过于复杂.

本文基于非对称双线性对理论，结合M2M的网络模型和M2M设备的功能结构，针对计算和存储能力较低的嵌入式设备提出I-DAA协议.

1 已有ECC-DAA方案分析

目前主要有以下几种采用椭圆曲线密码算法的ECC-DAA方案:

1)BCL-DAA方案［9］将原始 DAA方案中的基于RSA密码运算修改为对称双线性映射，缩短了密钥长度的同时也降低了算法计算量.

2)CMS-DAA方案［10］将对称双线性对映射改为非对称的双线性对映射.虽然对称双线性映射计算较简单，但是对称双线性对仅能从超奇异椭圆曲线Weil对和Tate对上得到，而非对称双线性对可以从普通椭圆曲线上构造，简单有效.

3)C-DAA方案［11］采用分步验证的思路化简计算量，降低了计算复杂度.

4)ABP-DAA方案［12］希望通过盲化fP1使攻击者不能得到相关的平台隐私信息，进而防止Issuer和Verifier的合谋攻击［12］.但存在以下缺陷:①并未对TPM和Host进行工作量的分配，且在得到证书(A，B，C)之后，TPM 或Host并未对证书进行验证合法性，虽然计算量得到了降低但同时安全性也随之降低.②G1+中的DDH问题是否困难仍有待进一步验证，此方案盲化了fP1，因而，导致TPM参与了证书参数C的计算，增加了TPM的计算量.同时为了防止Issuer和Verifier的合谋攻击，即若TPM 向Issuer提供fP1，则Issuer可以通过验证等式 e(Bi，fP1)=e(Bfi，P1)是否成立来判断出TPM的具体身份，所以对隐私信息f进行了盲化，用fkP1来代替fP1.但是Issuer依然可以通过验证等式 e(Bi，fkP1)=e(Bfi，kP1)是否成立来判断TPM的具体身份.③ 整个协议过程中，没有针对可能发生重放攻击而加入随机质询数或者其他保障机制.④ 没有使用基名，故而不具备申请者(TPM和Host)决定的跟踪可控的性质，灵活性较低.

2 预备知识

2.1 双线性映射及困难性问题假设［11］

假设G1+，G2+是2个加法循环群，G3×是乘法循环群，其阶均为素数 q.G1+，G2+，G3×中的离散对数都是困难的，定义双线性映射为e:G1+×G2+→G3×.它满足以下特性:

1) 双线性.对于任意 P1，P2∈G1+，Q∈G2+，满足 e(P1+P2，Q)=e(P1，Q)e(P2，Q).e(aP，bQ)=e(P，Q)ab，其中 a，b∈.

2) 非退化性.存在 P1∈G1+，P2∈G2+使得e(P1，P2)≠1，其中1 为 G3×的幺元.

3) 可计算性.任取 P1∈G1+，P2∈G2+，存在有效算法来计算e(P1，P2).

上述映射如果G1+=G2+，则称此映射为对称双线性映射，否则称为非对称双线性映射.

1)DL(discrete logarithm)假设 对于P∈G1+或G2+，给定aP，计算a是困难的.

2)CDH(computing Diffie-Hellman)假设 对于P∈G1+或 G2+，给定 aP，bP，计算 abP是困难的.

3)DDH(decisional Diffie-Hellman)假设 对于 P∈G1+或 G2+，区分三元组(aP，bP，abP)和(aP，bP，cP)是困难的.

2.2 基于非对称双线性映射的C-L签名原理［10］

基于非对称双线性映射步骤为

1)密钥生成.任意 P2∈G2+，选取 x，y∈作为签名私钥，计算 X=xP2，Y=yP2，公开参数(P2，X，Y).

2)签名.对于 A∈G1+，计算B=yA，C=(x+mxy)A，其中m为需要签名的消息，对于m的签名为(A，B，C).

3)验证.如果等式e(A，Y)=e(B，P2)和等式e(A，X)e(mB，X)=e(C，P2)成立，则(A，B，C)就是对于m的签名.

3 I-DAA(improved-DAA)方案

3.1 DAA协议主体

DAA协议中共有Signer(签名者)、Issuer(证书颁发者)、Verifier(验证者)3个角色，其中Signer被拆分成TPM和Host.由于本文是基于M2M网络模型的可信匿名认证机制，一般将Issuer和Verifier归由同一个实体扮演.故本文中并不考虑证书颁发者和验证者的合谋攻击.但为了便于与已有的DAA方案进行统一和比较，本文仍用不同的名字命名.

3.2 系统参数建立

Issuer选择有限域Fq上一可构造非对称双线性对的普通椭圆曲线.e:G1+×G2+→G3×为非对称双线性映射.选取x，y∈Fq作为其私钥，对于P2∈G2+，P1∈G1+.计算 X=xP2，Y=yP2，A=P1，B=yP1，H1，H2，H3，H4，H5为哈希函数，其参数可参考文献［11］.其中，(pk，sk)为TPM 的EK公私钥对，{0，1}*和{0，1}t分别表示任意长度和长度为t的二进制串.(pk，X，Y，A，B，H1，H2，H3，H4，H5，P1，P2)为公开参数，私有参数为(x，y，sk).Rougelist为已经泄漏f值的TPM名单及其对应的f值.

3.3 证书申请

I-DAA方案的证书申请过程主要由TPM，Host和Issuer来完成，如图1所示.Issuer选取随机数nI∈{0，1}t，并用TPM 的公钥加密得到M=E(pk，nI)，发送给TPM.TPM 用对应的私钥解密得到nI=D(sk，M).TPM 选取f∈Fq作为其秘密信息并计算D=fB.将(D，nI)发送给 Issuer.Issuer首先比较nI是否正确，然后查看此TPM是否在Rougelist上.对于任意 fi∈Rougelist，如果 D=fiB，则此f已经泄漏，认证失败.否则计算DAA证书中的参数，即

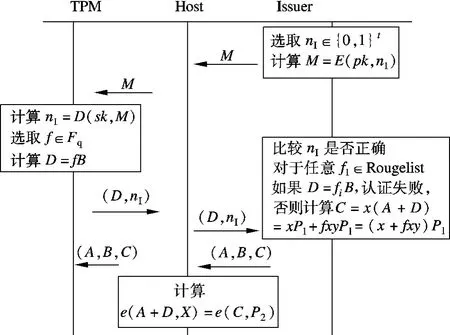
图1 I-DAA的证书申请流程图

式中，(A，B，C)即为Issuer颁发给TPM 的DAA证书.收到证书后，TPM通过计算比较算式e(A+D，X)=e(C，P2)是否相等，来验证证书的正确性，完成双向认证.

(A，B，C)即为申请到的DAA证书.本过程中只需验证由Issuer在Join过程生成的C.与文献［11］中的C-DAA方案相比，可让Host减少计算2次双线性映射.Issuer用TPM的EK公钥加密随机数，从而保证只有合法的TPM才能获得证书，即用随机数来抵御重放攻击.

3.4 基于DAA证书的签名

I-DAA方案中的证书签名过程如图2所示.Verifier产生随机数 nV∈{0，1}t发送给 Signer.bsn为Signer的基名，若方案允许签名关联即bsn=⊥，则选 J∈G1+，否则令 J=H3(bsn).选取 l∈Z*q，计算R=lA，S=lB，T=lC和G=lD(此步计算是将证书进行盲化，进一步增强其匿名性)以及E=H4(R‖S‖T‖G‖nV).Host将 J，S，E 发送给TPM，由TPM 进行签名.首先TPM 选取 nT∈{0，1}t，r∈Z*q，并计算 Z=rS 和 m=H5(J‖nT‖E‖Z‖PCR)，PCR为平台配置，其中 a=r+fm(modq).最后，Host把基于DAA证书的签名σ=(m，nV，nT，R，S，J，T，G，a)发送给验证者 Verifier，等待验证.

图2 I-DAA的证书签名流程图

I-DAA方案在签名过程中依然使用随机质询数来抵抗重放攻击，用哈希函数来保证信息完整性，防止篡改攻击.由于Host计算的R，S，T与证书(A，B，C)有关，所以可以提前计算以缩短认证时间.通过使用基名bsn可以实现由TPM控制的关联性检测，实现可选的不同安全级别，应用更加灵活.

3.5 签名验证

I-DAA方案的签名验证部分的工作流程由Verifier完成.

Verifier收到签名后，首先进行 Roguelist检测，然后检验基名bsn的使用是否正确，最后验证签名合法性.通过计算Z'=aS－mG=(r+fm)S－mG≡rSmodq，用匿名认证方法保证了TPM的合法性.在验证等式e(R+G，X)=e(T，P2)和e(R，Y)=e(S，P2)时可参考文献［10］，选取 e1，e2∈Zq，将以上 2个等式等价为计算 e(［e1］R，Y)e(［－e1］S，P2)e(［e2］(R+G)，X)e(［－ e2］T，P2)=1是否成立.这个转换将4个独立的双线性映射转换成了4个映射的变形加上4个乘法运算.改进后的方法可节省40%的计算量.对Verifier的验证流程为

若通过以上所有步骤，则本次验证通过.

4 I-DAA方案的安全性分析

I-DAA方案解决了以上各种问题.首先，IDAA方案对TPM和Host的计算工作进行了清晰的分配，由于TPM的资源比Host宝贵得多，所以应尽可能地将计算量由TPM向Host转移，由Host分担很多计算负担，进一步减轻TPM的计算量.其次，I-DAA方案中的Host并没有得到TPM的关键信息f，从而无法在没有TPM辅助的情况下伪造证书，从而保证了强匿名性.最后，I-DAA方案在签名过程的信息中加入了随机数以防止重放攻击，而且I-DAA方案使用了基名，具有申请者可控的特性，增加了方案的灵活性.与 C-DAA［11］等方案相比，I-DAA方案在相同的安全性和匿名强度下降低了计算复杂度.

4.1 正确性

I-DAA方案的正确性在于验证等式e(A+D，X)=e(C，P2)，e(R，Y)=e(S，P2)以及 e(R+G，X)=e(T，P2)是否成立.验证的过程为

由双线性映射的双线性性质可知，上述等式成立，从而验证了I-DAA方案中签名的正确性.

4.2 安全性

可以证明I-DAA方案在没有泄露其秘密信息f值及证书的情况下是安全的.假设攻击者可以自己伪造证书 A，B，C'，D'(A，B 是公开参数)，且 C'= αP1，D'= βP1.则伪造者可以选择 l'∈Zq计算 R=l'A，S=l'B，R=l'A，S=l'B，显然其可以通过等式e(R，Y)=e(S，P2)的验证.因为 e(R+G，X)=e(T，P2)=e(l'P1+l'βP1，xP2)=e(l'αP1，P2)，即 e(P1，P2)(1+β)xl'=e(P1，P2)αl'，所以(1+β)x=α，这意味着可以通过 D=βP1，X=xP2来计算 C=(1+β)xP1，但这是 co-CDH问题［5］，即此假设不成立.对于中间人攻击，假设攻击者截获了合法签名 R，T，U，S，选取 r∈Zq重新计算出 R'=rR，T'=rT，G'=rG 和 S'=rS，虽可以通过 e(R，Y)=e(S，P2)，e(R+G，P2)=e(T，P2)的验证，但这会导致E值的变化，从而验证失败.

4.3 关联性可控

I-DAA方案使用了基名bsn，可以实现TPM可控的关联性检测.若TPM想被验证者Verifier关联，则使用相同的基名bsn，而Verifier可以通过发现相同的J而确认是同一个TPM.

5 I-DAA方案的效率分析

通过与文献［11］提出的C-DAA方案和文献［12］提出的ABP-DAA方案进行比较来分析IDAA方案的效率.这些方案均包含证书申请、证书签名、证书验证这3个过程中涉及到的计算量，但并没有包括相对于计算较容易的非对称加解密、单向散列函数的运算量，也没有包含Setup过程以及其中参数的验证的计算量，因为这些运算只需做一次.

用下列符号表示方案中各种运算及参数:对于双线性映射 e:G1+×G2+→G3×:G1+为群 G3×中的运算，如P∈G1+计算aP;G21+为群G1+或G2+中的运算，如 P，Q∈G1+，计算 aP+bQ;G×为群 G3×中的运算，如 P∈G3×计算 Pa;G2×为群 G3×中的运算.如P，Q∈G3×，计算 PaQb;P为双线性映射运算，如 P1∈G1+，P2∈G2+计算 e(P1，P2);n 为黑名单中已经泄露了f值的TPM的个数.

根据上述设定，得到以下各方案的效率开销数据，见表1.表中，方案ABP-DAA在Join过程中的Host的计算量是0，这是因为申请者没有对证书的合法性进行验证;G+/2G1+表示允许/不允许基名关联时的计算量.

表1 各方案的计算开销对比

通过对比可知，I-DAA方案既较大地降低了Signer(TPM和Host)的计算复杂度，又降低了在申请和签名过程中TPM的计算量.与Host和Verifier相比，TPM的计算资源要更宝贵.

6 结语

基于非对称双线性映射，延续了已有的基于双线性映射的DAA认证方案的流程，在已有方案的基础上，结合M2M的系统结构，提出了一种改进的直接匿名认证方案——I-DAA方案.在保证安全的前提下有效降低了计算复杂度，因而更适用于M2M网络中嵌入式设备.由于I-DAA方案基于M2M网络的特点，因此目前暂无需考虑合谋攻击问题.

References)

［1］Wu G，Talwar S，Johnsson K，et al.M2M:from mobile to embedded internet［J］.IEEE Communications Magazine，2011，49(4):36-43.

［2］Sun Wenchao，Song Meina.A general M2M device model［C］//IEEE 2nd Symposium on Web Society.Beijing，China，2010:578-581.

［3］Potter B.High time for trusted computing［J］.IEEE Security ＆Privacy，2009，7(6):54-56.

［4］Kim Mooseop，Ju Hongil，Kim Youngsae，et al.Design and implementation of mobile trusted module for trusted mobile computing［J］//IEEE Transactions on Consumer Electronics，2010，56(1):134-140.

［5］Chen Liqun，Warinschi B.Security of the TCG Privacy-CA solution［C］//IEEE/IFIP 8th International Conference on Embedded Ubiquitous Computing.Hong Kong，China，2010:609-616.

［6］Li Lixin，Li Chaoling，Zhou Yanzhou.A remote anonymous attestation scheme with improved privacy CA［C］//International Conference on Multimedia Information Networking and Security.Wuhan，China，2009:153-157.

［7］Brickell E，Camenisch J，Chen L Q.Direct anonymous attestation［C］//Proceedings of the 11th ACM Conference on Computer and Communications Security.New York，USA，2004:132-145.

［8］Brickell E，Chen Liqun，Li Jiangtao.A new direct anonymous attestation scheme from bilinear maps［C］//Proceedings of First International Conference on Trusted Computing and Trust in Information Technologies.Villach，Austria，2008:166-178.

［9］Chen Liqun，Morrissey P，Smart N P.Pairing in trusted computing［C］//Second International Conference on Pairing-Based Cryptography-Pairing. Egham，UK，2008:1-17.

［10］Chen Liqun.A DAA scheme using batch proof and verification［C］//Proceedings of Third International Conference on Trust and Trustworthy Computing.Berlin，Germany，2010:166-180.

［11］Chen Liqun，Page D，Smart N P.On the design and implementation of an efficient DAA scheme［C］//International Conference on Smart Card Research and Advanced Application.Passau，Germany，2010:223-237.

［12］甄鸿鹄，陈越，谭鹏，等.基于非对称双线性对的直接匿名认证方案［J］.通信学报，2010，21(7):56-62.Zhen Honghu，Chen Yue，Tan Peng，et al.Asymmetric bilinear pairing based direct anonymous attestation scheme［J］.Journal of Communications，2010，21(7):56-62.(in Chinese)