基于效能分析的网络可靠性评估模型

姜 禹 胡爱群

(东南大学信息科学与工程学院，南京210096)

网络可靠性分析涉及到现实网络系统的设计、维护及修复，正在受到越来越多的关注.网络系统的部件都有一定的内在失效概率，部件的失效会导致网络无法完成预先设定的任务.因此，如何定量评价一个网络的可靠性具有重要的意义.IEEE 90标准将可靠性定义为“某个系统或部件在规定状态和时间下能执行其功能的能力”［1］.

目前，网络可靠性的评价方法通常使用如下的常用网络模型，通信网用图G=(V，E)表示，为无自环的无向连通图，其中，V={x1，x2，…，xn}表示网络中的 n 个节点集合，E={e1，e2，…，em}表示网络中的m条链路集合.每条链路和每个节点的失效是随机和相互独立的，并具有一个已知的失效概率.网络可靠性的评价方法通常用于研究两终端可靠性［1-2］、多终端可靠性［3-4］及全网可靠性［5］等问题.上述问题的分析是假定网络的链路和节点具有固定的可靠性，通过布尔代数和概率论得到网络的可靠性值.

在实际网络系统中，对于不可修复系统，网络部件经历可靠性下降的过程，直到损坏和失效;对于可修复系统，故障后会进入修复过程，在正常运行和失效2种状态之间转换.有些研究者［6-8］提出了基于可修复网络的稳态可靠性分析方法，在得到网络部件稳态可靠性的情况下求得网络的稳态可靠性.

对于固定可靠性和稳态可靠性的网络分析，仅通过固定的或稳态的可靠性值是无法有效地评估网络的，这是因为网络的可靠性与网络的运行时间密切相关［9-10］.本文在故障率模型的基础上提出了链路和节点效能的概念，建立与时间相关的效能模型，并根据全网可靠性方法得到整个网络的时间效能模型，通过网络效能的变化动态评价网络的可靠性.

1 效能模型

1.1 初始故障率模型

随着硬件组件可靠性的提高，其MTBF(mean time between failure，平均无故障时间)也在不断增加.CPU、内存、硬盘等都具有以年为单位的可操作生命期.但是当这些硬件组件集成起来组成网络中的链路(光缆、电缆等)和节点(工作站、PC、路由器等)时，集成系统的MTBF定义为［11］

式中，Rk为系统中组件k的MTBF;N为系统中的组件数量.直观上可以看出，最不可靠的组件决定了整个系统的可靠性.尽管硬件组件的可靠性不断提高，但系统的集成度也在不断加大，即使组件中个体的可靠性非常高，由式(1)可知，大量的系统组件也会造成系统可靠性的下降.

1.2 使用期故障率模型

在网络部件正式使用前，必须经过试用或老化过程，以便筛选合格的网络部件.大量的网络部件同时启动，由图1可见，在起初的0～t0时间内，无网络部件失效，故障率为0;在t0～t1时间内，网络部件失效较多，但故障率α逐渐下降，这个阶段就是部件的试用或老化过程;在t1～t2时间内，网络部件失效的较少，故障率α接近常量，这可作为正常使用期;在t2以后，失效的组件又较多，故障率α上升，这是衰竭期.在实际应用中，这时网络部件已超过正常使用寿命，应予更换，以保证系统的正常运作.

图1 网络部件故障率的时间曲线

为了能定量描述图1的曲线，使用Weibull函数表示故障率曲线α(t)，即

式中，a，b，c为形状系数，可以根据实际测量某时刻的故障率计算获得.α由α(t)在t1处的连续性获得，即

1.3 节点和链路效能模型

在实际网络中，节点和链路效能指节点和链路当前能完成网络任务的能力占其最大有效能力的比值，部件效能与部件的故障率密切相关.节点的效能表现为节点处理能力的大小，链路的效能表现为链路所承担流量的大小.

不可修复系统中，根据系统可靠度定义方法［12］，定义效能为

若故障率α与t无关，则

根据故障率α(t)的表达式(2)，得到效能函数为

现实网络系统中，部件经过老化期和试用期后，进入正常使用期.以此时的部件效能E(t1)=1，作为考虑部件效能变化的起点.

对于可修复系统，根据系统可靠度定义方法［12］，定义效能为

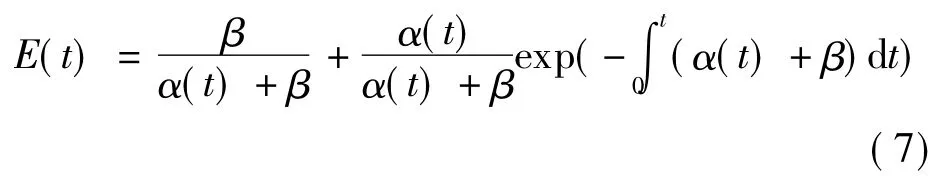
式中，β为修复率，与时间无关.如果α与t无关，则从式(7)可得到E的稳态效能为

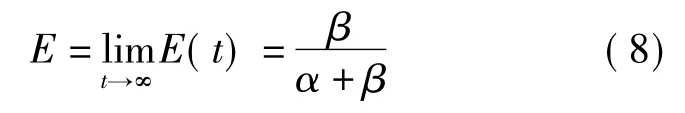
实际应用中，α与t相关且满足式(2)的故障率模型，则E的稳态效能为

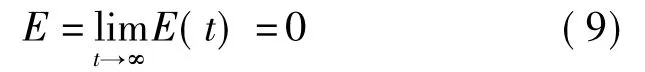
1.4 网络效能模型

本文采用常用的网络模型表示方法来分析网络效能，而计算网络效能的前提是网络有效.网络有效指网络中的所有节点能够通过有效链路进行通信.网络效能由网络中节点和链路效能经过拓扑关系获得.网络效能EN(t)表示为

式中，Ev(t)为网络总的节点效能，网络有效必须保证网络中的节点均有效.当网络中的某个节点效能为0，则网络失效.因此，Ev(t)可以表示为

式中，Evi(t)为节点i的效能;n为网络中的节点个数.

Ee(t)是网络总的链路效能，网络有效必须保证网络中i条链路有效且与所有节点相连，其中i≥n－1.因此，Ee(t)可以表示为

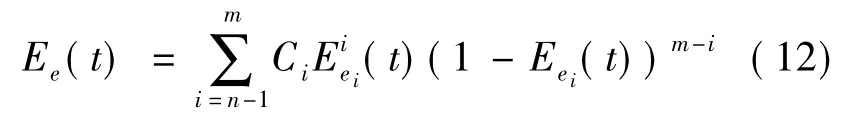
式中，Ci表示i条链路连接所有节点且其余m－i条链路无效的网络状态个数;Eei(t)为链路i的效能.当链路效能Eei(t)与时间无关，且将Eei(t)用链路可靠性pi代替时，则式(12)等价于在节点完全可靠的前提下求解固定可靠性的全网可靠性问题.

2 应用实例

对于不可修复系统，利用图2给出的无向网络G1 对本文算法进行说明.节点 vi(i=1，2，3，4)表示网络终端，其MTBF由其组件的MTBF共同决定.假设组件包括CPU(C)、硬盘(D)、主板(M)、内存(R)，它们的MTBF分别为RC=5×105，RD=1 ×105，RM=2 ×104，RR=1 ×105.由式(1)得节点vi的MTBF为

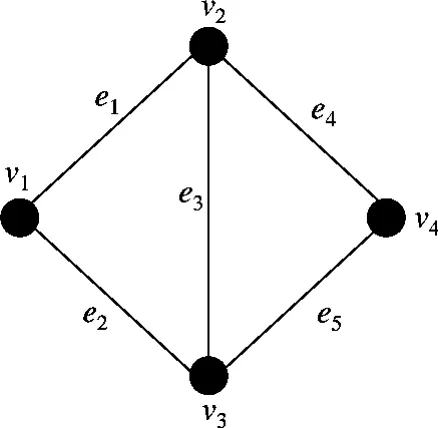
图2 无向网络G1

在故障率时变系统中，Rvi为节点正常使用期的 MTBF，t1为起始使用点，此时节点效能为Evi(t1)=1，t2时刻进入衰竭期，根据式(2)得到节点故障率表达式为

根据式(6)和(13)，得到时变系统的节点效能表达式为

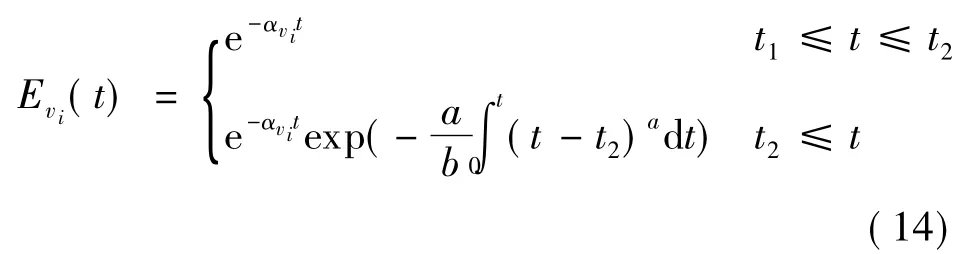
在故障率时不变系统中，由式(5)得

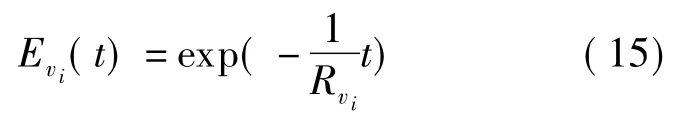
根据式(14)和(15)分别得到故障时变和时不变系统的节点效能曲线(见图3).

根据可靠性理论中的节点MTBF定义［13］，时变故障系统中的节点效能曲线更接近于现实模型.

边ei(i=1，2，…，5)作为网络中的通信链路，其MTBF受到交换机处理能力、链路线缆质量等因素的影响，这里假设链路的MTBF为 Rei=1×104.对于故障率时变系统，αei=1/Rei，a=1.5，c=500，由式(3)得当 t1=0，t2=7 000 h 时，

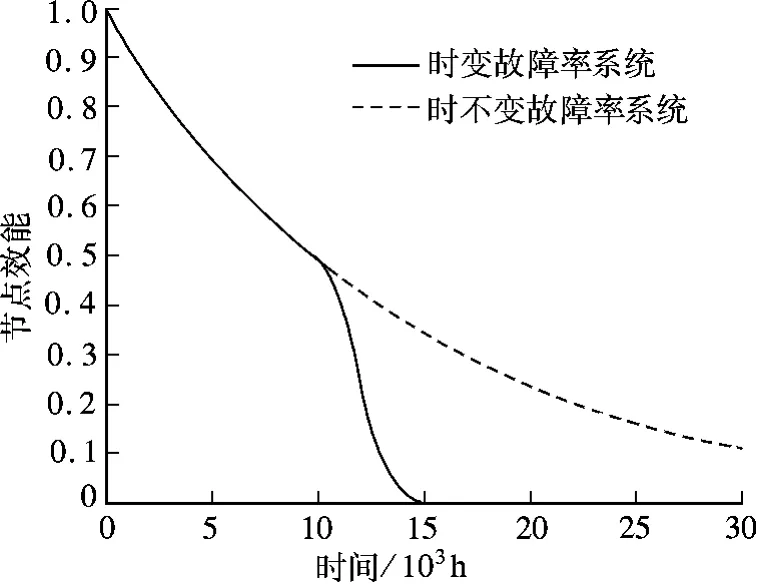
图3 节点效能随时间的变化曲线(t1=0)

根据式(2)得到链路的故障率表达式为

根据式(5)和(6)可分别得到故障时不变和时变系统的链路效能表达式为

假设链路和节点均服从统一的效能模型，根据式(11)得到图2中网络G1总的节点效能为

根据式(12)得到网络G1总的链路效能为

采用文献［14］中的方法，可以得到C3=8，C4=5，C5=1，则

当链路服从统一的效能模型时，可以根据全网可靠性的求解方法得到总的链路效能Ee(t)的表达式，目前最有效的算法为文献［3］提出的BDD算法.

根据式(10)得到网络效能为

图4(a)为 1.5Rvi，1.5Rei，10Rvi和 10Rei下时变和时不变故障率系统的网络效能随时间变化曲线.由图可以看出，当R较小时，即MTBF较小时，2种故障率系统描述的网络效能随时间的变化基本一致，但当R较大时，2种故障率系统描述的网络效能随时间的变化出现了很大差别，时不变故障率无法描述网络部件进入衰竭期的效能变化，时变故障率更加接近现实网络系统.随着部件MTBF的提高，时变故障系统更加适合于实时的网络效能分析.

图4 网络效能随时间的变化曲线

下面分析可修复系统中网络效能随时间的变化，假设链路和节点均服从统一的效能模型，失效部件失效后马上进入修复状态.对于时变故障率系统，节点和链路的故障率曲线和不可修复系统中的曲线相同，分别由式(13)、(7)以及式(16)、(7)得到节点和链路的效能表达式.其中MTTR(mean time to restoration，平均修复时间)是MTBF的1/4，节点和链路的修复率分别为 βvi=4αvi，βei=4αei.图4(b)为 1.5Rvi，1.5Rei，10Rvi和 10Rei下时变和时不变故障率系统的网络效能随时间变化的曲线.由图可以看出，对于故障率时不变系统，网络效能随着时间增长将趋于稳定值.而对于故障率时变系统，随着时间的增长，网络效能将趋于0.对于实际网络系统，当部件进入衰竭期后，其效能必定趋于0，这样使得整个网络效能为0.因此，时变故障系统模型更准确地刻画了网络效能随时间的变化.

3 结语

本文在故障率模型的基础上提出了链路和节点效能的概念，建立了与时间相关的效能模型.并根据全网可靠性方法得到整个网络的时间效能模型，根据网络效能的变化动态评价了网络的可靠性.实例分析说明，本文提出的网络效能模型客观描述了网络效能随时间的变化，为网络可靠性分析提供了更加有效的方法.

References)

［1］Gebre B A，Ramirez-Marquez J E.Element substitution algorithm for general two-terminal network reliability analyses［J］.IIE Transactions，2007，39(3):265-275.

［2］Satitsatian S，Kapur K C.An algorithm for lower reliability bounds of multistate two-terminal networks［J］.IEEE Transactions on Reliability，2006，55(2):199-206.

［3］Yeh F M，Lu S K，Kuo S Y.OBDD-based evaluation of k-terminal network reliability［J］.IEEE Transactions on Reliability，2002，51(4):443-451.

［4］Hardy G，Lucet C，Limnios N.K-terminal network reliability measures with binary decision diagrams［J］.IEEE Transactions on Reliability，2007，56(3):506-515.

［5］Younes A，Girgis M R.A tool for computing computer network reliability［J］.International Journal of Computer Mathematics，2005，82(12):1455-1465.

［6］刘爱民，刘有恒.可修复网络稳态可用度分析［J］.通信学报，1997，18(7):15-19.Liu Aimin，Liu Youheng.On the steady-state availability of repairable network［J］.Journal on Communications，1997，18(7):15-19.(in Chinese)

［7］刘爱民，刘有恒.关于可修复系统的MTBF和MTTR［J］.电子学报，1998，26(1):70-72.Liu Aimin，Liu Youheng.On the MTBF and MTTR of repairable system［J］.Acta Electronica Sinica，1998，26(1):70-72.(in Chinese)

［8］Shi Jian，Wang Shaoping.Integrated availability model based on performance of computer networks［J］.Reliability Engineering＆System Safety，2007，92(3):341-350.

［9］Braverman J I，Miller C A，Hofmayer C H，et al.Degradation assessment of structures and passive components at nuclear power plants［J］.Nuclear Engineering and Design.2004，228(1/2/3):283-304.

［10］Torres M A，Ruiz S E.Structural reliability evaluation considering capacity degradation over time［J］.Engineering Structures，2007，29(9):2183-2192.

［11］Reed D A，Lu C D，Mendes C L.Reliability challenges in large systems［J］.Future Generation Computer Systems，2006，22(3):293-302.

［12］周炯槃.通信网理论基础［M］.北京:人民邮电出版社，1991:20-33.

［13］王少萍.工程可靠性［M］.北京:北京航空航天大学出版社，2000:89-110.

［14］Neufeld E M，Colbourn C J.The most reliable seriesparallel networks［J］.Networks，1985，15(1):27-32.