基于MD-CM-SFLA神经网络的耳语音情感识别

张潇丹 包永强 奚 吉 赵 力 邹采荣

(1东南大学水声信号处理教育部重点实验室，南京210096)

(2南京工程学院通信工程学院，南京211167)

在禁止大声喧哗的部分场所中，耳语音是人们进行语言交流的主要方式之一.耳语音的早期研究主要停留在语音基础研究和医学工作需要上.随着科学技术的快速发展，关于耳语音的研究开始转向其他方面，如耳语音的语音增强研究［1］、耳语音的语音识别研究［2-3］等.传统的耳语音信号识别仅限于语义信息的识别而忽略了情感信息的识别.耳语音情感识别的研究是对语音情感识别的有效补充，具有广泛的应用前景.目前，世界上关于耳语音情感识别方面的研究还很欠缺，可以借鉴已有的语音情感识别的研究成果来进行耳语音情感识别研究;但是由于发音特点的独特性，其识别方法与语音情感识别还是有所区别的.

BP神经网络具有很强的鲁棒性和自学习自适应性，适用于处理复杂的、具有非线性和不确定性的对象.近年来，利用群智能优化算法来优化神经网络参数的方法备受关注.文献［4］利用混合蛙跳算法(SFLA)来优化BP神经网络，进行语音情感识别，并证实其识别结果优于BP神经网络.但是SFLA算法［5-7］在进化后期搜索速度慢且出现早熟收敛现象，对于多峰值函数寻优这种较复杂的问题，很难搜索到最优解.针对SFLA算法存在的缺点，本文提出了一种基于分子动力学模拟与云模型理论的改进混合蛙跳算法(MD-CM-SFLA);然后将其与BP神经网络相结合，设计出一种MD-CMSFLA神经网络，并将其应用到耳语音情感识别中.实验结果表明，MD-CM-SFLA神经网络能够明显提升耳语音情感识别率.

1 MD-CM-SFLA算法

1.1 基本原理

根据SFLA算法的更新策略可知，最差个体可在局部最优个体或者全局最优个体的吸引下，不断朝着更优的方向进化;其余个体并不对最差个体的进化产生任何影响.因此，在分子动力学模型中仅需要考虑最差个体和最优个体之间的吸引力;它们之间的距离越大，吸引力就越强.将种群中的青蛙个体等效成分子，仅考虑当前迭代中子群体的最差个体Xw与全局最优个体Xg之间的吸引力，该吸引力随距离的增加而增强.两分子间的作用力可表示为

式中，λ为比例系数;r为Xw和Xg之间的位移矢量则表示分子间距离.假设各分子的质量m相等且为1，则最差个体的加速度矢量为

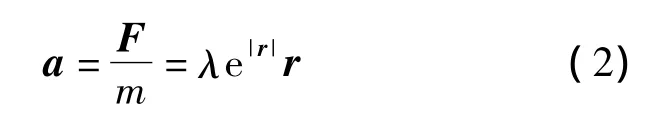
选择Swope等［8］提出的Velocity-Verlet算法来求解更新后最差个体的位置、速度和加速度，可得

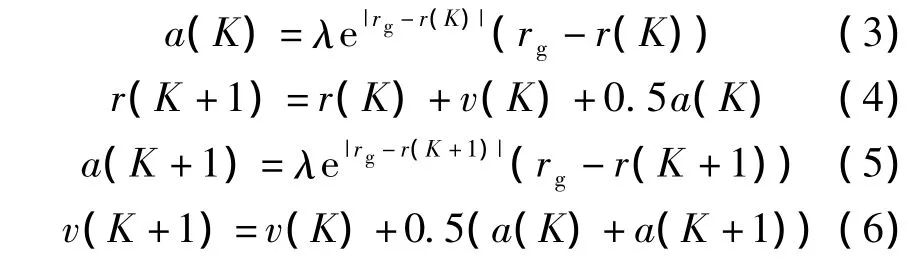
式中，r(K)，v(K)和a(K)分别表示当前时刻最差个体的位置、速度和加速度;r(K+1)，v(K+1)和a(K+1)表示更新后最差个体的位置、速度和加速度;rg表示全局最优个体位置.

云模型是一种自然语言值表示的定性概念及其定量数据之间的不确定性转换模型，主要反映了客观世界事物或人类知识中概念的模糊性和随机性［9］.正态云模型是一个遵循正态分布规律、具有稳定倾向的随机数集.云模型的数字特征可用期望Ex、熵En、超熵H三个数值来表征，它们反映了定性概念的定量特性.生成云滴的算法称为云发生器.基本云发生器的算法步骤如下:①生成一个以En为期望值、H为标准差的正态随机数E'n;②生成一个以Ex为期望值、E'n为标准差的正态随机数x;③ 计算y=exp(－(x－Ex)2/(2(E'n)2)).(x，y)完整地反映了这一次定性定量转换的全部内容.

本文将Velocity-Verlet算法引入到SFLA算法中，采用式(3)～(6)作为局部深度搜索的更新策略.同时，引入具有随机性和稳定倾向性的云模型理论，利用基本云发生器来代替原更新策略中的随机更新操作，提出MD-CM-SFLA算法.其具体步骤如下:

①随机初始化青蛙种群和青蛙个体的速度变量，设置MD-CM-SFLA算法参数.

②计算每只青蛙个体的适应度值.

③将当前所有青蛙个体按照适应度值从优到劣进行排序，并划分子群体.

④对当前子种群的最差个体Xw按照式(3)～(6)进行更新.如果更新后的个体适应度值优于更新前，则用更新后的个体取代更新前个体Xw;反之，则利用正态云发生器生成新个体.其中，Ex=Xw;En=Ω/c1，Ω表示变量搜索范围;He=En/c2，c1，c2均为常数.

⑤当所有子种群完成以上的更新操作后，若满足全局混合迭代次数，进化过程结束，输出全局最优值;否则，将全部的青蛙个体重新混合，转至步骤③.

对于c1和c2的取值范围，文献［9］进行了分析.借鉴其分析结果，取c1为种群大小，c2=10.

1.2 收敛性证明

定理1MD-CM-SFLA算法的种群序列{tk，k≥0}是有限齐次马尔可夫链，其中k表示迭代次数.

证明本文中初始化种群是有限的，且算法中的更新策略均与迭代次数无关，因此tk+1仅与tk有关，即{tk，k≥0}是有限齐次马尔可夫链.证毕.

定理2MD-CM-SFLA算法的马尔可夫链序列的种群最优值序列是单调不减的.

证明在MD-CM-SFLA算法中，只有最优个体的适应度值超过原最优个体时，原最优个体才会被取代，这样保证了每代拥有的最优个体都不差于前一代.证毕.

定理3MD-CM-SFLA算法以概率1收敛.

证明设种群为状态空间S中的某个点，sj∈S为S中的第j个状态，f为S上的适应度函数，f∧为全局最优值为最优解集.MD-CM-SFLA算法的状态转移由马尔可夫链来描述表示处于状态 sj的第k代种群 tk，随机过程{tk}的转移概率设 I=，由定理2 可得

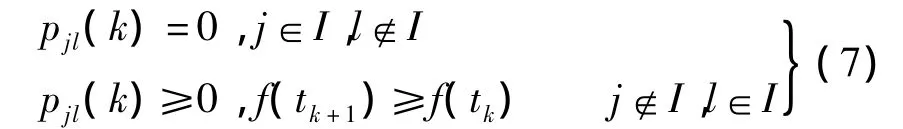
设pj(k)为种群tk处于状态sj的概率，由马尔可夫链的性质可得

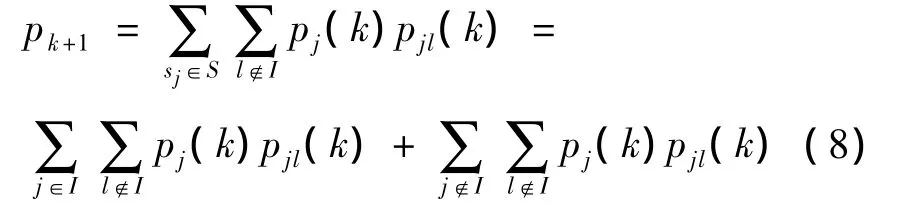
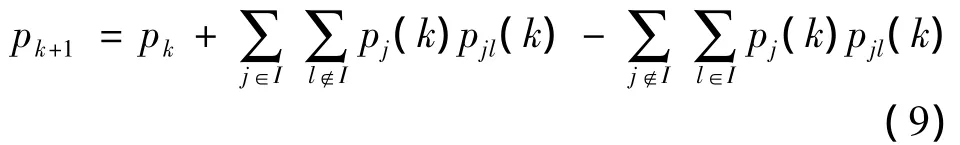
1.3 数值仿真实验

为了验证MD-CM-SFLA算法的优化性能，采用国际上常用的4种标准测试函数Sphere函数、Griewank函数、Ackley函数和Rastrigin函数对其进行性能分析，函数的具体表达式参见文献［10］.然后，对比了MD-CM-SFLA算法、SFLA算法和文献［10］中MMT-PSO算法的优化性能.其中，MDCM-SFLA算法的参数设置如下:种群规模为200，子群体规模为20，子群体数为10，局部深度搜索迭代次数为20，全局混合迭代次数为150，比例系数为4.SFLA算法中优化Ackley函数时全局混合迭代次数为200，优化其他3种函数时为1 000，其余参数同MD-CM-SFLA算法.为了验证参数变化对算法性能的影响，分别将维数取为10，20，30，对每个函数独立运行50次.3种算法的寻优结果比较见表1.表中的平均值表示50次独立实验所得解的平均适应度值;标准差反映了算法的稳定性.图1为MD-CM-SFLA算法和SFLA算法的函数寻优对比图，图中A表示平均最优适应度值.

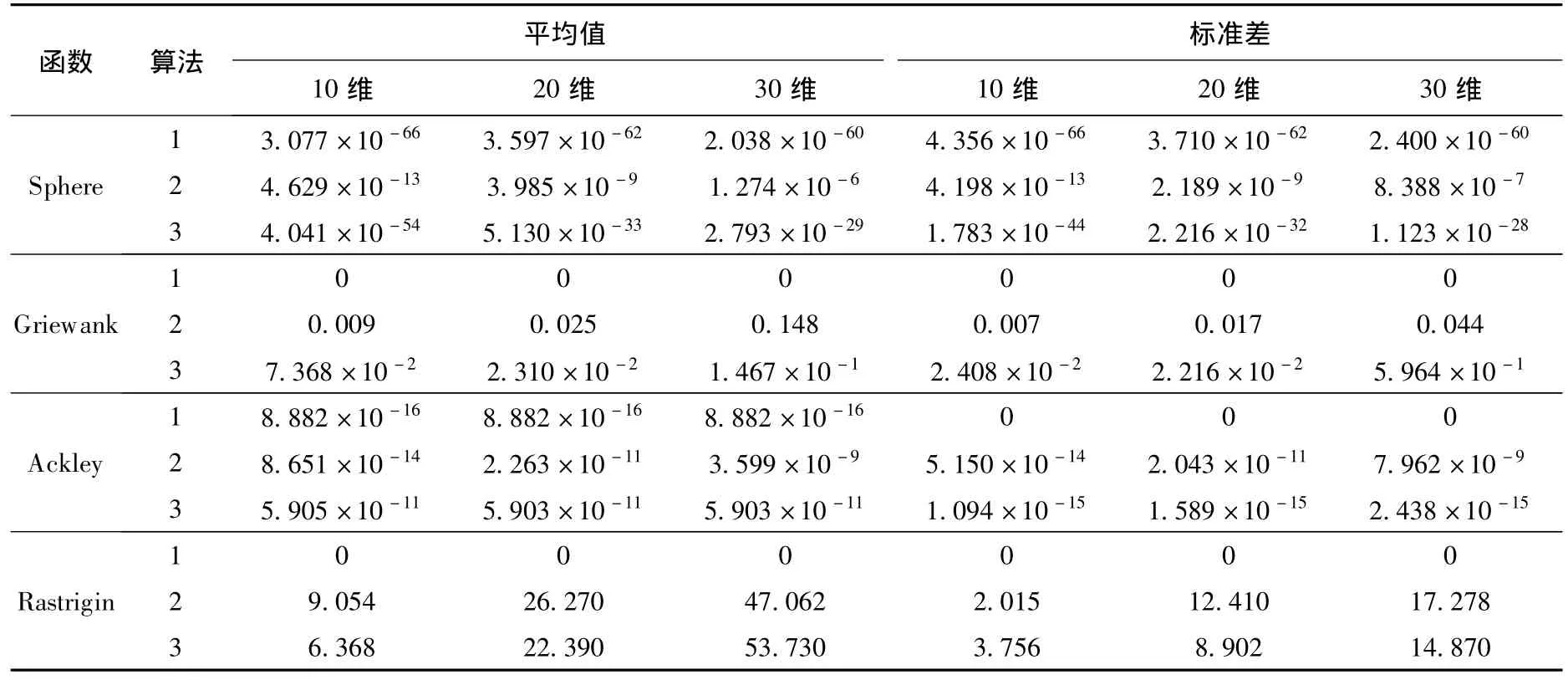
表1 3种算法寻优结果比较

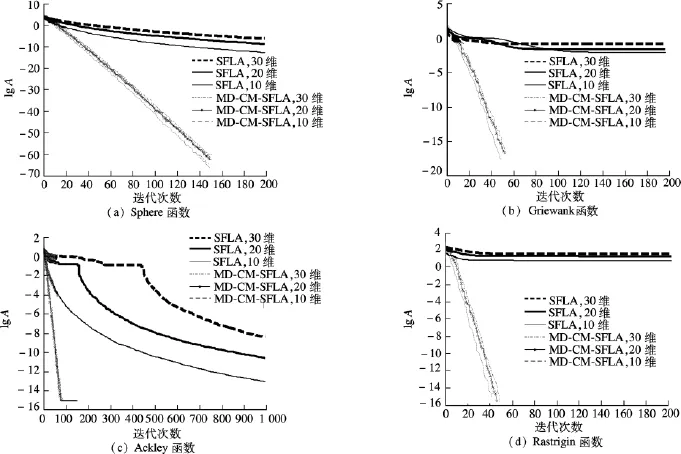
图1 2种算法的函数收敛曲线对比图

图1反映了算法的收敛过程.由表1可知，在相同的求解维数下，MD-CM-SFLA算法的求解精度和稳定性明显优于其他2种算法.结合表1和图1可知，随着维数的增加，算法的优化性能逐渐变差，这是因为求解维数的增加导致搜索空间变大，算法更易陷入局部最优.对于MD-CM-SFLA算法而言，求解维数的变化对其优化性能的影响不大，表明算法对于参数不敏感，易于使用.由图1可知，MD-CM-SFLA算法的收敛速度和求解精度明显优于SFLA算法.在图1(b)和(d)中，MD-CM-SFLA算法的收敛曲线出现截断，表示已搜索到全局最优解，而SFLA算法则出现早熟现象.由此可知，MDCM-SFLA算法的各项改进机制使算法具有高效的搜索性和跳出局部极值的能力;与SFLA算法相比，MD-CM-SFLA算法具有更强的全局搜索能力、更高的搜索精度、更快的收敛速度和更好的鲁棒性.

2 MD-CM-SFLA神经网络

BP神经网络常用的学习算法是BP算法.该算法是基于梯度信息来调整连接权值的，因而极易陷入局部极值点，而且在高维输入时，易出现“维数灾”问题，影响收敛速度.本文提出的MD-CMSFLA算法是一种群体智能优化算法，其全局优化性保证了算法可以有效地对解空间进行搜索，不易陷入局部最优，能够快速收敛，寻优精度高，而且算法具有较强的通用性，对问题的具体形式和领域知识依赖性不强，其固有的并行性保证了算法能够较快地寻找到最优解或满意解.因此，在进行BP神经网络训练时，本文使用MD-CM-SFLA算法对网络的随机初始参数、输入层与隐含层的连接权值、隐含层与输出层的连接权值以及各阈值进行优化，从而提高了神经网络的收敛速度和学习能力.具体的训练步骤如下:

①随机初始化青蛙种群.每个青蛙个体中的维数信息依次表示输入层与隐含层的连接权值、隐含层与输出层的连接权值以及各阈值.

②计算个体的适应度值.适应度函数定义为

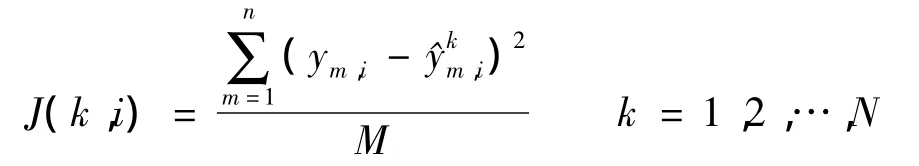
式中，J(k，i)为第i个个体第k次迭代后的适应度值;M为训练集的样本数;ym，i为第i个个体中第m个样本输入时的网络目标输出值为第 i个个体第k次迭代后第m个样本输入时的网络实际输出值;N为最大迭代次数.

③采用MD-CM-SFLA算法的迭代寻优步骤对青蛙个体进行更新.当进化过程结束时，返回全局最优解，训练结束.

3 耳语音情感特征

3.1 耳语音情感数据库的建立

目前，对耳语音情感识别的研究还处于初级阶段.参照国际著名语料库建立的规范，以表演的方式获取耳语音情感数据，创建一个包括高兴、生气、悲伤和平静的耳语音情感数据库.录音选择在安静的实验室内进行，采样频率为16 kHz.共10名大学生参与录制，其中5名为男性，5名为女性.录音语料分为单词、短句和段落3种类型.其中，单词包括名词和动词各10个;短句包括陈述句19句，疑问句、感叹句和祈使句各2句;段落6个.语料都具有比较高的情感自由度，每位表演者用耳语音对所有语料分别重复3遍，再用正常音朗读1遍(用于后期对比).通过听辨实验，保留1 250条语句作为训练和测试所用的数据库.

3.2 耳语音情感特征参数提取

耳语音和正常音的发音方式有所不同.耳语音中塞音、塞擦音和清擦音的声母部分与正常音的发音方式基本类似;但元音和浊辅音在发音时，不产生声带振动、没有基频，这与正常音的发音方式不同.因此，适用于正常音情感识别的一些特征参数并不适合进行耳语音情感识别.目前，关于耳语音声学特征参数的分析主要集中于音高、能量、声调、共振峰、音长、Mel域参数、语速等方面.本文主要提取的用于耳语音情感识别的特征参数包括音长、语速、基于TEO变换后的4种改进的12阶MFCC、第1，2，3共振峰的均值、最大值、最小值、中值和标准差.

4 耳语音情感识别实验

本实验从数据库中总共选取了1 000条语句(高兴、生气、悲伤和平静4种情感各250条)，其中训练语句200条(4种情感各50条)，识别语句800条(4种情感各200条).采用OCON方法组织神经网络结构，每种待识别的情感对应一个子神经网络模型，将所有子神经网络的输出结果通过判决策略，产生最终的识别结果.令每个子神经网络的输出为vz，分别采用每种情感对应的情感语料对子神经网络进行训练，输出值为每种情感的似然函数，最终的输出结果可判决为z*=argmax(vz)，其中z*为语音情感类别.基于BP神经网络和MDCM-SFLA神经网络的耳语音情感识别结果分别见表2和表3.

表2 基于MD-CM-SFLA神经网络的耳语情感识别率 %

表3 基于BP神经网络的耳语情感识别率 %

由表2和表3可知，MD-CM-SFLA神经网络的平均识别率为77.5%，而BP神经网络的平均识别率为72.3%，表明MD-CM-SFLA神经网络的学习能力明显优于BP神经网络.在所考虑的4种情感中，耳语音对高兴、悲伤、平静情感的识别率相对较好.悲伤、生气情感容易出现相互误判，且识别率不理想，而这2种情感和高兴情感出现误判的情况相对较少.高兴、生气这2种情感在激活维上坐标接近，在效价维上则距离较远，说明识别这2种情感时只要将对应于效价维的特征参数选择恰当，便可获得高的识别率.反观生气、悲伤2种情感，它们在效价维上坐标接近，在激活维上则距离较远，因此识别这2类情感时需要有合适的激活维参数.本文在识别中所采用的特征参数主要是效价维参数.由于耳语音发音方式的特殊性，不存在基音这一重要的激活维参数，因此在识别生气、悲伤这2种情感时效果不理想.

5 结语

本文针对SFLA算法在进化后期存在早熟收敛的缺陷，通过分子动力学模拟种群的进化策略，结合正态云模型云滴的随机性和稳定倾向性特点，提出了一种MD-CM-SFLA算法，并从数学上证明了该算法的全局收敛性.将该算法与BP神经网络相结合，设计出一种MD-CM-SFLA神经网络，并将其应用于耳语音情感识别中.实验结果表明，MD-CM-SFLA神经网络相对于BP神经网络具有明显的优势，在相同的测试条件下，其平均识别率较BP神经网络提高5.2%.由此表明，利用MDCM-SFLA算法优化神经网络学习的权值和阈值，可以快速地实现网络的收敛，获得较好的学习能力.

References)

［1］Tao Zhi，Zhao Heming，Wu Di，et al.Speech enhance-ment based on modified mel masking model and speech absence probability in whispers ［J］.Acta Acustica，2009，34(4):370-377.

［2］王敏，赵鹤鸣，张庆芳.基于瞬时频率估计和特征映射的汉语耳语音话者识别［J］.数据采集与处理，2011，26(6):686－690 Wang Min，Zhao Heming，Zhang Qingfang.Speaker identification with Chinese whispered speech based on instantaneous frequency estimation and feature mapping［J］.Journal of Data Acquisition ＆Processing，2011，26(6):686-690.

［3］Wang Min，Zhao Heming.Whispered speaker identification based on multiband demodulation analysis and instantaneous frequency estimation ［J］.Acta Acustica，2010，35(4):471-476.

［4］余华，黄程韦，张潇丹，等.混合蛙跳算法神经网络及其在语音情感识别中的应用［J］.南京理工大学学报，2011，35(5):659-663.Yu Hua，Huang Chengwei，Zhang Xiaodan，et al.Shuffled frog-leaping algorithm based neural network and its application in speech emotion recognition［J］.Journal of Nanjing University of Science and Technology，2011，35(5):659-663.(in Chinese)

［5］Alireza R V，Ali H M.Solving a bi-criteria permutation flow-shop problem using shuffled frog-leaping algorithm［J］.Soft Computing，2008，12(5):435-452.

［6］Eusuff M M，Lansey K E.Shuffled frog-leaping algorithm:a mimetic meta-heuristic for discrete optimization［J］.Engineering Optimization，2006，38(2):129-154.

［7］Alireza R V，Ali H M.A hybrid multi-objective shuffled frog-leaping algorithm for a mixed-model assembly line sequencing problem ［J］.Computers＆ Industrial Engineering，2007，53(4):642-666.

［8］Swope W C，Andersen H C，Berens P H，et al.A computer simulation method for the calculation of equilibrium constants for the formation of physical clusters of molecules:application to small water clusters［J］.Journal of Chemical Physics，1982，76(1):637-649.

［9］戴朝华，朱云芳，陈维荣，等.云遗传算法及其应用［J］.电子学报，2007，35(7):1419-1424.Dai Chaohua，Zhu Yunfang，Chen Weirong，et al.Cloud model based genetic algorithm and its application［J］.Acta Electronica Sinica，2007，35(7):1419-1424.(in Chinese)

［10］徐星，李元香，姜大志，等.一种基于分子动理论的改进粒子群优化算法［J］.系统仿真学报，2009，21(7):1904-1907.Xu Xing，Li Yuanxiang，Jiang Dazhi，et al.Improved particle swarm optimization algorithm based on theory of molecular motion［J］.Journal of System Simulation，2009，21(7):1904-1907.(in Chinese)