无变压器光伏并网逆变器抑制漏电流的控制策略

宋平岗，沈友朋

（华东交通大学 电气与电子工程学院，江西 南昌 330013）

1 引言

太阳能光伏并网发电系统是有效利用新能源的重要手段之一，在分布式发电系统中也占有很重要的地位。随着各国政府对新能源利用的重视和鼓励，这种发电方式在实际应用中越来越普遍［1］。

传统的光伏并网逆变器一般都会采用带变压器式的逆变器，包括在逆变器输出端接工频变压器和在逆变器输入端接高频变压器2种。虽然接变压器可以实现电压调整和电气隔离的作用，但也存在一些固有的缺点和不足，如工频变压器存在体积大、重量重、成本高以及安装、运输困难等缺点；而高频变压器虽然体积小，结构简单，但因采用多级结构使系统控制复杂，转换效率低。为了去掉笨重的工频变压器和复杂的高频变压器，国外一些学者提出了无变压器光伏并网逆变器的并网系统［2］。因系统中没有变压器，大大提高了整个并网系统的效率，但同时也带来了一些新的问题，如共模电流（在实际光伏并网设备中俗称“漏电流”）、向电网注入直流分量等［3－5］。本文只对共模电流的相关问题进行分析和研究。

由于在无变压器光伏并网逆变器中没有变压器的隔离作用，电网与光伏阵列存在直接的电气连接，而光伏阵列和地之间存在虚拟的寄生电容，因此形成了由寄生电容、滤波元件和电网阻抗组成的共模谐振回路［6］。寄生电容上变化的共模电压在这个共模谐振回路中就会产生相应的共模电流（即漏电流），如图1所示。

图1 无变压器型光伏并网系统的结构框图Fig.1 Transformerless PV system block diagram

无变压器光伏并网系统中的共模电流会带来很多问题和危害，如引起并网电流的畸变、对其他设备产生电磁干扰等，更为严重的是会对人身安全构成重大威胁［7］。因此一些国家对漏电流的要求进行了相关规定，如德国的VDE－0126－1－1标准规定，漏电流超过300mA时，光伏并网系统必须在0.3s内与电网断开。因此漏电流抑制技术已成为无变压器光伏并网逆变系统中必须要跨越的技术障碍。本文主要是从抑制漏电流的控制策略角度，对漏电流的产生原因，以及各种调制方法对抑制漏电流效果的影响进行分析研究，并在此基础上提出、总结了一些抑制漏电流的控制策略。

2 漏电流产生原因的分析

2.1 单相全桥式逆变器的共模分析

图2为单相无变压器全桥式逆变器的拓扑结构。在该拓扑结构中，输出点a，b对o点的电位是由4个开关管控制的，当1个桥臂的上开关管开通时，a（或b）点对o点的电位即为直流侧光伏阵列的输出电压；而下开关管开通时，a（或b）点对o点的电位就为零。这样，光伏阵列和开关管的综合作用就可等效为在ao和bo两端加入2个以开关管频率变化，幅值为光伏阵列输出电压的等效方波电源。因此，单相全桥式拓扑就可等效为如图3所示的简化示意图。

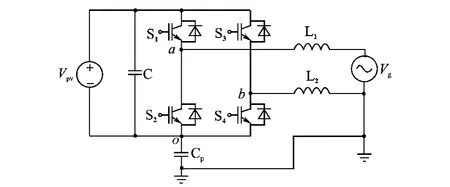
图2 单相全桥拓扑结构Fig.2 Single－phase full－bridge topology

因电网电压频率比开关频率低很多，所以电网电压产生的共模电流可忽略。由戴维南叠加定理，根据图3分别计算2个方波电源单独作用时的共模电流。

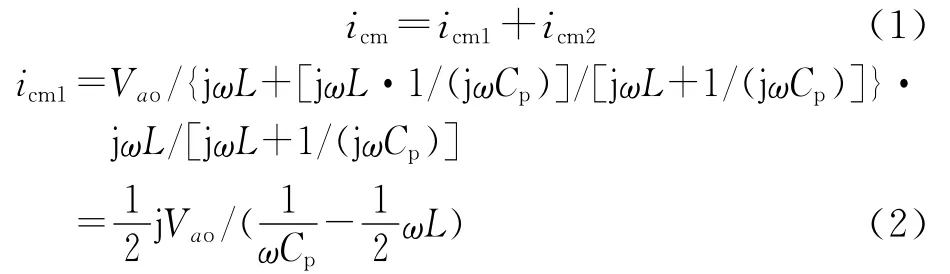
同理可得

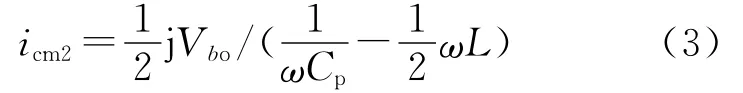
式中：icm为各共模电流之和；icm1为等效电源Vao单独作用时的共模电流；icm2为等效电源Vbo单独作用时的共模电流；ω为开关频率；L为输出滤波电感；Cp为等效寄生电容。

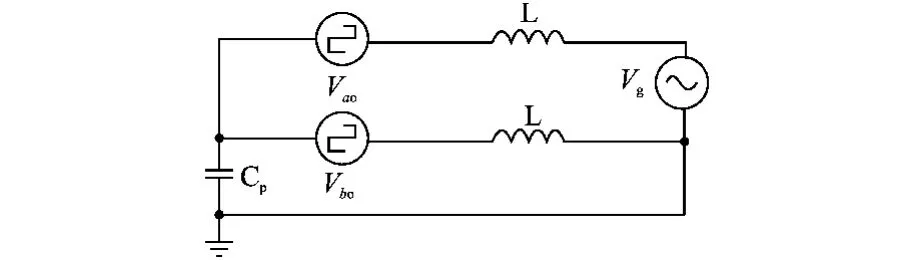
图3 单相全桥式拓扑简化示意图Fig.3 Simplified diagram of single－phase full－bridge topology

等效方波电源单独作用电路如图4所示。

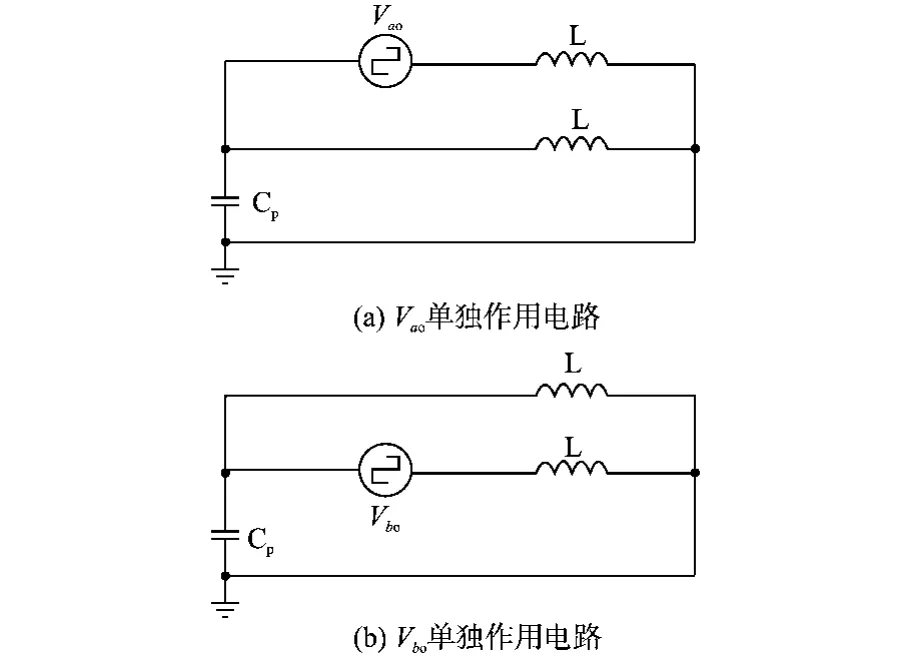
图4 等效方波电源单独作用电路图Fig.4 Circuit of equivalent square wave power alone

对式（2）、式（3）利用叠加定理，将2个等效方波电源叠加在一起，形成如图5所示的单相全桥式拓扑的共模电流分析模型图。图5中，因共模电流比差模电流要小得多，因此在分析共模电流时可忽略电感上的压降。

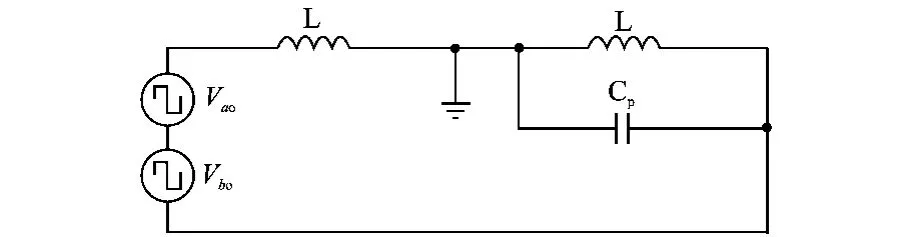
图5 单相全桥电路共模电流模型Fig.5 Common mode current model of single－phase full－bridge circuit

由图5可得共模电流

一般定义共模电压Vcm为

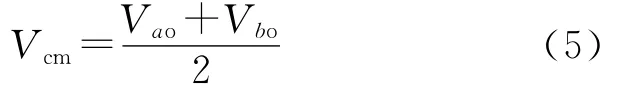
由图5可知，根据式（4）、式（5）可得：当共模电压Vcm为一定值时，共模电流icm为零。

所以，要想抑制共模电流，就必须使得Vcm的变化率保持恒定，使Vcm为一定值，也即使得a，b点对o点的电压之和满足：

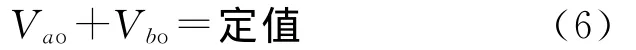
2.2 三相全桥式逆变器的共模分析

图6为三相无变压器全桥式逆变器的拓扑结构。为了方便分析共模电流，定义Vpv为等效光伏阵列的直流电压，VAN，VBN，VCN分别为全桥逆变器交流输出点A，B，C对直流母线N 点的电压，Vcm－AB为A 相与B 相间的共模电压，Vcm－BC为B相和C相间的共模电压，Vcm－CA为C相和A 相间的共模电压，VL为滤波电感上的压降，Vcm为寄生电容Cpv上产生的共模电压，icm为共模电流，Vg为电网电压。

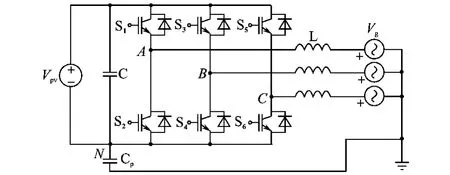
图6 三相全桥拓扑结构Fig.6 Three－phase full－bridge topology

以电网电流的正半周为例，分析全桥式拓扑的共模电流。当开关管S1，S4和S6开通时，在开关管S2，L，Vg和寄生电容Cpv构成的回路以及在开关管S4，L，Vg和寄生电容Cpv构成的回路中，根据基尔霍夫电压定律，可列出共模谐振回路的电压方程：

因Vg为工频电网电压，所以Vg在寄生电容上产生的共模电流一般可忽略，而VAN，VBN为PWM控制的高频脉冲电压，共模电流主要由此激励产生。所以由式（7）、式（8）相加可得A相与B相间的共模电压Vcm－AB为

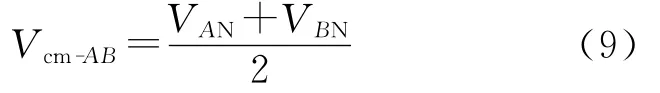
同理可得：B相和C相间的共模电压Vcm－BC为

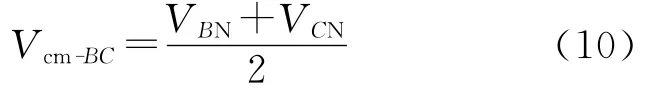
C相和A相间的共模电压Vcm－CA为

由式（9）、式（10）、式（11）3式可得，三相全桥拓扑结构的共模电压Vcm为

而流过寄生电容的共模电流icm为

由式（12）、式（13）可知，要想抑制共模电流，就必须使得Vcm的变化率保持恒定，使Vcm为一定值，即使得A，B，C点对N 点的电压之和满足：

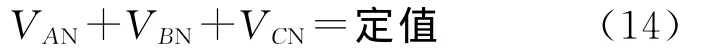
由上述分析可知，不管是单相无变压器光伏并网逆变器系统，还是三相无变压器光伏并网逆变器系统，其共模电流（也即漏电流）的产生均与共模电压有关。由式（6）和式（14）可知，只要保证共模电压Vcm为一定值时，那么共模电流就基本为零。因此可以通过采用不同的拓扑结构或控制策略方式使共模电压为一定值，从而达到有效抑制漏电流的目的。

3 单相无变压器光伏并网逆变器系统的控制策略

由上节分析可知，对于无变压器光伏并网逆变器系统来说，只要保证共模电压为一定值，就可有效抑制漏电流。但是采用不同的调制策略对漏电流抑制效果的影响有相当大的差异。对于单相无变压器光伏并网逆变器系统来说，一般采用3种PWM调制策略，即单极性调制、双极性调制和混合型调制。下面以单相全桥式拓扑结构为研究对象，分别进行讨论。

3.1 单极性PWM调制

图2所示的单相全桥拓扑采用单极性PWM

调制法控制时，在整个工作周期内，开关管S1，S2均按工频调制，而S3，S4均按开关频率的PWM调制。以电网电流正半周为例：

当开关管S1，S4导通，开关管S2，S3关断时，

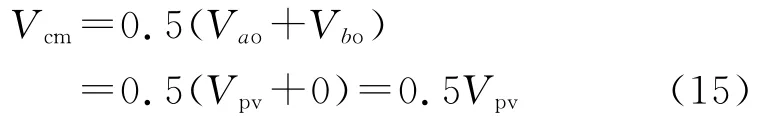
当开关管S1，S3关断，开关管S2，S4导通时，

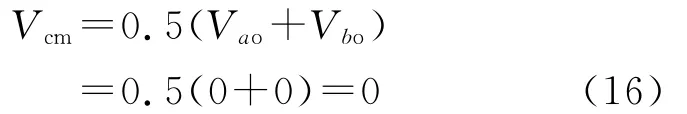
负半周开关管控制顺序与正半周相似。由式（15）、式（16）可知，在开关过程中，共模电压Vcm的幅值是变化的。因此，其共模电流很大，远远超过标准要求。图7为其共模电压Vcm和共模电流icm的波形。由图7可知，在开关过程中共模电压Vcm的幅值是在0，Vpv／2和Vpv之间变化的。因此共模电流的值很大。

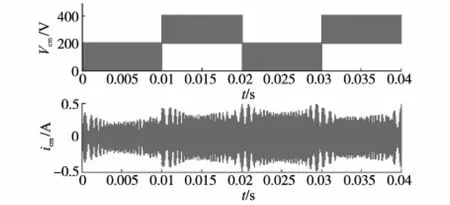
图7 单极性调制的全桥拓扑仿真波形Fig.7 Simulation waveforms of unipolar modulation full－bridge topology

3.2 双极性PWM调制

图2所示的单相全桥拓扑采用双极性PWM调制法控制时，在整个工作周期内，4个开关管均按开关频率的PWM调制。以电网电流正半周为例，当开关管S1，S4导通，开关管S2，S3关断时，

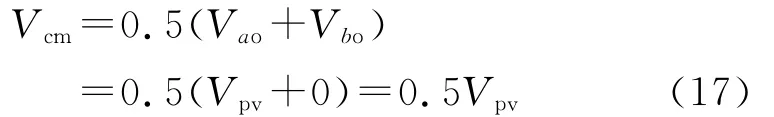
当开关管S1，S4关断，开关管S2，S3导通时，

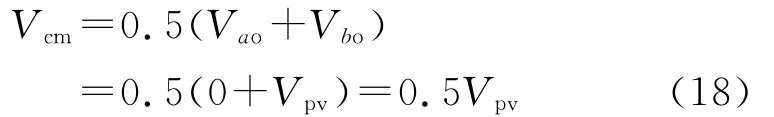
负半周开关管控制顺序与正半周相似。由式（17）、式（18）可知，在开关过程中，Vcm＝0.5Vpv，所以Vcm近似为定值，共模电流也近似为零。可见，采用双极性PWM调制法来控制单相全桥逆变器能够有效地抑制共模电流。图8为其共模电压Vcm和共模电流icm的波形。由图8可知，因共模电压Vcm基本为一定值，所以共模电流icm基本为零。因此，单相全桥拓扑结构的双极性调制法可有效地抑制共模电流。然而，从上述分析可知，在整个电网周期内4个开关管都以开关频率工作，这就会产生很大的开关损耗，从而限制了系统的效率。

图8 双极性调制的全桥拓扑仿真波形Fig.8 Simulation waveforms of bipolar modulation full－bridge topology

3.3 混合型PWM调制

图2所示的单相全桥拓扑采用混合型PWM调制法控制。在电网电流正半周内，开关管S1始终导通，S2，S3始终关断，S4按开关频率PWM调制；在电网电流负半周内，开关管S2始终导通，S1，S4始终关断，S3按开关频率PWM调制。以电网电流正半周为例，当开关管S1，S4导通，开关管S2，S3关断时，

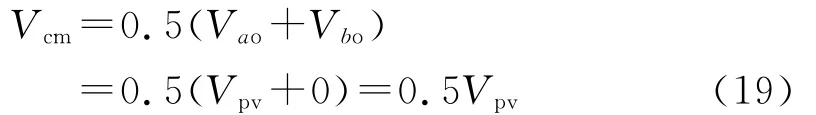
当开关管S1导通，开关管S2，S3，S4关断时，电流可通过开关管S1和开关管S3的反并联二极管进行续流。这时，

负半周分析过程与正半周相似。由式（19）、式（20）可知，在开关过程中，共模电压Vcm的幅值是变化的。因此，其共模电流很大，远远超过标准要求。图9为其共模电压Vcm和共模电流icm的波形。由图9可知，在开关过程中共模电压Vcm的幅值是在0，Vpv／2和Vpv之间变化的。因此共模电流的值很大。

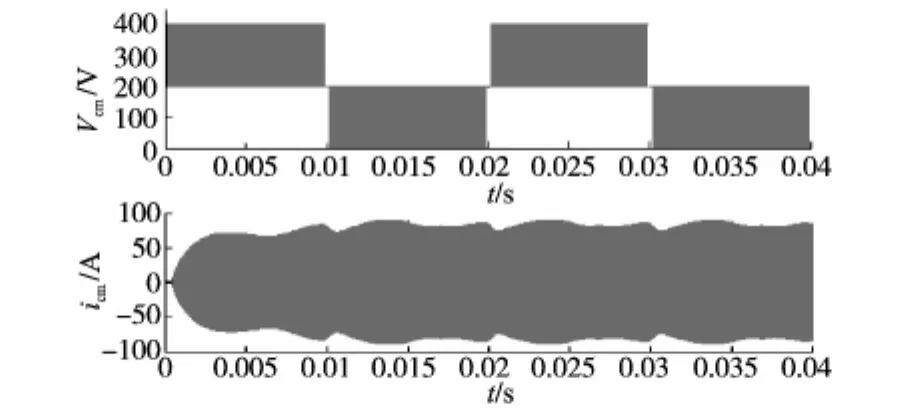
图9 混合型调制的全桥拓扑仿真波形Fig.9 Simulation waveforms of hybrid modulation full－bridge topology

表1给出了3种不同控制策略下的共模电压和共模电流的比较。

表1 不同控制策略的比较Tab.1 Comparison of different control strategies

由表1可知，双极性调制的全桥拓扑的共模电流（即漏电流）很小，而单极性和混合型调制的共模电流很大，因此采用双极性调制的控制策略可有效抑制漏电流，而采用另外2种控制策略不能抑制漏电流。但双极性调制法也存在明显的不足，在整个电网周期内，4个开关管均以开关频率工作，这就使得开关损耗是另外2种调制法的2倍，从而增加了系统的损耗，降低了系统效率。

为了解决全桥拓扑结构的不足，国内外一些学者通过提出新的拓扑结构来弥补全桥式拓扑的不足。如带直流旁路的拓扑结构、带交流旁路的拓扑结构、H5拓扑结构等。这些拓扑结构一般都采用单极性PWM调制控制策略，通过利用本身的结构特点，使主桥臂开关管关断时，续流开关管导通，从而使直流侧和交流侧断开，实现抑制漏电流的目的。

4 三相无变压器光伏并网逆变器系统的控制策略

对于图6所示的三相无变压器全桥式逆变器拓扑结构，分别采用传统SPWM控制方法［8］、空间矢量SVPWM和改进型SPWM控制方法，分析不同方法对抑制漏电流的影响。

4.1 理论分析

图10为3种不同控制方法的开关管调制图和共模电压图。由图10a可知，对于上桥臂开关管S1，S3，S5，当有2个导通时，共模电压Vcm＝2Vpv／3；当只有1个导通时，共模电压Vcm＝Vpv／3；当没有开关管导通时，共模电压Vcm＝0。因此，三相全桥拓扑结构采用传统的SPWM控制方法时，共模电压是在0～2Vpv／3之间变化的。所以根据前述抑制共模电流的一般规律可知，该控制方法不能抑制共模电流。由图10b可知，对于上桥臂开关管S1，S3，S5，当3个全导通时，共模电压Vcm＝Vpv；2个导通时，Vcm＝2Vpv／3；有1个导通时，Vcm＝Vpv／3；3个全关断时，Vcm＝0。因此，三相全桥拓扑结构采用空间矢量SVPWM控制方法时，共模电压是在0～Vpv之间变化的。所以根据前述抑制共模电流的一般规律可知，该控制方法也不能抑制共模电流。由图10c可知，当采用改进型SPWM控制方法时，上桥臂开关管S1，S3，S5在任何时刻都只有1个开关管导通，如S1导通，S3，S5关断时，则下桥臂开关管S2关断，S4，S6关断，因此共模电压为

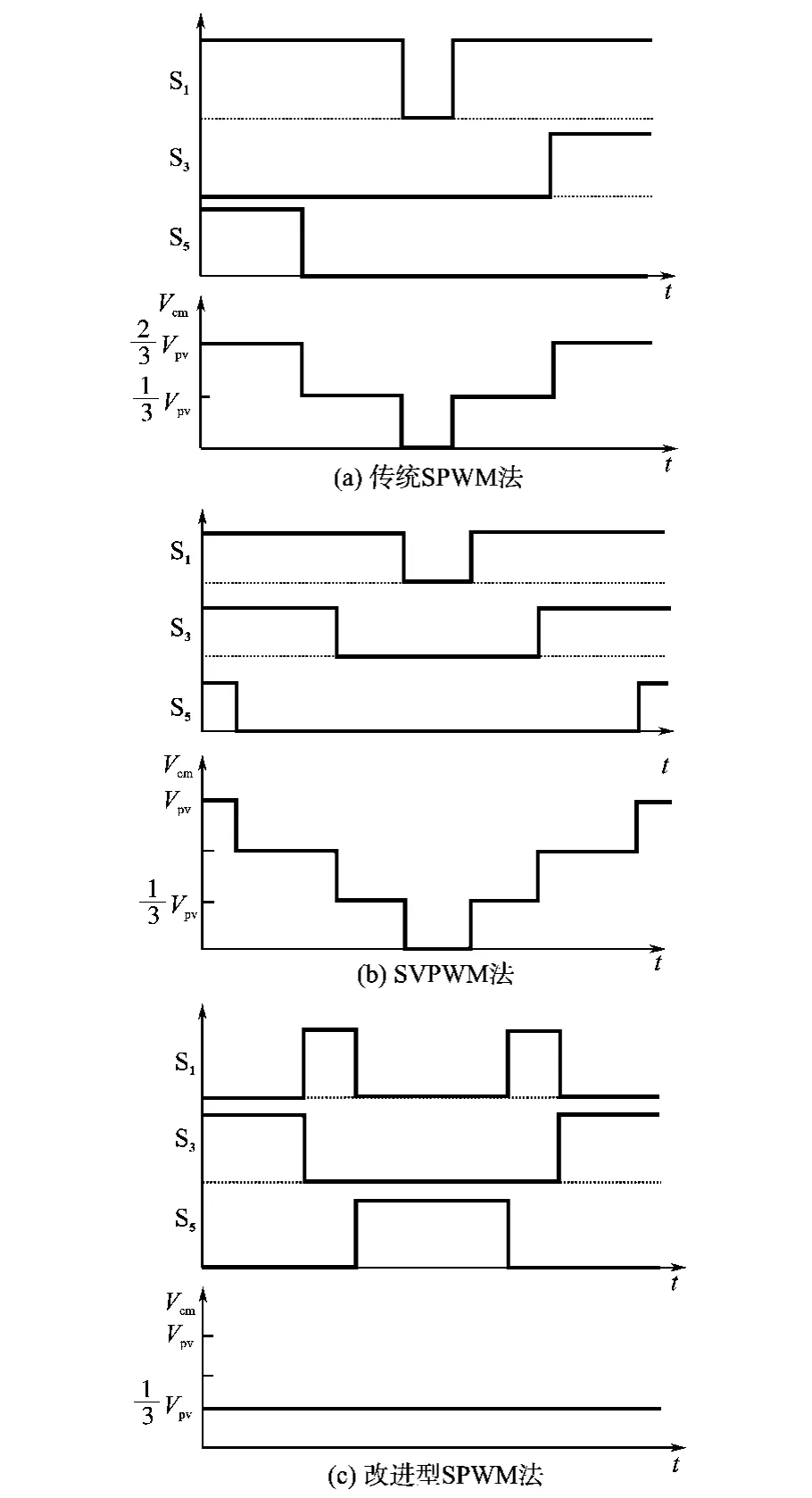
图10 不同方法的开关管调制图及共模电压Fig.10 The switch state and common－mode voltage of the different ways

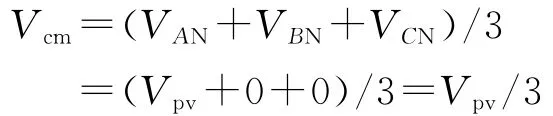
Vcm为一定值。开关管S3，S5导通时与S1分析一样。从以上分析可知该方法可有效地抑制共模电流。

4.2 仿真研究

对上述3种不同的调制法，分别对其进行仿真研究。仿真软件采用Matlab／Simulink。为了方便系统仿真，将PV阵列用直流电压源代替并且Vpv＝700V；输入直流端的电容C＝1mF，寄生电容Cp＝100nF。开关管频率fsw＝5kHz。输出滤波电感L＝2mH。电网频率fg＝50Hz，电网电压Vg＝220V（rms）。

图11为3种不同调制法的仿真结果。仿真波形均为共模电压Vcm和共模电流icm波形。由图11可知，传统SPWM法和SVPWM法因共模电压是变化的，故不能有效抑制共模电流（漏电流）。而本文提出的改进型SPWM法能使共模电压恒为Vpv／3，因此可有效抑制共模电流。

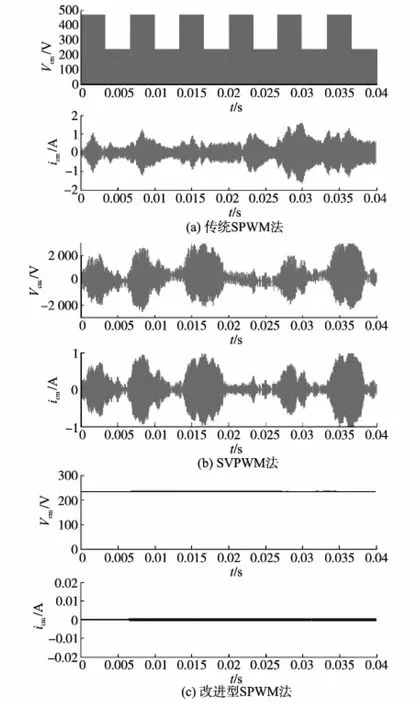
图11 不同调制法的仿真波形Fig.11 Simulation waveforms of the different modulation

5 结论

漏电流本质上就是共模电流，其产生的根本原因在于无变压器光伏并网逆变系统与地间的寄生电容Cp上共模电压变化率较大。因此要想有效抑制漏电流，就必须减小共模电压变化率。

对于双极性调制的单相全桥式逆变系统，虽能有效抑制漏电流，但因4个开关管在整个工作周期内均以开关频率调制而增加了开关损耗，影响了系统的效率。因此近年来国内外学者提出的新型单相拓扑均采用单极性调制法，充分利用新拓扑的结构特点，不但能有效抑制漏电流，还能减小开关损耗，提高系统效率，如直流旁路拓扑和交流旁路拓扑等。而三相全桥式拓扑，采用传统的SPWM法和SVPWM法是不能有效抑制漏电流的，而本文提出的改进型SPWM法因能够使共模电压恒定，故能有效抑制漏电流，从而为研究新型三相无变压器光伏并网系统的控制策略提供一些理论参考。

［1］Trends in Photovoltaic Applications：Survey Report of Selected IEA Countries Between 1992and 2008［R］.Report IEA－PVPS T1－18：2009.

［2］Roberto Gonzales，Jesus Lopez，Pablo Sanchis，et al.Transformerless Inverter for Single－phase Photovoltaic Systems［J］.IEEE Transactions on Power Electronics，2007，22（2）：693－697.

［3］Soeren B Kjaer，John K Pedersen，Frede Blaabjerg.A Review of Single－phase Grid－connected Inverters for Photovoltaic Modules［J］.IEEE Transactions on Industry Applications，2005，41（5）：1292－1302.

［4］Kerekes T，Teodorescu R，Borup U.Transformerless Photovoltaic Inverters Connected to the Grid，Applied Power Electronics Conference［C］∥APEC 2007－Twenty Second Annual IEEE，2007：1733－1737.

［5］Martina Calais，Vaddilios G Agelidis.Multilevel Converters for Single－phase Grid Connected Photovoltaic Systems－an Overview［J］.IEEE Transactions on Industry Applications，1998，1（10）：224－229.

［6］Roberto Gonzalez，Eugenio Gubia，Jesus Lopez，et al.Transformerless Single－phase Multilevel－based Photovoltaic Inverter［J］.IEEE Transactions on Industrial Elebctronics，2008，55（7）：2694－2702.

［7］Araneo R，Lammens S，Grossi M，et al.MEC Issues in Highpower Grid－connected Photovoltaic Plants［J］.IEEE Trans.Electromagnetic Compatibility，2009，51（3）：639－648.

［8］Kerekes T，Klumpner R，Summer M，et al.Evaluation of Three－phase Transformerless Photovoltaic Inverter Topologies［J］.IEEE Transactions on Power Electronics，2008，57（4）：1360－1367.