永磁同步电机效率改善策略比较研究

邢绍邦，罗印升，宋伟，陈太洪

（1.江苏技术师范学院 电气信息工程学院，江苏 常州 213001；2.南京航空航天大学 自动化学院，江苏 南京 210016）

1 引言

永磁同步电动机体积小、效率高、功率密度大，由其组成的闭环调速系统能够实现高精度、高动态性能、大范围的速度和位置控制，在要求高性能、快速响应的场合具有很好的应用前景［1－2］。为了改善永磁同步电动机调速系统的控制性能，不少学者将先进控制理论应用于其中并取得了很好的控制效果。另一方面，能源短缺促使人们在改善调速特性的同时提升电机运行效率。对此人们也进行了大量的工作，文献［3］提出了基于在线搜索技术的最小功率控制策略，该方法无需电机的精确模型，通过在线搜索的方式使输入功率达到最小，实现效率优化；文献［4－6］提出了基于损耗模型的控制策略，该方法通过实时检测或估计电机的转速和电流信号，依据电机的动态损耗模型，推导出损耗最小或效率最高时的最优磁通值。文献［7－8］提出了最大转矩电流比控制方式，该方法分析了输出转矩一定时所需的最小定子电流，具有响应速度快，容易实现等优点。

最小功率控制策略虽然具有对参数变化反应迟钝和适应性强的优点，但其寻优时间过长，节能效果并不能令人满意。在负载变化快的场合，反而可能使控制性能下降。因此，本文基于永磁同步电机（PMSM）直接转矩控制（DTC）平台，针对最小损耗模型和最大转矩电流比两种效率改善策略进行了详细的比较研究。通过计算PMSM的铜损和铁损，建立了最小损耗模型。利用最优化理论分析了最大转矩电流比情况下转矩与最小定子电流之间的关系，采用曲线拟合的方法给出了确切的最优励磁电流表达式。最后对仿真实验结果进行了详细的比较分析。

2 永磁同步电机效率改善策略

电机运行时，不同的定子磁链能够提供的最大输出转矩不同。为得到快速的系统动态响应，传统的直接转矩控制系统选择较大的定子磁链给定值，并且在系统整个运行期间维持不变。这样必然导致系统在空载或轻载运行时励磁电流过大，造成过多的励磁损耗，系统效率降低。为提高系统的运行效率，必须对定子磁链给定进行有效的控制。由式及α－β到d－q 坐标变换，可知定子磁链给定值为

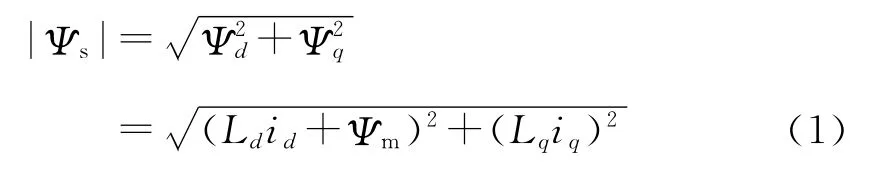
其中，Ψm为转子永磁体的磁链值，Ld，Lq为定子dq轴电感，皆为常数。故问题转化为求给定转矩下的最优励磁电流问题。

2.1 基于最小损耗模型的效率改善

该方法通过分析永磁同步电机的最小损耗模型，求得最优定子电流动态表达式。在系统运行时根据不同工况实时地求出最优励磁电流，进而实时计算出最优磁链给定值。

众所周知，永磁同步电机的损耗包括机械损耗、铜损和铁损等。其中机械损耗随转速及工况的不同而不断变化，是不可控的。此处仅考虑可控部分的电气损耗，包括铁损和铜损。图1、图2分别表示了两相同步旋转坐标系（dq）下永磁同步电机等效电路［2，5－6］。

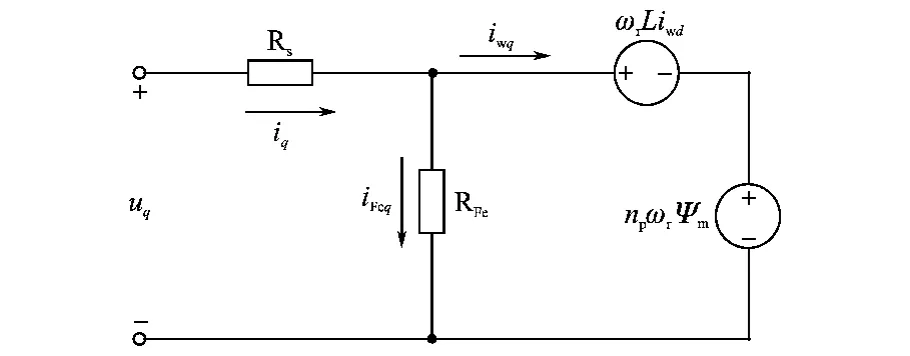
图1 永磁同步电机q轴动态等效电路Fig.1 PMSMqaxis dynamic equivalent circuit

图2 永磁同步电机d轴动态等效电路Fig.2 PMSMdaxis dynamic equivalent circuit

图1、图2中，u，i分别为定子电压与电流矢量；iw，iFe分别为有功与铁损电流矢量（图中下标d，q表示相应分量）；R与L为定子电阻与电感；Ψm为转子永磁体的磁链值；ωr为轴机械转速；np为极对数；RFe为等价的回路铁损电阻。

对应的稳态方程为

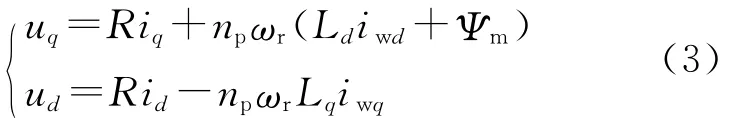
又因为

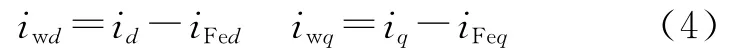
则得到

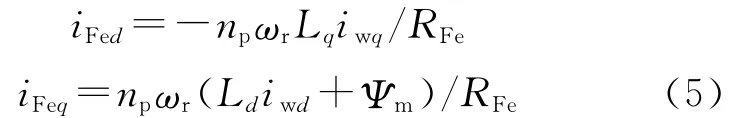
则永磁同步电机的铜损为

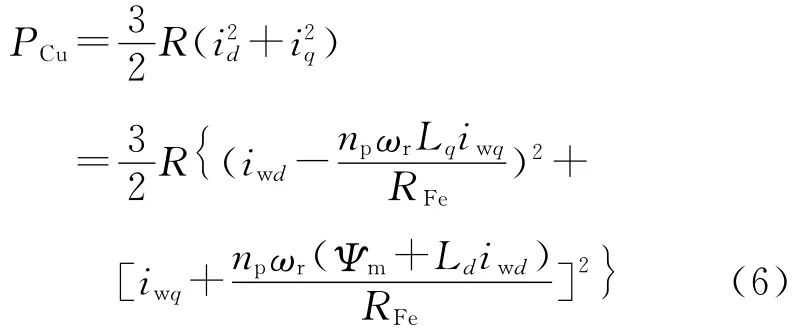
铁损为

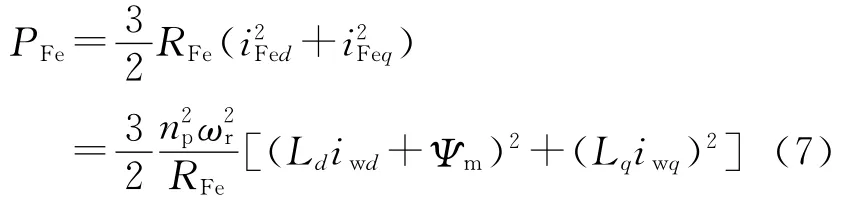
则总的电气损耗为

式（8）显示总的电气损耗仅与有功电流iwd有关（当电机到达稳态，即ωr与Te为常值时）。令dPloss／diwd＝0，求得损耗最小值时的最优电流iwd·opt为

柏拉图在第一阶段的文本中明确提到了无蔽者。可是，洞穴中的被缚者果真把阴影当成无蔽者了吗？严格说来，被缚者并非把阴影当成了无蔽者，而是把他们在面前墙壁上看到的“东西”当做“无蔽者”来谈论。他们既然看不见背后的火光和墙头的人造物，就不会看到面前的“阴影”。在第一阶段，被缚者们径直谈论无蔽者，对他们来说，还不存在无蔽者与被遮蔽者的区分。[8]133

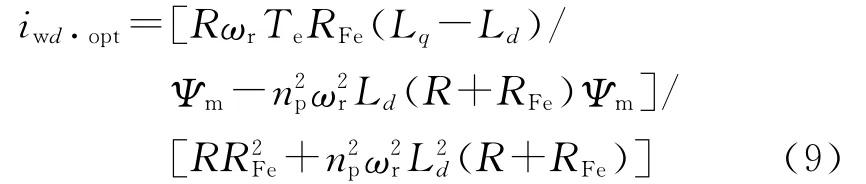
系统运行过程中根据系统转速和转矩信息实时求得最优励磁电流iwd·opt，进而根据式（1）计算出最优磁链给定值，便可以保证系统始终运行在总的电气损耗最小点，从而提高了电机的运行效率。

2.2 基于最大转矩电流比的效率改善

采用最大转矩电流比（MTPA）控制方法，即使得电机在输出相同的电磁转矩下电机定子电流最小，问题等效于以下的极值问题：

为求解式（10），做Lagrange辅助函数如下：

式中：λ为Lagrange乘子。

将式（11）分别对id，iq和λ求偏导数并令其为零，得到

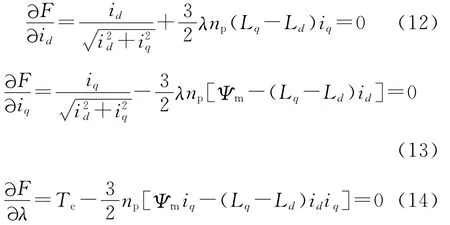
由式（13）、式（14）两式可求出id和iq之间的关系为：

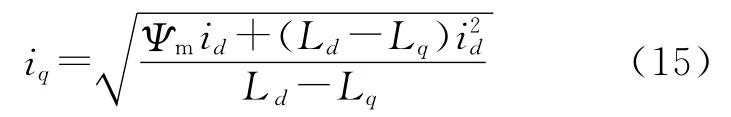
将式（15）代入式（14），便可求出Te与id之间的关系：

式（15）、式（16）即为MTPA运行时最优定子电流id，iq与转矩Te之间应满足的关系式。

在具体控制中需要根据参考转矩求解MTPA运行时的参考电流，但是由式（16）可知，要反解出id＝f（Te）的关系式是非常困难的，此处采用曲线拟合的方法进行近似求解。

首先在 Matlab中按照式（16）画出id＝f（Te）的函数曲线，此时Matlab是按照最优的近似数值解求解的，然后根据式（15）再得到iq＝f（Te）的函数曲线。如图3中的实线所示。接下来利用Matlab曲线拟和工具箱cftool用多项式函数拟合id，iq曲线，其中多项式的阶数可以方便地人为选择，针对仿真的电机参数，本文选用3阶多项式函数，其具体的表达式如下：

拟合效果如图3中的虚线所示。

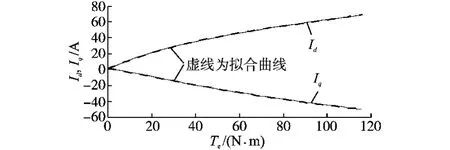
图3 电流id，iq与转矩关系曲线Fig.3 Curves of relations between currents id，iqand torque

当参考转矩给定后，根据式（17）求出MTPA运行时的最优参考电流id，iq，再由式（1）便可求得定子磁链给定值，以达到效率改善的目的。

3 试验结果分析

为了验证本文提出的效率改善策略的有效性，构建基于最小损耗模型和MTPA效率改善策略的永磁同步电机直接转矩控制系统Matlab／Simulink仿真模型分别如图4和图5所示。

图4 基于最小损耗模型的效率改善系统仿真模型Fig.4 Simulation model of efficiency improvement system based on minimum loss model

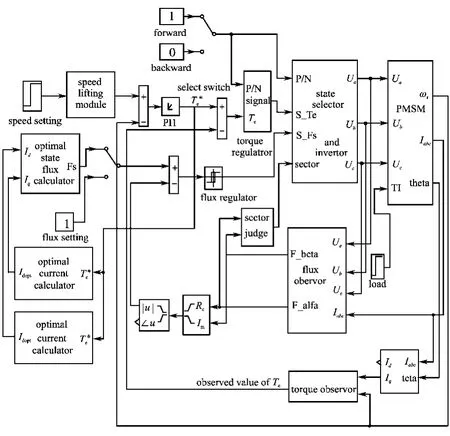
图5 基于MTPA的效率改善系统仿真模型Fig.5 Simulation model of efficiency improvement system based on MTPA

实验过程中永磁同步电机的参数如下：额定功率Pe＝8kW，额定电压U＝380V，额定转速ωr＝1500r·min－1，额定转矩Te＝5N·m，永磁体磁链Ψm＝0.175Wb，极对数np＝3，d轴电感Ld＝0.0045H，定子电阻R＝2.875Ω，q轴电感Lq＝0.0085H，转动惯量J＝0.0008kg·m2。

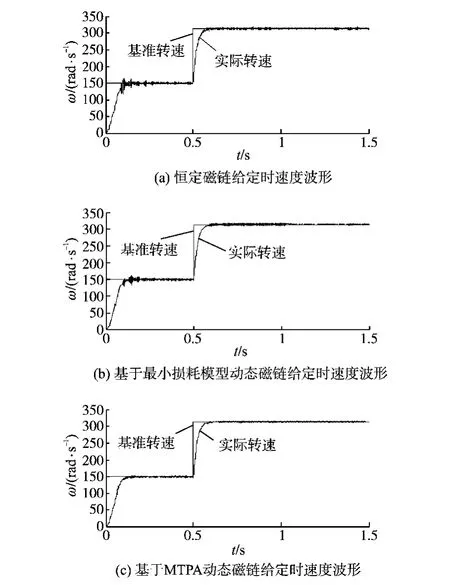
图6 不同磁链给定方式下的速度波形Fig.6 Speed waveforms in different flux given ways

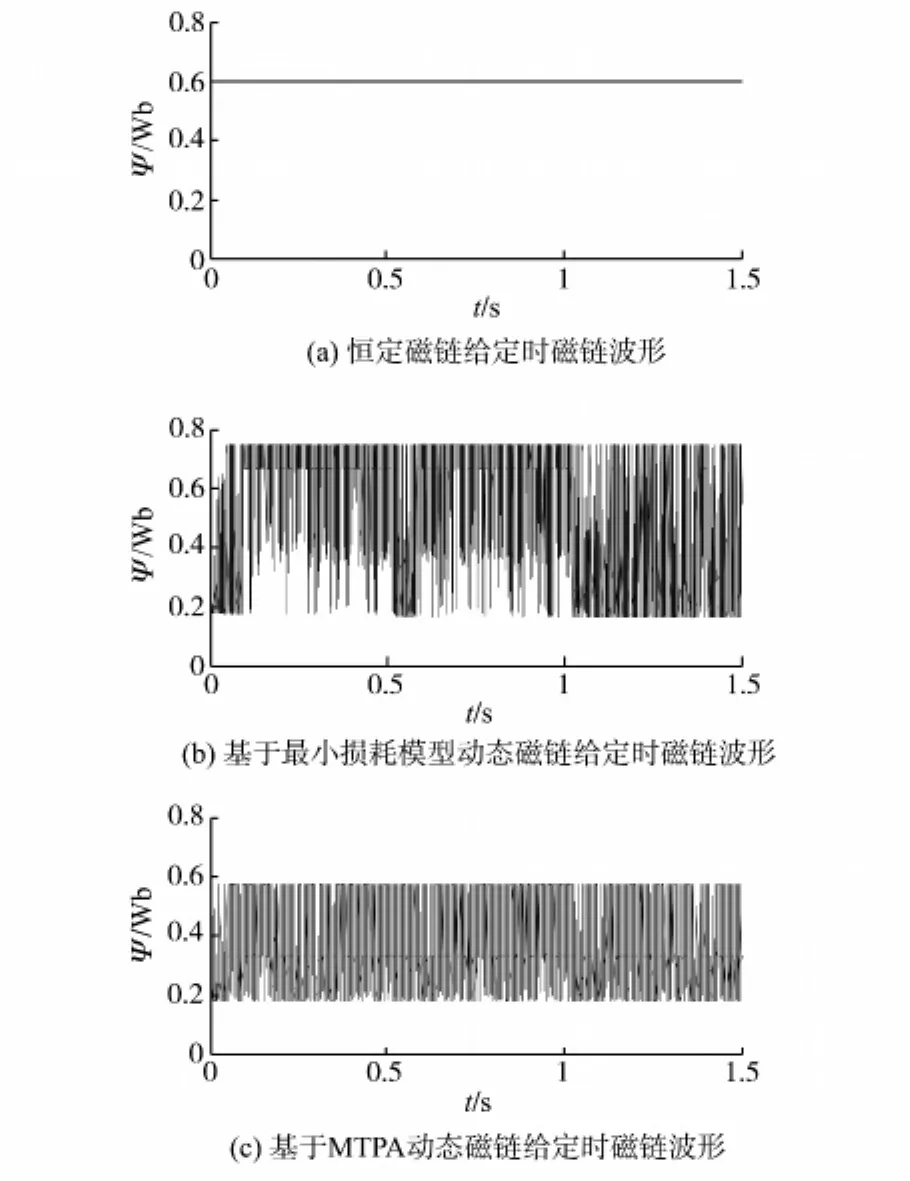
图7 不同磁链给定方式下的磁链波形Fig.7 Flux waveforms in different flux given ways

图6～图8分别为不同的磁链给定方式下的永磁同步电机直接转矩控制系统的速度、磁链和定子电流波形。初始转速设置为150rad／s，空载启动，在0.5s时变为314rad／s。在1s时突加负载至5N·m。

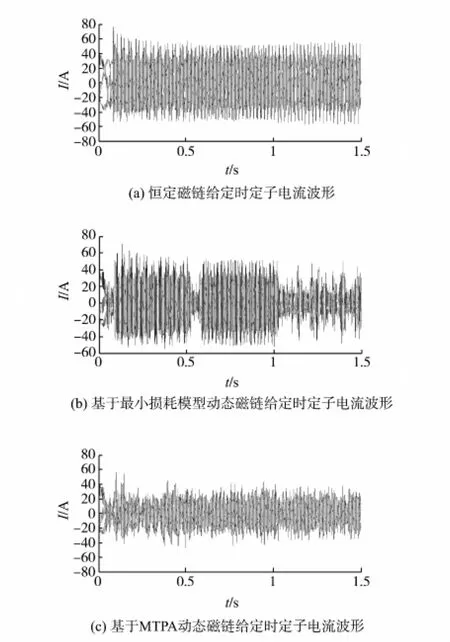
图8 不同磁链给定方式下的定子电流波形Fig.8 Current waveforms in different flux given ways

通过图6可以看出，3种磁链给定方式下的直接转矩控制均可以较好地跟踪给定转速，但基于MTPA动态磁链给定方式和基于最小损耗模型动态磁链给定方式时，速度波形要明显优于恒定磁链给定方式下的速度响应波形，其中基于MTPA动态磁链给定方式效果最好。

从图7可以看出，基于MTPA动态磁链给定和基于最小损耗模型动态磁链给定的直接转矩控制系统的磁链与常规的直接转矩控制系统的磁链有明显的区别，它随着系统的需要而动态变化。

从图8可以看出，在相同的输出转矩时，基于MTPA动态磁链给定方式和基于最小损耗模型动态磁链给定方式能够明显地减小定子电流。其中，采用基于MTPA动态磁链给定的直接转矩控制方式得到的定子电流要明显小于其他两种磁链给定方式，可见采用基于MTPA动态磁链给定方式可以有效提高系统的运行效率，特别是低负载情况下，提升效果较为明显。

综合上述仿真结果可以看出，基于MTPA动态磁链给定方式和基于最小损耗模型动态磁链给定方式都能够显著提高电机的运行效率，其中基于MTPA动态磁链给定方式的效果更为明显。

4 结论

在分析主要的永磁同步电机效率改善策略的基础上，本文基于永磁同步电机（PMSM）直接转矩控制（DTC）平台，针对最小损耗模型和最大转矩电流比两种效率改善策略进行了详细的比较研究。建立了PMSM的最小损耗模型并利用其求出了最优励磁电流的实时表达式。利用最优化理论分析了最大转矩电流比情况下转矩与最小定子电流之间的关系，采用曲线拟合的方法给出了确切的最优励磁电流表达式。最后通过仿真实验验证了本文所提方案的合理性，并对结果进行了详细的比较分析。仿真试验表明，基于MTPA动态磁链给定方式和基于最小损耗模型动态磁链给定方式都能够显著提高电机运行效率，其中以MTPA动态磁链给定方式效果更为明显。

［1］Bimal K.bose.Modern Power Electric and AC Drives［M］.Englewood Cliffs：Prentice Hall，2002.

［2］李永东.交流电机数字控制系统［M］.北京：机械工业出版社，2003.

［3］刘小虎，谢顺依，郑立捷.一种改进的感应电机最大效率控制技术研究［J］.中国电机工程学报，2005，25（6）：95－98.

［4］Calogero Cavallaro，Antonino Oscar Di Tommaso，Rosario Miceli.Efficiency Enhancement of Permanent Magnet Synchronous Motor Drives by Online Loss Minimization Approaches［J］.IEEE Trans.on Industrial Electronics，2005，52（4）：1153－1160.

［5］崔培良，赵克友.面装永磁同步电机最小损耗的速度控制［J］.电机与控制应用，2006，33（11）：35－38.

［6］王晓磊，赵克友.永磁同步电机最小损耗的直接转矩控制［J］.电机与控制学报，2007，11（4）：331－334.

［7］郎宝华，刘卫国，贺虎成，等.基于最大转矩电流比动态磁链给定的直接转矩控制［J］.电气传动，2008，38（1）：23－26.

［8］许峻峰，徐英雷，冯江华，等.永磁同步电机直接转矩控制中定子磁链的分析［J］.电气传动，2005，35（1）：10－12.