地下水封洞库围岩块体失稳矢量分析方法研究

谢良甫，晏鄂川，季惠彬

(中国地质大学(武汉)工程学院，武汉 430074)

近年来，针对地下洞室围岩块体失稳的评价方法研究，国内外学者主要将围岩块体看作弹塑性材料，考虑结构的不连续性和本构方程的非线性，根据边界条件作出适当的假设，即针对非连续岩体力学开展了基础研究，如1969 年 D.H.Trollope［1］分析了非连续体的静力平衡问题;1971年 P.A.Cundall［2］提出离散元数值计算法;1977年，我国学者石根华提出了赤平投影图上判断滑落体的方法，进而采用矢量代数法分析岩体稳定性［3－4］，并在此基础上于1985 年与 R.E.Goodman 合作创立了块体理论［5］。

块体理论自创立以来，得到了国际岩石力学界的普遍赞誉和应用。1988年，刘锦华［6］系统全面地将块体理论介绍到国内，使块体理论在国内得到迅速发展和应用，该理论目前已成为边坡和地下工程岩体稳定分析的一种有效方法［7－10］。块体理论主要分析手段有矢量分析法、极射赤平投影分析法和后期张子新创立的赤平解析法，赤平投影需要一一作图，且对作图要求精确度高;赤平解析法应用不够广泛。基于此，本文将采用矢量分析方法分析某地下水封洞库围岩块体稳定性，使洞库在开挖前能采取相应防治措施，达到提前预报的目的;并研究矢量法评价地下水封洞库围岩块体稳定性。

1 工程概况及地质背景

拟建地下水封洞库设计库容500×104m3，共布设10条主洞室，每2个主洞室之间通过4条支洞相连组成一个洞罐，共分为5个洞罐组。主洞室设计长度为923 m，设计洞跨20 m，洞高30 m，截面形状为直墙圆拱形，洞室轴线走向为NE10°。

根据地质调查综合分析，片麻状花岗岩是拟建洞库的主要岩体，片麻理产状一般为 NE90°～105°∠38°～50°，库区内主要发育一组缓倾角节理及3组陡倾角节理(表1)。

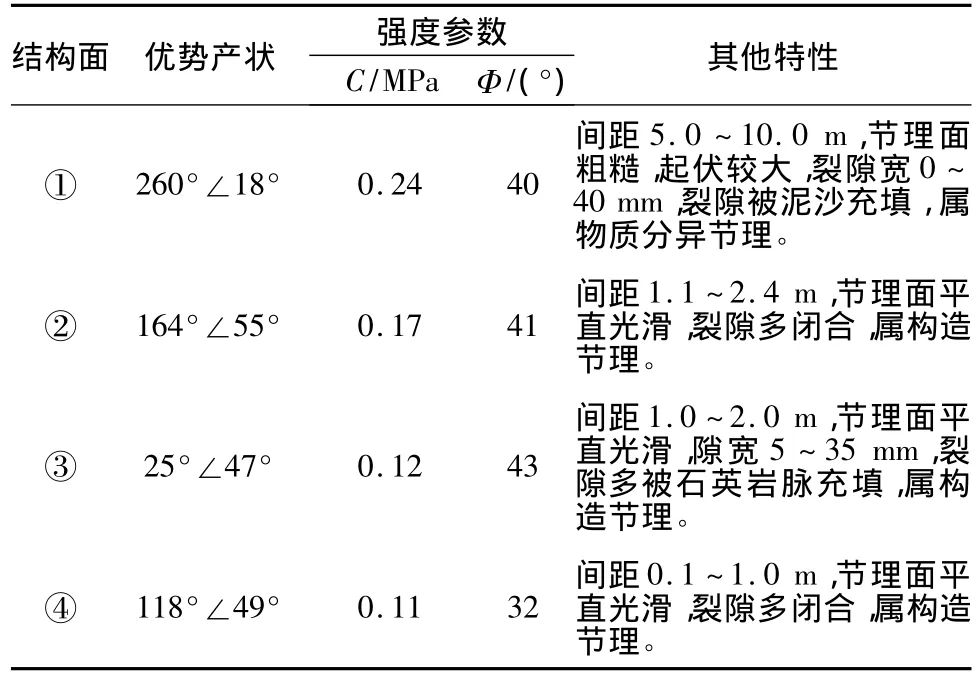
表1 结构面主要力学参数及特性Table 1 Main mechanical parameters and properties of structural planes

2 围岩块体矢量法分析

2.1 关键块体判别原理

(1)根据块体理论，判别关键块体首先应找出

式中:JP为裂隙锥，表示仅以结构面为界的岩体半空间所构成的棱锥;EP为开挖锥，表示仅以临空面为界的岩体半空间所构成的棱锥;BP为块体锥，表示由一个以上临空面和若干组结构面为界的岩体半空间所组成的棱锥。

式(1)在矢量分析法中的意义为:若一块体可动，则其由结构面和临空面共同构成的块体有限(EP∩JP=Ø)，而仅由结构面构成的裂隙块体为无限(JP≠Ø)。

因此首先找出已知结构面条件下的所有非空裂隙锥;然后从这些非空裂隙锥与临空面的组合关系中确定所有可动块体。

(2)在判别出可动块体后，需要进一步对其可能的失稳形式进行分析，裂隙锥可以用符号编号JP［I(a1)，I(a2)，…，I(an)］(块体编号规则按文献［6］)，因此只要求出相应某种运动形式的各结构面向内单位法线矢量^νi，就可以确定相应运动形式的JP编号。块体失稳形式共分为脱离岩体运动、单面滑、双面滑3种，分别求出3种不同运动形式的运动学条件，进而确定相应运动形式的块体编号。

(3)在找出可动块体后，还应找出在自重条件下首先失稳滑动的块体(即关键块体)。关键块体的判别是通过力学分析从可动块体中找出的，力学分析的主要内容是依据作用于可动块体上的力的平衡方程计算在不同运动形式下块体的剩余下滑力(F)。当其剩余下滑力大于零时，该块体为关键块体。

2.2 工程实例分析

2.2.1 判别非空裂隙锥

(1)通过表1四组结构面产状(倾角αi，倾向βi)计算出相应向上单位法线矢量:

(2)求出各界面的交线，即棱矢量:

(3)求出方向参量:可动性块体，可动块体应满足如下条件:

将由式(4)计算出的方向参量组成一个方向参量矩阵为

再建立各块体编号矩阵(块体编号规则按文献［6］)，如块体 1101，其矩阵编号为

(4)建立判别矩阵［T］

建立无限裂隙块体的判别矩阵:

在判别矩阵［T］中，若相应Iij的某行数字皆为0或同时含有－1，+1，则Iij不是其真实棱;若皆为0和+1，则 Iij为其真实棱;若皆为0和 －1，则 －Iij为其真实棱。

通过上述分析可得出，由此4组结构面产生的无限裂隙块体共 14 个:0000，0001，0010，0011，0100，0101，0111，1000，1010，1011，1100，1101，1110，1111。

2.2.2 确定可动块体

基于非空裂隙锥的判别，考虑与各临空面组合关系，对上述14个无限裂隙块体按照相同步骤建立其可动性判别矩阵:

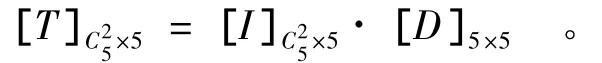
通过分析得出，顶面可动块体:1011，1110，1111;东边墙可动块体:0001，0011，0111;西边墙可动块体:1000，1100，1110;南边墙可动块体:0100，1100，1101;北边墙可动块体:0010，0011，1011。

2.2.3 关键块体判别

在判别关键块体前，首先应确定各可动块体的失稳形式，然后计算其剩余下滑值。

2.2.3.1 块体运动形式判断

当块体脱离岩体运动时:

式中:^s为运动方向矢量;^r为主动力合力;^νl为结构面向内单位法线矢量;l为块体各结构面。

当块体沿单结构面i运动时:

当块体沿双结构面i，j运动时:

通过上述计算可得出相应各运动形式的块体编号(表2)。表2中r表示直接掉落，si表示沿界面i滑动，sij表示沿界面 i，j滑动。

表2 相应各运动形式的块体编号Table 2 Block numbers of each corresponding motion form

2.2.3.2 剩余下滑力计算

判别出可动块体及其失稳形式后，还应找出在自重条件下首先失稳滑动的块体(即关键块体)。关键块体的判别是通过力学分析从可动块体中找出的，力学分析的主要内容是依据作用于可动块体上的力的平衡方程计算在不同运动形式下块体的剩余下滑力(F)。当其剩余下滑力大于零时，该块体为关键块体。

在仅有重力作用下，不同运动形式下的剩余下滑力公式如下:

(1)直接掉块

F=|r→|，即 F 等于块体自重;

(2)沿单面i滑动

(3)沿双面 i，j滑动

在此剩余下滑力的计算中只考虑结构面的摩擦系数，使其结果偏于安全，以免发生关键块体的漏判，并且取r=(0，0，－1)，这样计算的F为无量纲值。

通过计算，分别得出各可动块体的剩余下滑力，并可判别出各临空面关键块体(表3)。

表3 各临空面关键块体分布情况Table 3 Distribution of key blocks in each free face

由表3可看出，在自重作用条件下，洞室顶部关键块体最多，西边、北边墙次之，且关键块体主要以结构面②、④单面滑动。由于洞室几何形状为沿近南北向呈长条状，因此西边墙长度远长于北边墙，故洞室顶部和西边墙将是关键块体出现的主要临空面，应重点防治。

3 结论

(1)在拟建地下水封洞库中，洞室顶部的关键块体所占比例最大，且优势明显;西边墙与北边墙稳定性较差，南边墙次之，东边墙稳定性最好。应重点防治洞室顶部和西边墙关键块体失稳。

(2)根据关键块体剩余下滑力值，可以对实际工程施工中存在的关键块体采取有针对性的防治措施。

(3)关键块体主要以结构面②、④单面滑动，占总数的80%，因此在洞库开挖施工时，针对这2个结构面的出露处要加强监测。

(4)矢量法适用于评价地下水封洞库围岩块体稳定性，能准确地分析出各开挖面关键块体;但矢量法无法准确确定关键块体的失稳具体部位，以及对曲面洞壁块体稳定性分析均有待进一步的改进与研究。

［1］STAGG R G.Rock Mechanics in Engineering Practice［M］.New York:John Wiley＆ Sons，1969.

［2］CUNDALL P A.A Computer Model for Simulating Progressive Large-scale Movements in Block Rock Systems［C］∥Proceedings of the International Symposium.On Rock Fracture(ISRM).Nancy，France，4 －6th October，1971.

［3］石根华.岩体稳定分析的赤平投影方法［J］.中国科学，1977，(3):269 －271.(SHI Gen-hua.Stereographic Projection Method of Stability Analysis of Rock Mass［J］.Science in China(Series A)，1977，(3):269 －271.(in Chinese))

［4］石根华.岩体稳定分析的几何方法［J］.中国科学，1981，(4):487 －495.(SHI Gen-hua.Geometric Method of Stability Analysis of Rockmass［J］.Science in China(Series A)，1981，(4):487 －495.(in Chinese))

［5］GOODMAN R E，SHI G H.Block Theory and Its Applications to Rock Engineering［M］.Englewood Cliffs:Prentice-hall，1985.

［6］刘锦华，吕祖珩.块体理论在工程岩体稳定分析中的应用［M］.北京:水利水电出版社，1988.(LIU Jinhua，LU Zu-heng.Block Theory and Its Application to Rock Engineering［M］.Beijing:China Water Power Press，1988.(in Chinese))

［7］张子新，孙 钧.块体理论赤平解析法及其在硐室稳定分析中的应用［J］.岩石力学与工程学报，2002，21(12):1756 －1760.(ZHANG Zi-xin，SUN Jun.Stereoanalytic Method for Block Theory and Its Application in Stability Analysis of a Cave［J］.Chinese Journal of Rock Mechanics and Engineering，2002，21(12):1756 －1760.(in Chinese))

［8］张奇华，邬爱清，石根华.关键块体理论在百色水利枢纽地下厂房岩体稳定性分析中的应用［J］.岩石力学与工程学报，2004，23(15):2609－2614.(ZHANG Qi-hua，WU Ai-qing，SHI Gen-hua.Application of Key Block Theory to Analysis of Rock Stability for Underground Plant in Baise Hydraulic Project［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23(15):2609 －2614.(in Chinese))

［9］梁 宁，伍法权，刘 彤，等.块体理论赤平解析法在锦屏二级水电站皮带机隧道稳定分析中的应用［J］.工程地质学报，2009，17(3):383－388.(LIANG Ning，WU Fa-quan，LIU Tong，et al.Application of Block Theory Based Stereo-analytical Method to Stability Analysis of Conveyor Tunnel at Jinping II Hydropower Station［J］.Journal of Engineering Geology，2009，17(3):383－388.(in Chinese))

［10］张子新，廖一蕾.基于块体理论赤平解析法的地下水封油库围岩稳定性分析［J］.岩石力学与工程学报，2010，29(7):1339 －1347.(ZHANG Zi-xin，LIAO Yilei.Stability Analysis of Surrounding Rock Mass of Water-tight Oil Storage Using Block Theory Based on Stereoanalytical Method［J］.Chinese Journal of Rock Mechanics and Engineering，2010，29(7):1339 － 1347.(in Chinese ))