基于多尺度相关和机理建模的炉膛压力分析

田 亮， 刘鑫屏， 王 琪， 刘吉臻

（1.华北电力大学 新能源电力系统国家重点实验室，北京102206；2.内蒙古电力科学研究院，呼和浩特010020）

热力系统状态信号之间的相互影响关系非常复杂，对其直接进行机理分析存在一定的困难［1］.目前数据采集和记录已相对比较容易，利用数据分析方法对过程中的历史数据进行预处理，发现信号的一些变化规律及信号间的影响关系，在此基础上再进行针对性的机理分析往往能够明显降低研究难度［2］.

相关分析是一种应用非常广泛的数据处理方法，但传统相关系数或相关函数只能够描述时域内信号在整体上的相关性.在一个信号同时受多个信号影响或有明显噪声干扰存在的情况下，直接应用此类方法不能取得很好的效果［3－4］.小波分析能够获得不同时间尺度和频率尺度下信号的特征，但最大问题是算法比较复杂，难以实现大规模的实时挖掘.

火力发电厂监控信息系统（SIS）保存机组全部运行数据，一台典型600MW机组的记录数据超过15 000个，大规模数据挖掘需要一种简单有效的方法.借鉴小波分析思想，设计一种简单的多频率尺度相关分析方法，发现不同频率尺度下信号间相互影响相互作用的规律，同时算法简单并且具有明确的物理意义，适合于大规模工程的应用［4］.

火电机组中的锅炉炉膛压力是机组安全性监控的主要参数.受到各种因素的影响，炉膛压力变化剧烈，同时炉膛压力信号也影响许多其他运行参数［5］.机组集控运行规程以及现场经验表明，与锅炉燃烧相关的绝大部分故障都会导致炉膛压力发生异常波动，同时也有通过炉膛压力频谱特性来分析判断燃烧稳定性的研究［6－9］.然而，对炉膛压力与燃烧状态之间的内在联系有必要进行深入的研究分析.

1 多频率尺度相关分析

1.1 滤波器设计

根据小波分析的思想，在频域内推导通过多尺度滤波器将信号分解的方法.信号x0（s）可分解为

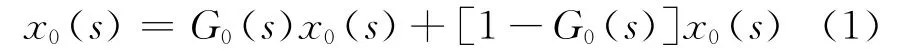
令xh1（s）＝［1－G0（s）］x0（s），x1（s）＝G0（s）×x0（s），对x1（s）继续进行分解得

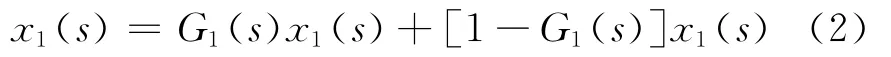
令xh2（s）＝［1－G1（s）］x1（s），x2（s）＝G1（s）×x1（s），可以对x2（s）继续分解.

同理，令xh（n＋1）（s）＝［1－Gn（s）］xn（s），xn＋1（s）＝Gn（s）xn（s），则

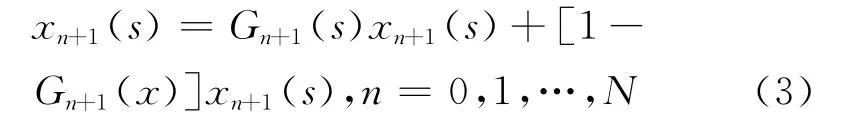
依次类推，可将xn（s）不断分解，最终可得

在式（1）～式（4）中，选择不同的Gn（s），可构造成不同的滤波器组，对信号x0（s）进行不同性质的分解，但要求Gn（s）具有稳定的极点.例如

式中：k为步距系数，k＞1；T0为基本滤波时间；m为滤波阶次，取正整数.

这样Gn（s）为一个低通滤波器.k越大，滤波器频率尺度的步距越大；T0越大，基本滤波时间越大，基本截止频率越低；m越大，滤波器组阶次越高，其特性越接近理想滤波器的特性.信号分解的过程为首先将一个信号分解为低频部分和高频部分，然后再对其低频部分进一步分解为相对高频部分和相对低频部分，如此反复n次，实际上构成了1个高通、n个带通、1个低通滤波器组.

与小波分析类似，通过选择合适的Gn（s）可以得到不同频率尺度、不同时间尺度下信号的变化特征，并且这样的分解过程具有可逆性.当然，滤波器组选择是否合适会影响分析结果.

1.2 线性相关分析

在特定时间段，时域内信号x（t）和信号y（t）的相关函数定义见式（6）.为了有效消除各种噪声的影响，分析时间 T 应足够长［10－11］.

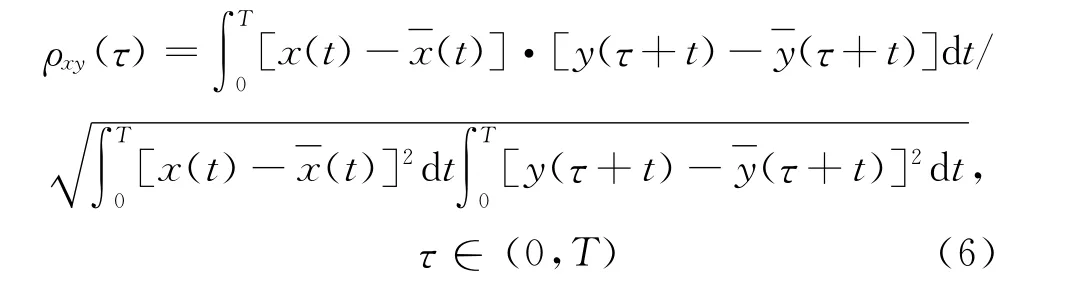
应用时，首先对2个预分析信号x（t）和y（t）进行多尺度滤波处理，分别得到一系列信号在不同频率尺 度 下 的 分 量：xh1（t）、xh2（t）、…、xh（n＋1）（t）、xn＋1（t）和yh1（t）、yh2（t）、…、yh（n＋1）（t）、yn＋1（t）.然后分别求解各信号分量之间的相关函数，如xh1（t）分别与yh1（t）、yh2（t）、yn＋1（t）的相关函数和xh2（t）分别与yh1（t）、yh2（t）、yn＋1（t）的相关函数等，得到相关函数最大值矩阵ρXY和相关函数最大值出现的时间矩阵τXY.相关函数的最大值较大，则相关性较好.ρXY和τXY分别为

1.3 特征描述

与传统相关分析相比，多频率尺度相关分析方法能够较为细致地描述一个信号同时受多个信号影响时的情况，并且通过分析相关函数的最大值及其出现时间，可以初步判断信号之间的影响关系及特征.信号x（t）和信号y（t）之间的典型特性为：

（1）低通特性.x（t）中、低频分量与y（t）高、中频分量间的相关性好.

（2）高通特性.x（t）高、中频分量与y（t）低、中频分量间的相关性好.

（3）纯迟延特性.x（t）与y（t）高、中、低对应频率分量的相关性均较好，且相关函数最大值出现的时间比较一致.

2 应用实例

采用此方法对某600MW机组的运行数据进行分析.根据式（1）～式（5），选择T0＝10，k＝5，m＝2，n＝0、1，构成2个不同截止频率的低通滤波器，将信号分解为低频分量、中频分量、高频分量，并进行多尺度频率特性分析.图1～图4表示各种影响因素中与炉膛压力相关性较好的锅炉燃料量、总送风量和引风量信号的高频、中频和低频频率分量，而其他影响因素与炉膛压力之间的相关性都非常小.

由图1～图3可以发现，炉膛压力低频分量、中频分量与锅炉燃料量和送风量的中频分量和高频分量之间存在较好的相关性，相关函数最大值分别为0.86、0.81和0.82、0.81.根据判断指标，炉膛压力与锅炉燃料量和送风量之间存在着高通特性.

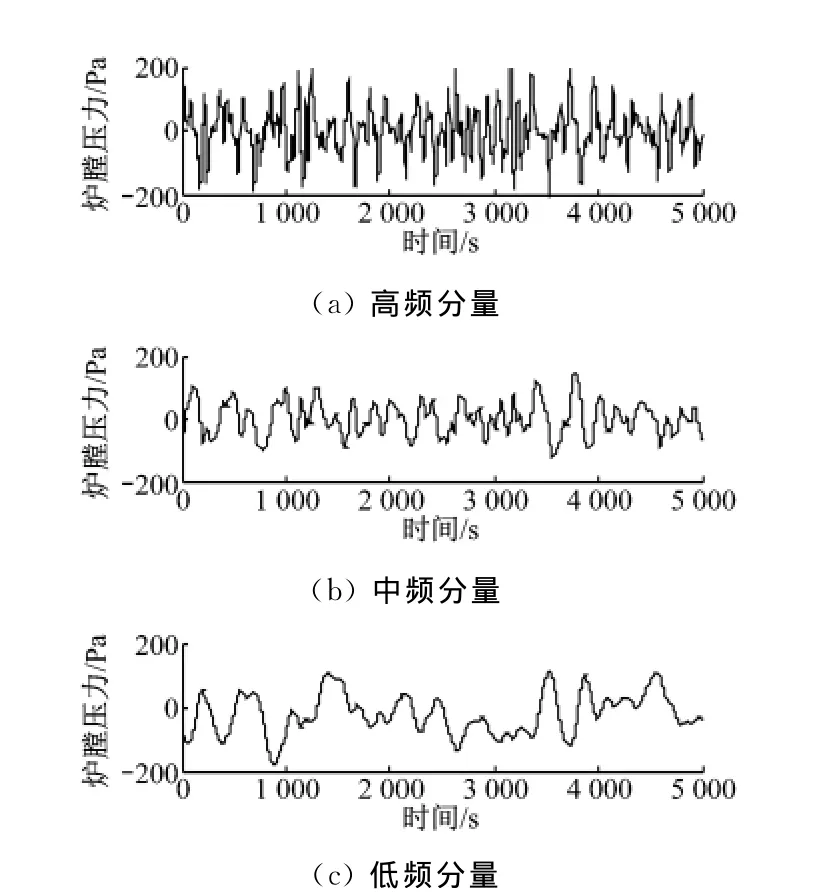
图1 炉膛压力的频率分量Fig.1 Frequency component of furnace pressure

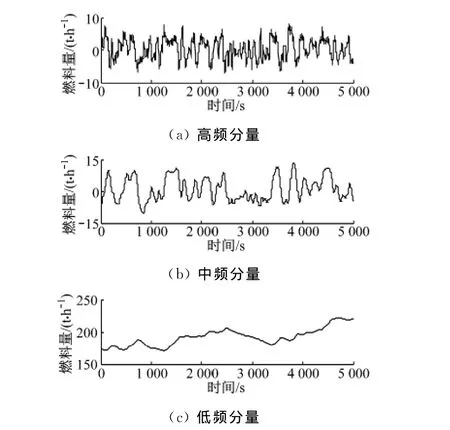
图2 燃料量的频率分量Fig.2 Frequency component of fuel flow

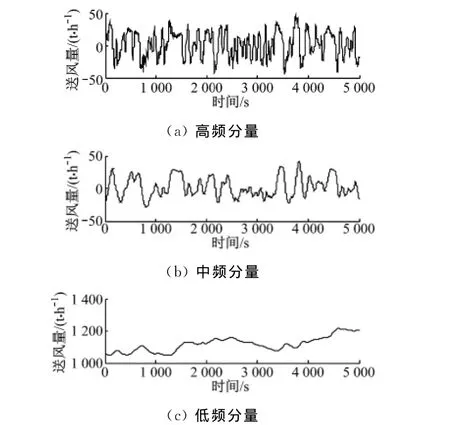
图3 送风量的频率分量Fig.3 Frequency component of forced－draft air flow

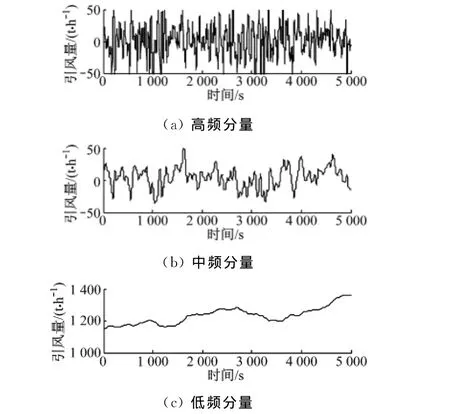
图4 引风量的频率分量Fig.4 Frequency component of induced－draft air flow

3 机理建模

锅炉采用正压直吹式制粉系统和平衡通风设计.虽然燃烧的热力过程比较复杂，但整体上仍然遵循质量守恒定律和能量守恒定律［6］.

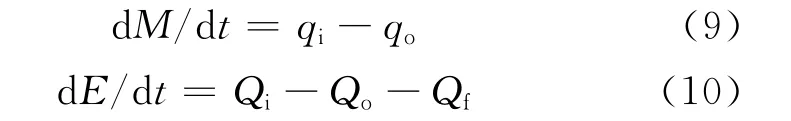
式中：M为炉膛内气体总质量，kg；qi为进入炉膛的工质质量流量，kg／s；qo为流出炉膛的工质质量流量，kg／s；E 为炉膛内气体总存储能量，MJ；Qi为燃料带入炉膛热量和燃烧产生热量之和，MW；Qf为炉膛受热面吸热量，MW；Qo为炉膛出口工质携带热量，MW.

由于建模的目的在于分析对象输入与输出之间的基本动态特性和非线性特性，所以对计算结果绝对精度要求不高［6］，为了避免公式推导过程过于复杂，建模过程进行以下合理简化：

（1）锅炉运行中风煤配比随负荷变化，但近似认为风煤比为常数.

（2）实际烟气比热容随温度变化，近似认为炉膛出口烟气比热容cg1与炉膛内烟气平均比热容cg2相等，即为cg.

（3）实际炉膛内烟气平均温度Thy介于理论燃烧温度Ta与炉膛出口烟温T之间，这里取Thy＝T，同时假设炉膛辐射受热面温度一致.

（4）忽略炉膛及尾部烟道漏风，并且忽略烟气中固体物质的体积.

进入炉膛的物质包括煤粉、一次风、二次风和燃尽风，大型锅炉二次风及燃尽风风量控制多采用带氧量校正的燃料－空气系统控制方案，当风煤比确定时，可以用燃料量表示进入炉膛的煤粉量和总风量.

式中：uB为燃料量，kg／s；K1为系数.

进入锅炉炉膛的热量为

式中：qc为燃料发热量，MJ／kg，近似取常数；h1为燃料的平均比焓，MJ／kg；K2为折算系数.

工质带出炉膛的热量为

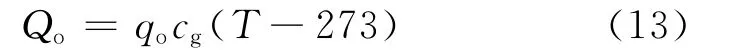
炉膛受热面吸收的热量为

式中：Tb为炉膛受热面平均温度，K，可认为是常数；K3为与炉膛黑度和炉膛结构有关的系数.

由于温度很高，压力相对较低，炉膛内气体可近似认为是理想气体［12］，根据理想气体状态方程有

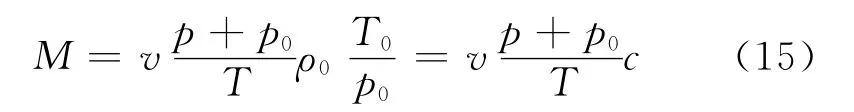
式中：v为炉膛及烟道总体积，m3；ρ0为标准状态下炉膛内烟气平均密度，取值为1.35kg／m3；p为炉膛压力，Pa；T0＝273K；p0＝101 325Pa；c为折算系数，取值为0.003 64.

炉膛内气体总存储能量为

将式（11）～式（16）分别代入式（9）和式（10），求偏导数后得

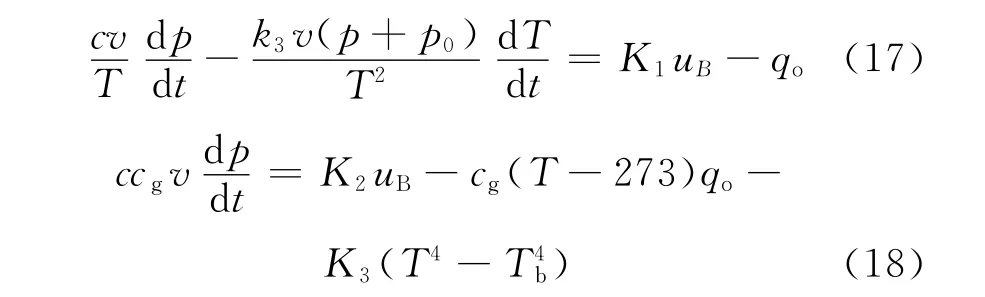
将式（18）代入式（17），经过化简后可得

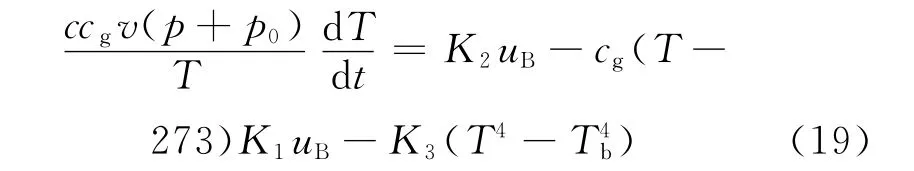
式（18）和式（19）建立了炉膛压力、炉膛温度与锅炉给煤量、引风量的简化非线性动态模型.模型中各项物理意义为：K2uB为燃料带入锅炉炉膛的能量；cg（T－273）K1uB为炉膛出口烟气携带的热量；K3（T4－T4b）为炉膛辐射换热量.

针对600MW 火电机组 HG－2023／17.6－YM4型锅炉，根据100%汽轮机热耗考核工况（THA工况）下的设计数据确定模型参数：K1＝6.4m3／kg；K2＝22MJ／kg；K3＝2.645×10－10；Tb＝700K；cg＝0.001 8MJ／m3；v＝26 000m3.锅炉运行参数为：uB＝68kg／s；qo＝435m3／s；p＝－100Pa；T＝1 300K.

与锅炉设计中的相似性理论求解方法相比，此模型炉膛出口烟温、燃料带入锅炉能量、炉膛出口烟气携带热量、炉膛辐射换热量在50%～100%负荷范围内的相对误差均小于5%.虽然建模过程进行了一些简化，但模型静态精度能够满足简化非线性动态建模的要求.

4 模型分析

大型锅炉常常通过调整引风机静叶角度改变引风量来控制炉膛压力，执行机构惯性时间约为20s，系统采用单回路PID控制方案.针对此系统，在Matlab环境下建立仿真模型并且整定PID控制器参数.然后，分析燃料量与炉膛压力、炉膛温度之间的动态关系.图5给出了在炉膛压力受控情况下，燃料量阶跃增加0.5%时炉膛压力和炉膛温度的响应曲线.

炉膛压力受燃料量的动态增益影响很大，图5中燃料量的变化为0.4t／h，引起的炉膛压力波动超过50Pa.实际上一次风粉气流中煤粉浓度存在剧烈波动，必然导致燃烧状态发生扰动，从而使得炉膛压力发生波动［7］.另外，小幅的燃料量扰动对炉膛温度的影响很小，这与锅炉实际运行情况相符.

图5 炉膛压力和温度随燃料量变化的响应Fig.5 Response of furnace pressure and temperature to the variation of fuel flow

采用经典频域法分析进入炉膛燃料量与炉膛压力之间的关系.图6表示在不同负荷下炉膛压力对燃料量传递函数的幅频特性曲线.由图6可知，炉膛压力与燃料量间的传递函数表现出带通滤波特性；虽然模型存在明显的非线性，但对进入炉膛燃料量与炉膛压力之间传递函数的影响并不明显.

对于火电机组，燃烧扰动是影响炉膛压力、汽包水位、过热和再热汽温、主蒸汽压力等机组主要参数的关键因素.由于调节回路中被控对象往往存在较大的惯性和迟延，仅依靠反馈控制无法获得良好的控制效果.为了消除燃烧扰动，许多控制方案将燃料量作为前馈信号构成前馈－反馈复合控制系统，直吹式制粉系统锅炉往往采用给煤量或总风量信号代表燃料量信号.由于制粉系统存在惯性和迟延，并且在运行过程中存在很多扰动，实际上给煤量或送风量并不能代表进入炉膛的燃料量，因而这些方案不能达到满意的控制效果.

分析表明，炉膛压力能够在一定频带和较宽负荷范围内反映进入锅炉炉膛内燃料量的变化，由于煤粉在炉膛内的燃烧非常迅速，实际上意味着炉膛压力能够在一定程度上实时地反映锅炉燃烧扰动.根据文献［12］的思路和文献［13］的方法，可以构造出静态精度高且动态特性好的锅炉燃烧率信号，为控制系统消除燃烧扰动提供了一种新的思路.

5 结 论

借鉴小波变换多尺度分析的思想，提出一种首先通过多尺度滤波器将信号分解为不同频率范围的分量，然后再进行各分量间线性相关分析的方法.通过分析与炉膛压力相关的信号，发现炉膛压力与燃料量、送风量、引风量之间存在着特定的相互作用关系.机理分析表明：炉膛压力信号与锅炉燃烧率之间具有带通滤波特性，炉膛压力能够在较大负荷和一定频率范围内反映锅炉燃烧状态的变化，揭示了燃料量的瞬时波动是造成炉膛压力剧烈波动的根本原因.

［1］郝祖龙，刘吉臻，常太华，等.基于小波变换的热工信号多尺度相关性分析［J］.中国电机工程学报，2010，30（14）：109－114.HAO Zulong，LIU Jizhen，CHANG Taihua，et al.A－nalysis on multi－scale correlation of thermal signal based on wavelet transform ［J］.Proceedings of the CSEE，2010，30（14）：109－114.

［2］刘吉臻，朱红路，常太华，等.基于最小均方自适应滤波器的热工过程建模方法［J］.中国电机工程学报，2010，30（5）：107－112.LIU Jizhen，ZHU Honglu，CHANG Taihua，et al.Modelling method of thermal process based on least mean square adaptive filter ［J］.Proceedings of the CSEE，2010，30（5）：107－112.

［3］黄景涛，马龙华，茅建波，等.基于支持向量回归的300MW电站锅炉再热汽温建模［J］.中国电机工程学报，2006，26（7）：19－24.HUANG Jingtao，MA Longhua，MAO Jianbo，et al.Modeling research of the reheat steam temperature of 300MW boiler based on support vector regression［J］.Proceedings of the CSEE，2006，26（7）：19－24.

［4］韩璞，乔弘，王东风，等.火电厂热工参数软测量技术的发展和现状［J］.仪器仪表学报，2007，28（6）：1139－1146.HAN Pu，QIAO Hong，WANG Dongfeng，et al.Development and current status of thermal parameter soft－sensing technique in power plant［J］.Chinese Journal of Scientific Instrument，2007，28（6）：1139－1146.

［5］马骏，余岳峰，范浩杰.基于频谱分析和自组织神经网络的火焰燃烧诊断研究［J］.动力工程，2004，24（6）：852－856.MA Jun，YU Yuefeng，FAN Haojie.Research on flame detection and combustion diagnosis based on spectrum analysis and with self organized neural networks［J］.Journal of Power Engineering，2004，24（6）：852－856.

［6］张师帅，周怀春，彭敏，等.基于炉膛辐射能信号的电站燃煤机组燃烧控制研究［J］.中国电机工程学报，2002，22（11）：156－160.ZHANG Shishuai，ZHOU Huaichun，PENG Min，et al.A study on combustion control of a coal－fired power generation unit based on furnace radiant energy signal［J］.Proceedings of the CSEE，2002，22（11）：156－160.

［7］ÅSTRÖM K J，BELL R D.Drum－boiler dynamics［J］.Automatica，2000，36（3）：363－378.

［8］田亮，曾德良，刘吉臻，等.简化的330MW机组非线性动态模型［J］.中国电机工程学报，2004，24（8）：180－184.TIAN Liang，ZENG Deliang，LIU Jizhen，et al.A simplified non－linear dynamic model of 330MW unit［J］.Proceedings of the CSEE，2004，24（8）：180－184.

［9］TAN Wen，FANG Fang，TIAN Liang，et al.Linear control of a boiler－turbine unit：analysis and design［J］.ISA Transactions，2008，47（2）：189－197.

［10］柳艳红，魏学业，王大虎.一种新型的基于相关特性的信号重构算法［J］.仪器仪表学报，2006，27（5）：465－469.LIU Yanhong，WEI Xueye，WANG Dahu.A new signal reconstruction algorithm based on correlation characteristics［J］.Chinese Journal of Scientific Instrument，2006，27（5）：465－469.

［11］曾庆虎，邱静，刘冠军，等.基于小波相关滤波－包络分析的早期故障特征提取方法［J］.仪器仪表学报，2008，29（4）：729－733.ZENG Qinghu，QIU Jing，LIU Guanjun，et al.Approach to extraction of incipient fault features based on wavelet correlation filter and envelope analysis［J］.Chinese Journal of Scientific Instrument，2008，29（4）：729－733.

［12］于达仁，范轶，徐志强.基于分布信息融合的直流锅炉燃料量信号重构［J］.中国电机工程学报，2004，24（2）：191－195.YU Daren，FAN Zhi，XU Zhiqiang.Reconstruction for fuel signal of once－through boiler based on distributed data fusion［J］.Proceedings of the CSEE，2004，24（2）：191－195.

［13］田亮，刘鑫屏，赵征，等.一种新的热量信号构造方法及实验研究［J］.动力工程，2006，26（4）：499－502.TIAN Liang，LIU Xinping，ZHAO Zheng，et al.Experimental research of a new kind of signal for amounts of heat released［J］.Journal of Power Engineering，2006，26（4）：499－502.