基于特征序列匹配函数的快速图像匹配
2012-06-23郑兴明
郑兴明
(南京航空航天大学计算机科学与技术学院,江苏 南京 210016)
利用图像信息对目标物体进行搜寻和攻击,在当前越来越受到重视,特别是在航空航天、军事打击、医学手术中的应用,其准确性,精确性和实时性一直是该领域的主要研究方向。图像信息除了包含内容的局部信息,还包含内容之间相互关系的全局信息,局部信息特征表述了目标特征区域的信息,如图像的直线、颜色特征、角度、轮廓以及这些特征之间的相互关系。全局特征描述的是整个图像的信息,如图像的灰度直方图等。图像全局特征信息在某些细节上淡化了局部目标区域的细节特征,不能体现匹配的结果,利用图像的局部特征进行匹配越来越受到重视,并成为计算机视觉领域的热点。
目前针对图像匹配的主要方法有基于像素点匹配的归一化积相关灰度匹配、序贯相似性检测匹配(Similarity Sequential Detection Algorithm,SSDA)、基于特征匹配的[1](Scale - Invariant Features Transform,SIFT)和仿射不变特征点提取方法 Harris- Affine[2-4]。模板匹配的主要思想是将待匹配的图像作为模板图像,以窗口的方式,在待查找的源图像中扫描一遍,通过该模板所对应区域的图像与模板图像之间的相似距离来判断识别的结果。序贯相似性检测匹配主要解决模板匹配算法计算量大的问题,模板匹配每滑动一次就要做一次匹配运算,除了匹配点外在其他匹配点做了“无用功”,导致匹配算法计算量上升,一旦发现所在的参考位置为非匹配点,立刻换到新的参考点计算,加大匹配速度。SIFT方法能够从匹配图像中提取显著不变特征,使不同视角目标或场景图像稳定匹配,该特征向量对图像尺度、旋转变化、噪声和光照变化不敏感。由于SIFT对目标遮挡和图像混杂稳定性较强,因此在目标识别中取得良好效果。仿射不变特征方法主要解决大视角变化的图像匹配问题,在仿射高斯空间的基础上,用多尺度Harris特征点,检测算子提取适应仿射变换的特征点,然后用特征点的椭圆邻域代替圆形邻域。通过迭代估计特征点邻域的仿射形状,不断调整特征点所在的尺度、位置和形状收敛直到不变为止,最终得到仿射不变特征向量。利用像素点进行匹配的主要缺陷是计算量过大,对图像的灰度变换敏感,尤其是非线性的光照变化。此外,对目标的旋转,变形以及遮挡也比较敏感[5]。因而基于像素点匹配的方法不适合实际场景中的应用,为克服这些缺点,可以利用图像的特征进行匹配,一方面图像的特征点比像素点要少,减少了匹配过程的计算量。另一方面局部特征点[6]的匹配度量值对位置的旋转、变形以及遮挡不是很敏感,可以大大提高匹配的精度。而且特征点的提取过程可以减少噪声的影响,对灰度变化,图像变形以及遮挡等有较好的适应能力。文中采用失配函数的思想,解决像素点计算量过大的缺陷,同时利用局部特征匹配的优势,提高图像匹配的精确度和执行速度。
1 尺度不变特征
尺度不变特征(Scale-Invariant Feature Transform,SIFT)是一种计算机视觉用于侦测与描述图片中局部特征的,它在空间尺度中寻找极值点,并提取出其位置、尺度、旋转不变量等相关特征。
局部特征的描述与侦测可以帮助识别物体,SIFT特征是基于物体上一些局部外观的兴趣点,而与影像的大小和旋转无关。对于光线、噪声、些微视角改变的容忍度较高。基于这些特性,它们是高度显著而且相对容易撷取,在庞大的特征数据库中,容易辨识物体且鲜有误认。使用SIFT特征描述对于部分物体遮蔽的侦测率也较高,甚至只需要3个以上的SIFT物体特征就能计算出位置与方位。在现今的计算机硬件速度下和小型的特征数据库条件下,辨识速度可接近即时运算。SIFT特征的信息量大,适合在海量数据库中快速准确匹配。
SIFT架构中的特征点是利用不同尺度下高斯滤波器(Gaussian Filters)进行卷积(Convolved),然后利用连续高斯模糊化差异,根据不同尺度下的高斯差(Difference of Gaussians)中最大最小值导出,其公式如下

其中,L(x,y,kiσ)是在尺度 kiσ 的条件下,由原始图像I(x,y)与高斯模糊 G(x,y,kσ)进行卷积

G(x,y,kσ)是尺度可变高斯函数

为减少噪声对特征点的影响,避免将边缘附近的点也误认为是特征点,采用Hessian[7]矩阵对极值点进行过滤,其公式如下
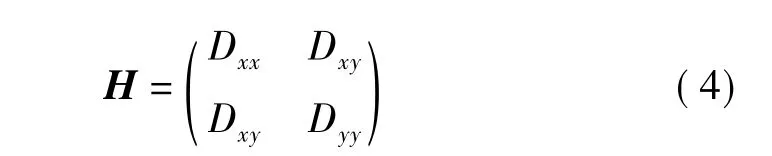
在得到特征点的尺度和位置信息后,为使特征点描述向量对旋转不变,需要为特征点分配角度信息。计算特征点梯度大小 m(x,y)和角度 θ(x,y)。
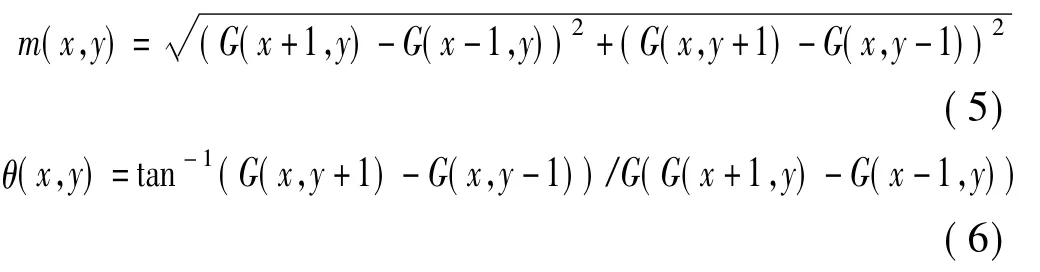
最后利用特征点的梯度方向构建一个36 bin的角度直方图,直方图的峰值代表局部梯度的主方向。以特征点为中心取16×16个像素的窗口,分成16个4×4的子块,在每个 4 ×4 的子块上计算 0°,45°,90°,135°,180°,225°,270°,315°这 8 个方向的梯度大小和梯度方向直方图。因此,一个4×4的子块可以得到一个8方向描述符,则16个4×4的子块可以得到128个方向描述符,这个1×128的向量就定义为特征描述符向量。如图1所示分别在不同像素下提取的SIFT匹配特征,图1(a)是相同大小测试图像和匹配图像,分辨率较低,其特征点的个数只有5个,图1(b)特征点的个数为32个,图1(c)特征点个数为43个,图1(d)特征点个数为106个。
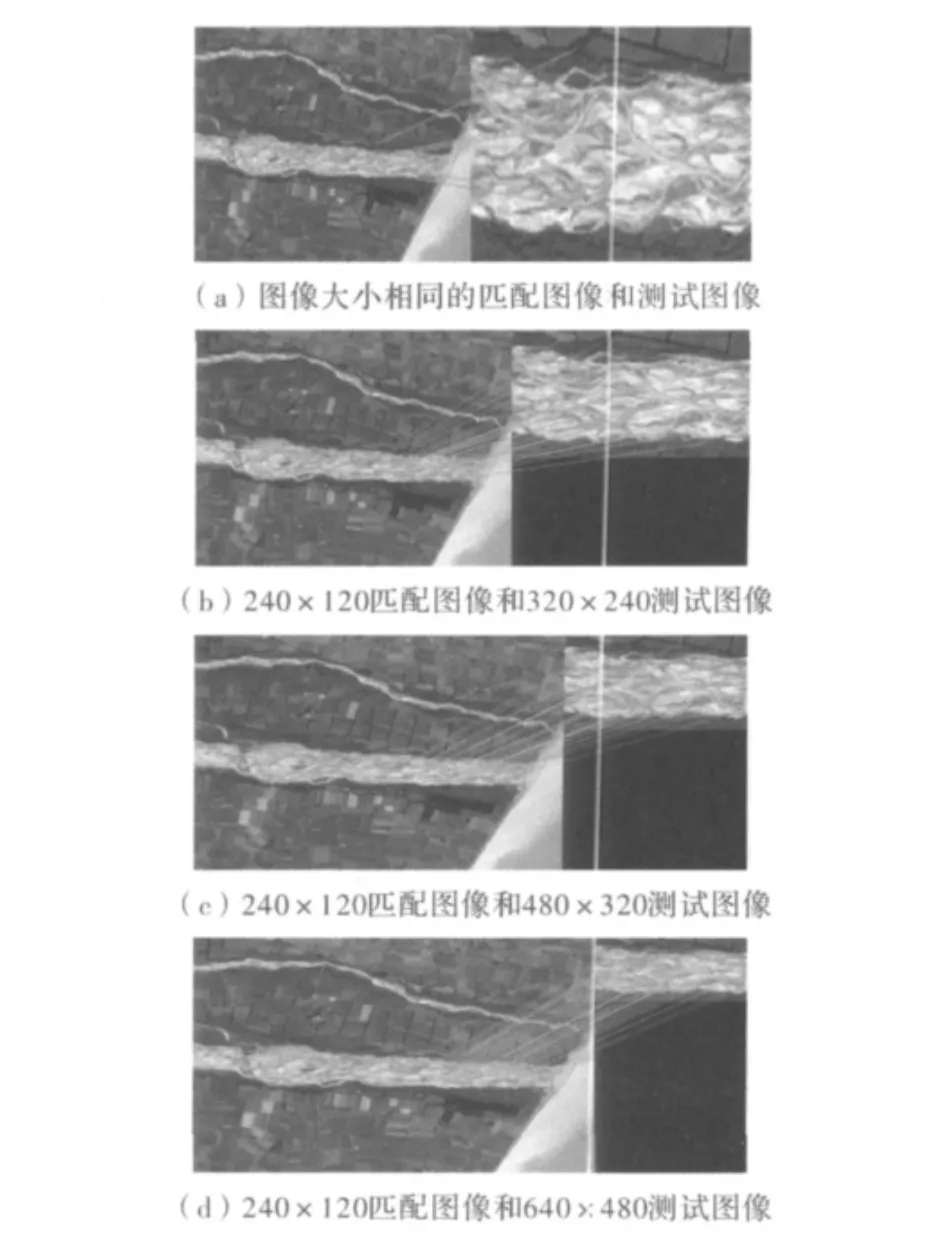
图1 SIFT在不同分辨率图像下的特征匹配
2 匹配函数
文中提出的匹配函数[8]是利用匹配本身的特征信息来决策出重新进行匹配的起始点。假设特征序列构成的描述符向量可以表示为一串由字母组成的字符串:P=abcabcacab,同样查找图像的特征序列也被表示成一串很长的字符串:S=…abacbdfe…,问题转变为在主串S中查找出是否具有P特性的匹配串。
令S=s0s1…sm-1是主串,要确定P是否在si开始处匹配。如果si≠a则接下来显然要用si-1与a比较。同理,若si=a且si+1≠b,则接下来要用si+1与a比较。若sisi+1=ab且si+2≠c,则有以下情形

其中,“?”表示S在该位置的值是多少无关紧要。第一个“?”表示si+2且si+2≠c,下一次应该用P的第一个字符直接与si+2比较,而不是与si+1比较,因为P的特征序列的第2个字符b与S中si+1相等,一定有si+1≠a。假定P的前4个特征字符和S匹配,但下一个特征字符失配,即si+4≠b

此时应该用si+4与P的第2个特征字符进行比较,等效于把P向右滑动,使它的子串对准S的一个子串,然后比较两个相等子串后面的第一个字符。可以得出,根据特征字符串P中的字符信息,以及匹配失效主串的字符位置,可以确定接下来应该用特征字符串中的哪个特征字符和主串的当前失配字符继续比较,而无需回去比较主串的较前位置字符。
特征串p=p0p1…pn-1的匹配函数定义为

由定义可得,如果部分匹配结果是 si-j…si-1=p0p1…pj-1且 si≠pj,则接下来如果 j≠0,应该用 si与pf(j-1)+1相比;如果 j=0,用 p0与 si+1相比。
3 算法执行
图像匹配的过程是目标图像在测试图像中查找相似特征的目标。首先将目标图像分割,假设目标图像的大小是M×N,对图像长M进行m等分,对图像宽N进行n等分,这样目标图像就被分割成m×n个大小模块的子图像,每个子图像的大小为,同样对测试图像进行相同的处理。处理结果如图2所示。

图2 分割为m×n大小的目标图像
分割好的目标图像分别计算SIFT局部特征,将计算完的特征按照图像字块的顺序从左到右从上到下排列成一行序列,其长度为m×n,目标图像就被表示成了一串具有SIFT特征的序列串,每个串的值代表了当前分块子图像的细节特征表述,如图3所示。

图3 SIFT提取映射后的特征序列
分块子图像的SIFT特征是1×128个特征向量描述符。它包含了该子图像的特征信息,由于每个子图像包含的细节不相同,保证了特征序列间没有太大的关联性,同时子图像内容之间是连续的,特征序列之间又保持着关联性。同样测试图像也按照上述方法进行分割,在测试图像匹配目标图像就转变到在测试图像特征序列里查找目标图像的特征序列,SIFT提取出的特征向量表述符之间的相似性采用欧氏距离的来确定,设置某一阈值σ,当特征向量之间的欧氏距离<σ时,判定这两个特征向量之间是相似或者相近的,当特征向量之间的欧氏距离>σ时,判定该特征向量之间不匹配,利用匹配函数重新定位新的匹配点,重新进行匹配,直至测试图片整个特征序列结束。
算法执行流程如下:
(1)初始化测试图片和目标图片,分别将其转化成灰度图像。
(2)测试图片和目标图片分别分割成具有相同大小的子图像,并按图像内容组织成一行序列。
(3)分别对上述一行序列进行SIFT特征提取,以向量的形式存储。
(4)计算测试图片的特征序列和目标图片的特征序列是否相近或相似,如果相似则继续匹配,否则转到(5)。
(5)利用匹配函数计算出在测试图片中失效匹配点重新匹配的位置,重复(4)。
(6)测试图像特征序列结束,输出匹配序列。
4 实验结果
本方法利用SIFT对目标分割子图像进行特征提取,将提取出的特征按照子图像分割的序列进行重构,目标图像和测试图像就转换成一行具有特征描述符的序列,对特征描述符进行匹配函数计算,进行匹配过程。图片大小直接影响到子图像的分割和特征序列的生成,同时提高各个子图像不同的特征序列之间的差异性,实验图片选取分辨率较高的1500×1500的测试图片和分辨率为300×300的目标图片,子图像的大小为15×15,这样测试图片就被划分为10000个特征序列,目标图像被划分为400个特征序列。特征序列之间的相似度和相近程度用欧氏距离来确定,实验的过程中欧氏距离的误差阈值σ≤20,当欧氏距离在这个范围内,特征图片匹配。实验一方面从单张图片匹配结果进行讨论,另一方面从单张图片在模板匹配方法,序贯相似性匹配方法和SIFT本身匹配进行比较。图4显示的是匹配的结果,图4(b)中灰色区域为匹配的目标区域,如图5所示,黑色为匹配结果,从图中可以看出,除了目标区域被匹配,其他区域也被匹配,实验过程中为了降低匹配函数带来的负面影响,在最优情况下连续20个特征序列匹配,该20个特征序列就是匹配的区域,匹配过程中产生的其他匹配是因为在该20个特征序列内,其相似程度的欧氏距离都小于阈值σ≤20,由于增大了连续匹配成功的特征序列的长度以及减小特征序列的相似度的阈值,使得匹配的结果较为合理。实验的目标区域特征为房屋建筑,具有棱角和直线的特征,在区域划分很小的情况下很难区分出来,导致结果在房屋建筑上匹配有误差。

图4 分辨率为的测试结果

图5 目标图片
匹配函数在目的上解决了重新匹配的新配点的计算,同时又是以局部特征为匹配,而不是以单纯的像素点来匹配,加大了匹配的速度,其匹配执行速度要高于模板匹配,序贯相似匹配方法和SIFT本身匹配进行比较,表1显示了在上述匹配方法执行速度。

表1 3种匹配方法的执行速度
5 结束语
文中主要利用提出的匹配函数来对图像匹配进行快速匹配,加快图像匹配的速度,关键点在于子图像的划分和局部特征提取,子图像的大小直接影响到局部特征的提取,子图像太小,局部细节丢失严重,特征序列之间的相关性丢失,匹配函数匹配重复计算率提高,子图像太大,特征序列之间相关性过大和宽度过短,匹配函数不起作用。局部特征提取才用SIFT特征提取,一方面SIFT特征在全局图像匹配中具有良好的匹配结果,在其基础上加快处理速度。因子图像的划分和相似度的阈值是根据仿真和先验只是初步估算,接下来的工作主要研究子图像大小的划分和局部特征的提取,从图像本身特征的角度自适应划分子图像的大小以及对其局部特征的提取。
[1]LOWE D G.Distinctive image features from scale- invariant keypoints[J].International Journal of Computer Vision(S0920 -5691),2004,60(2):91 -110.
[2]MIKOLAJCZYK K,CORDELIA S.Scale & affine invariant interest point detectors[J].International Journal of Computer Vision(S0920 -5691),2004,60(1):63 -86.
[3]MIKOLAJCZYK K,TUYTELAARS T,SCHMID C,et al.A comparison of affine region detectors[J].International Journal of Computer Vision(S0920 - 5691),2005,65(1):43-72.
[4]MIKOLAJCZYK K,CORDELIA S.A performance evaluation of local descriptors[J].IEEE Transactions on Pattern Analysis and Machine Intelligence(S0162 - 8828),2005,27(10):1615-1630.
[5]ZHAO Zhenbing,WANG Rui.A method of infrared/visible image matching based on edge extraction[C].International Congress on Image and Signal Processing,2010:871 -874.
[6]田金文,杨磊.基于局部分形特征的快速图像匹配方法[J].华中理工大学学报,1996,24(2):12 -14.
[7]刘小军,杨杰.基于主成分分析的放射不变特征图像匹配方法[J].系统仿真学报,2004,20(4):977 -980.
[8]ELLIS H,SARTAJ S.Fundamentals of data structures in C[M].2 ed.,Berlin:Springer Press,2003.
