玻璃质微通道流动阻力特性的数值模拟

周萍，陈卓，徐则林，莫景文

(中南大学 能源科学与工程学院，湖南 长沙，410083)

玻璃因其特殊的物理化学性能，广泛应用于封装、射频微机电以及生物芯片基座等微流控系统中，因此，基于玻璃材质的微加工工艺也就成为开发微流控系统的一个重要技术问题。玻璃微通道的刻蚀方法主要有机械刻蚀、干法刻蚀(等离子刻蚀)与湿法刻蚀三大类。机械刻蚀包括传统钻刻、超声钻刻、电化学加工和喷粉法等，其缺点是无法得到较光滑的刻蚀表面。干法刻蚀的刻蚀成本高，刻蚀速率低，刻蚀面的表面粗糙度也较高[1]，因此，目前使用最广泛的仍是湿法刻蚀。湿法刻蚀是利用氢氟酸对玻璃的腐蚀性对控制面的玻璃进行腐蚀。由于玻璃各向同性的特征，刻蚀一般无法得到严格的矩形微通道截面形状，而是侧壁为圆弧形的通道[2-3]，本文将这种截面形状的微通道称为圆角形微通道。同时，由于刻蚀的横向速度远远大于纵向速度，因此，用一般湿法刻蚀方法得到的微通道截面大多宽度大于深度。虽然许多研究用复杂工艺可以得到玻璃湿法刻蚀的较理想矩形通道截面[4-5]，但由于经济性较差，目前尚无法用于批量生产。另一方面，在微流控系统设计中，阻力是非常重要的1个参数，其大小在很大程度上取决于微通道的截面形状及其内部流动特征(层流、湍流以及过渡流)，常用范宁阻力系数来表示，即

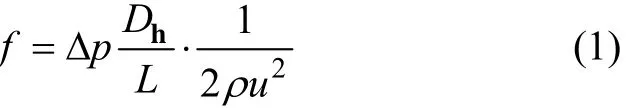
式中：Δp为微通道压降；Dh为截面特征尺度；L为微通道长度；ρ为流体密度；u为流体流速。

范宁阻力系数(f)与雷诺数(Re)的乘积称为Poiseuille数(简称 Po数，Po=f·Re)。对于圆管层流，Po是1个常数，其值为16；对于矩形通道，Po是1个与微通道截面形状因子有关的量，Shah等[6]提出了在低雷诺数下Po的经验公式，即：

微通道中流体的压降受流动状态、流体性质、通道截面形状等众多参数的影响，过去对该问题的研究主要集中在几个方面：

(1) 流体性质对微通道流动特性的影响。Wu等[7-8]对不可压缩和可压缩氮气、氢气和氩气的流动进行了研究；Yang等[9]对不可压缩空气的流动进行了研究；Judy等[10]研究了异丙醇、水和甲醇的流动；Yang等[9,11]研究了R134a液体和R114液的流动。

(2) 截面形状对微通道流动特性的影响。Celata等[11]对圆形截面、马璨等[12]对矩形截面进行了研究，蒋炳炎等[13]对三角形和梯形截面微通道内流动特征进行了研究。

(3) 管壁对微通道流动特性的影响。王玮等[14-16]通过研究发现，粗糙管壁会增加层流区的阻力系数以及引起层流向湍流提前转变。

(4) 流动状态对微通道流动特性的影响。

不同研究者分别对层流、过渡区流动和湍流流动[17]以及微通道内的两相流[18]，滑移流动[19]等进行了研究。已有研究工作主要是针对圆形、矩形、三角形、梯形等规则截面形状的微通道而进行的。对于实际玻璃湿法刻蚀得到截面形状的微通道阻力特性的研究尚未见相关文献报道。微通道流动特性的研究方法主要有实验研究与数值模拟两大类。实验研究方法由于存在成本高、周期长以及参数检测困难等问题而使其应用受到很大的限制，数值模拟方法则由于具有成本低、周期短以及模拟能力强的特点，近些年在微通道流动的研究领域得到了广泛应用[20-21]。为此，本文作者采用数值模拟的方法，以水为介质，研究低雷诺数下圆角型微通道的截面形状对阻力系数的影响规律，并拟合出Po准数与界面形状因子α之间的关联式，为微通道流动特性的研究及其工程应用提供理论依据。

1 玻璃质微通道几何结构及其网格划分

根据湿法刻蚀的特点，数值模拟中对微通道截面形状进行适当简化处理。设两侧壁为1/4圆弧面，底面为平面(见图1)，且截面最大宽度D大于高度H。定义高H(亦即圆弧所在圆的半径)与底部直段长W的比值为截面形状因子α，

结合作者前期工作，取微通道的宽度 D为 200 μm，长度L为3 000 μm。考虑W与H为8种不同尺寸即 8种不同的形状因子，其具体的几何参数见表1。

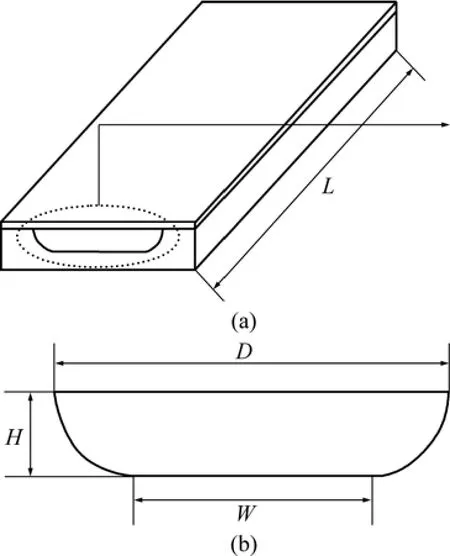
图1 圆角形微通道几何形状示意图Fig.1 Schematic diagram of geometry for semi-circle microchannel

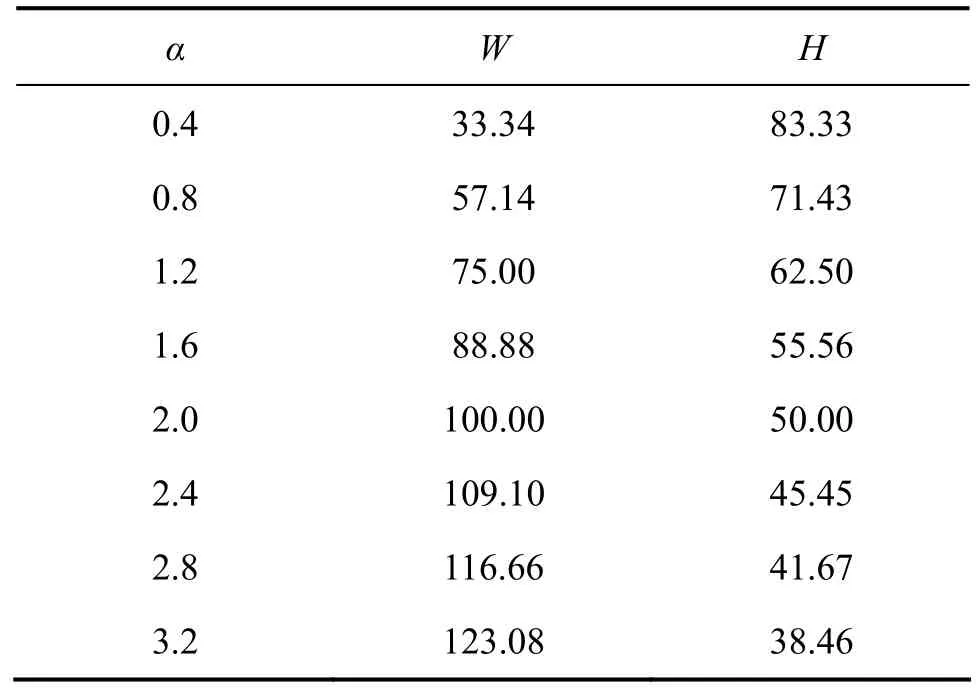
表1 不同形状因子α的圆角形微通道几何参数Table 1 Geometric parameters of microchannels with different aspect ratios μm

对微通道的解析区域采用结构化网格划分，且对壁面处的网格加密以更好地处理边界层流动现象，使求解更精确。根据微通道截面几何尺寸的不同，所划分的总网格数为5.0×105～7.0×105，并对网格独立性进行验证。

2 数学模型及其边界条件

2.1 数学模型

在对微通道流动过程进行数值模拟时，作出以下假设：(1) 流体为牛顿流体；(2) 流动过程为等温稳态过程；(3) 流体为不可压缩流体，且为层流流动(0.01＜Re＜40)；(4) 流体在壁面附近为无滑移流动；(5) 对于分子自由程小于10-3μm的流体，当微通道特征尺度大于1 μm时，均能满足克努曾准数Kn＜10-3，流动不受稀薄效应影响，可以使用连续介质假设[22]。所研究的微通道特征尺度均在30 μm以上，故其内部流体流动可视为连续流动。

基于上述假设，描述微通道内流体流动过程的控制方程如下。

连续性方程：

动量方程：

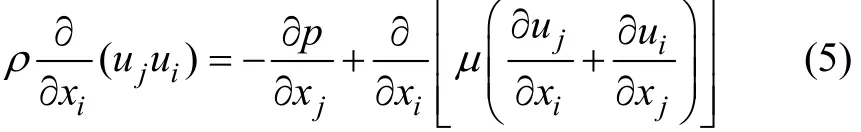
其中：ui为i方向上的速度分量，且i和j 均为1，2和3，代表x，y和 z 3个坐标方向；p为静压；ρ和μ分别为流体的密度和动力黏度。

2.2 边界条件

微通道中的流动介质为水，温度为定常值(293 K)，其密度 ρ=998.2 kg/m3，动力黏度 μ=1.004×10-3Pa·s；流体入口为速度入口边界条件，壁面为无滑移边界条件；出口为压力出口。

3 结果与讨论

基于 FLUENT6.3软件平台，以圆形截面微通道内流体阻力的理论计算公式为基准，对微通道内流体阻力数值模拟的模型与方法的有效性进行检验。在此基础上，对截面形状因子对圆角形微通道内流动阻力的影响规律进行数值模拟研究。

3.1 雷诺数和截面形状因子对微通道压降的影响

根据文献[23]和[24]中的研究经验，对 0.01≤Re≤40时水在圆角形微通道内的流动进行研究。针对微通道截面最大宽度D大于高度H的特点，取微通道的高度H为雷诺数的特征尺度[22]，且雷诺数的定义式为：

式中：um为微通道截面平均流速。基于不同雷诺数与截面形状因子的微通道流动过程的数值模拟结果，为排除入口和出口效应的影响，由管流充分发展段计算出单位长度压降，并分别绘出微通道单位长度压降随雷诺数、截面形状因子变化的曲线，见图2和图3。

由图2可知：不同截面形状因子下圆角形微通道单位长度压降均随雷诺数的增加而增加，且呈线性变化，这与常规层流流动阻力的规律相同。图3表明：截面形状因子对玻璃质微通道流动阻力有重要影响；在微通道截面的最大宽度D一定的情况下，不同雷诺数下微通道单位长度压降均随着截面形状因子的增加而增加，且呈现出非线性变化的趋势。

图2 定宽度时雷诺数Re对微通道单位长度压降p的影响Fig.2 Effect of Re on micro-channel pressure drop at a constant width

图3 定宽度时微通道形状因子α对单位长度压降p的影响Fig.3 Effect of micro-channel shape factor on pressure drop at a constant width

3.2 雷诺数和截面形状因子对微通道Po数的影响

由式(1)与(6)可得：

研究结果表明：当截面形状因子一定时，不同雷诺数下的Po重合在一起(如图4所示，7个雷诺数条件下的数据点重合)，说明Po并不随Re的变化而变化，即同一种截面形状因子的微通道流动 Po为一定值。由流体力学理论可知：对于常规不可压缩充分发展段流动，流动阻力系数与雷诺数的乘积与雷诺数无关，因此，这一结果与理论分析相符。可以认为Cui等[24]研究中 Po随雷诺数的波动是实验测量误差等原因造成的。

如图4所示，Po随形状因子的增大而减小，但随着形状因子的不断增大，Po的减小趋势逐渐变缓。这表明形状因子是影响 Po的重要因素，与矩形微通道中的流动特征是相似的[6]。在微通道宽度一定的情况下，Po与单位长度压降随形状因子的变化规律不同。事实上，综合式(1)，(3)和(6)可得：

式中： 为常数。式(8)表明：当宽度与 Re一定时，微通道单位长度压降不仅与阻力系数相关，而且与形状因子相关；而式(7)则仅取决于阻力系数，因此，Po与阻力系数均随形状因子的增大而减小，而单位长度压降随形状因子的变化规律则有所不同。

图4 不同Re下微通道形状因子对Po数的影响Fig.4 Effect of micro-channel shape factor on Po number at different Re

3.3 圆角型微通道阻力系数的经验公式

3.3.1 阻力系数经验公式的拟合

截面形状因子α是影响Po的单一变量。因此，基于图4中0.01≤Re≤40时Po随形状因子的变化规律，通过曲线拟合，得到圆角型微通道阻力系数的经验公式如下：

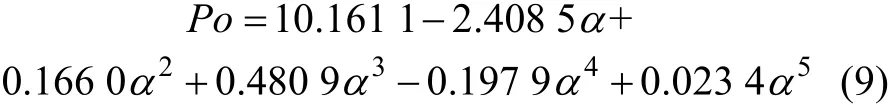
经验公式与数值模拟结果之间的误差不大于0.5%，形状因子α的适应范围为0.4≤α≤3.2。

3.3.2 阻力系数经验公式对不同几何尺寸的微通道适用性

上述研究结果是在通道截面最大宽度一定、截面高度变化的情况下获得的，为验证式(9)的普适性，对截面高度一定(H=50 μm)、截面最大宽度变化的微通道流动阻力特性进行研究。将基于式(9)计算得到的不同形状因子的圆角形微通道 Po预测值与对应参数下的数值模拟结果进行比较后发现：当0.4≤α≤3.2时，雷诺数对圆角型微通道的 Po没有影响，这与前面结果一致；且式(9)计算得到的不同形状因子下的微通道Po预测值与数值模拟结果之间的误差小于0.70%。

3.3.3 阻力系数经验公式对不同黏度流体的适用性

为进一步验证阻力系数经验公式的适用性，使用高黏度的离子液(Bmin)BF4对其进行验证，其物理性质见表2[25]。表3所示为形状因子为2.0和不同雷诺数下基于式(9)的 Po预测值与数值模拟结果间的相对误差。由表3可知：最大误差小于0.3%。

因此，可以认为在所研究的雷诺数区域 (0.01≤Re≤40) 和形状因子范围(0.4≤α≤3.2)内，圆角型微通道阻力系数经验公式(9)具有良好的适用性。

表2 离子液(Bmin)BF4物理性质Table 2 Properties of ionic liquid (Bmin)BF4

表3 α=2.0，H=50 μm时离子液微通道流动Po数相对误差分布Table 3 Error distribution of Po of ionic liquid when α=2.0 and H=50 μm

4 结论

(1) 对于圆角型微通道，当截面宽度一定时，雷诺数与截面形状因子均对压降有很大影响，且压降随雷诺数和形状因子的增大而增大。

(2) 当雷诺数0.01≤Re≤40时，同一截面形状因子的圆角形微通道 Po与随雷诺数无关，因此，截面形状因子是圆角形微通道 Po的影响单一参变量，且其Po随截面形状因子的增大而减小。

(3) 基于圆角型微通道的数值模拟数据，拟合了Poiseuille数Po随截面形状因子变化的阻力系数α经验公式：Po=10.161 1-2.408 5α+0.166 0α2+0.148 09α3-0.197 9α4+0.023 4α5。该式在雷诺数 0.01≤Re≤40 和截面形状因子0.4≤α≤3.2范围内均适用。

[1] Jansen H, Gardeniers H, de Boer M, et al. A survey on the reactive ion etching of silicon in microtechnology[J]. Journal of Micromechanics Microengineering, 1996, 6(1): 14-28.

[2] Iliescu C, Tay F E H, MIAO Jian-min. Strategies in deep wet etching of Pyrex glass[J]. Sensors and Actuators A: Physical,2007, 133: 395-400.

[3] Saito Y, Okamoto S, Miki A, et al. Fabrication of microstructure on glass surface using micro-indentation and wet etching process[J]. Applied Surface Science, 2008, 254:7243-7249.

[4] LIU Yong-xun, Ishii K, Tsutsumi T, et al. Ideal rectangular cross-section Si-fin channel double-Gate MOSFETs fabricated using orientation-dependent wet etching[J]. IEEE Electron Device Letters, 2003, 24(7): 484-486.

[5] Iliescu C, MIAO Jian-min, Tay F E H. Optimization of PECVD amorphous silicon process for deep wet etching of Pyrex glass[J].Surface and Coatings Technology, 2005, 192: 43-47.

[6] Shah R K, London A L. Laminar Flow Forced Convection in Ducts[M]. New York: Academic Press, 1978: 157.

[7] Wu P Y, Little W A. Measurement of friction factors for the flow of gases in very fine channels used for microminiaturize Joule–Thomson refrigerators[J]. Cryogenics, 1983, 24(8):273-277.

[8] Harley J, Huang Y, Bau H, et al. Gas flow in microchannels[J].Journal of Fluid Mechanics, 1995, 284: 257-274.

[9] Yang C Y, Chien H T, Lu S R, et al. Friction characteristics of water, R134a and air in small tubes[C]//Celata, G P, ed.Proceedings of the International Conference on Heat Transfer and Transport Phenomena in Microscale. New York: Begell House, 2000: 168-174.

[10] Judy J, Maynes D, Webb B W. Characterization of frictional pressure drop for liquid flows through microchannels[J].International Journal of Heat and Mass Transfer, 2002, 45:3477-3489.

[11] Celata G P, Cumo M, Guglielmi M, et al. Experimental investigation of hydraulic and single phase heat transfer in 0.130 mm capillary tube[J]. Microscale Thermophysical Engineering,2002, 6:85-97.

[12] 马璨, 袁惠新, 杨振东, 等. 微反应器矩形微通道截面高宽比对流速的影响[J]. 环境科学与技术, 2009, 32(10): 64-66.MA Can, YUAN Hui-xin, YANG Zhen-dong, et al. Impact of aspect Ratios on Velocity in Rectangular Micro-channel[J].Environmental Science & Technology, 2009, 32(10): 64-66.

[13] 蒋炳炎, 谢磊, 谭险峰, 等. 流道截面形状对微流体流动性能的影响[J]. 中南大学学报: 自然科学版, 2006, 37(5): 964-969.JIANG Bing-yan, XIE Lei, TAN Xian-feng, et al. Influence of section shape of micro channels on microfluid flowability[J].Journal of Central South University:Science and Technology,2006, 37(5): 964-969.

[14] 王玮, 李志信, 过增元.粗糙表面对微尺度流动影响的数值分析[J]. 工热物理学报, 2003, 24(1): 85-87.WANG Wei, LI Zhi-xin, GUO Zeng-yuan. Numerical simulation of rough surface effects on microscale fluid flow[J]. Journal of Engineering Thermophysics, 2003, 24(1): 85-87.

[15] 王昊利, 王元, 刘江.平板微通道壁面粗糙度对流场影响的摄动分析[J]. 西安交通大学学报, 2005, 39(5): 540-543.WANG Hao-li, WANG Yuan, LIU Jiang. Perturbation analysis of wall roughness effect on flow in micro-channel between two parallel plates[J]. Journal of Xi’an Jiaotong University, 2005,39(5): 540-543.

[16] Hrnjak P, Tu X. Single phase pressure drop in microchannels[J].International Journal of Heat and Fluid Flow, 2007, 28: 1-14.

[17] Yang C Y, Wu J C, Chien H T, et al. Friction characteristics of water, R-134a, and air in small tubes[J]. Microscale Thermophysical Engineering, 2003, 7: 335-348.

[18] 吴嘉峰, 陈永平, 施明恒, 等. 矩形微通道中环状冷凝的数值模拟[J]. 工程热物理学报, 2008, 29(11): 1924-1926.WU Jia-feng, CHEN Yong-ping, SHI Ming-heng, et al.Simulation for annular condensation flow in rectangular microchannels[J]. Journal of Engineering Thermophysics, 2008,29(11): 1924-1926.

[19] DUAN Zhi-peng, Muzychka Y S. Slip flow in non-circular microchannels[J]. Microfluidics and Nanofluidics, 2006, DOI 10.1007/s10404-006-0141-4.

[20] QU Wei-lin, Mudawar I. Experimental and numerical study of pressure drop and heat transfer in a single-phase micro-channel heat sink[J]. International Journal of Heat and Mass Transfer,2002, 45: 2549-2565.

[21] Valdés J R, Miana M J, Pelegay J L, et al. Numerical investigation of the influence of roughness on the laminar incompressible fluid flow through annular microchannels[J].International Journal of Heat and Mass Transfer, 2007, 50:1865-1878.

[22] Kandlikar S G, Garimella S, LI Dong-qing, et al. Heat transfer and fluid flow in minichannels and microchannels[M]. Oxford:Elsevier, 2006: 17-21.

[23] Jiang X N, Zhou Z Y, Huang X Y, et al. Laminar flow through microchannels used for microscale cooling systems[C]//Proceedings of the 97 IEEE/CPMT Electronic Packaging Technology Conference. 1997: 119-122.

[24] Cui H H, Silber-Li Z H, Zhu S N. Flow characteristics of liquids in microtubes driven by a high pressure[J]. Physics of Fluids, 2004, 16(5): 1803-1810.

[25] Wilkes J S, Zaworotko M J. Air and water stable 1-ethyl-3-methylimidazolium based ionic liquids[J]. Journal of the Chemical Society, Chemical Communications, 1992(14):965-967.