定日镜群风荷载干扰效应的数值模拟

王莺歌，李正农，卢春玲

(1. 嘉应学院 土木工程学院，广东 梅州，514015；2. 湖南大学 建筑安全与节能教育部重点实验室，湖南 长沙，410082)

在塔式太阳能发电系统中,定日镜群的布置方式常见的有按直线排列和按辐射排列2种，后者由美国休斯顿大学的 Lipps等[1]首先提出，它有利于减少阻挡损失。Pylkkanen提出了适用于辐射状布置方案的图形法，并给出了相关的数学公式。Siala等[2]则编制了相关的计算程序。定日镜设计要求能够在6级风作用下正常工作，在8级风作用下保证安全。Brosens[3]在1960年就开始研究阵风作用下刚性定日镜的振动问题；之后，Strickland等[4]利用风洞试验测试出近地面垂直于均匀来流的矩形平板背面的涡旋脱落频率；Stahl等[5]发现当定日镜与地面夹角小到一定程度时，气流撞击其表面产生的力将突然降低，在一些极限情况下，还可能产生升力；Bhumralkar等[6]将数值模拟手段运用到太阳能热发电设备的抗风研究中，利用二维数值模拟手段对加利福尼亚的1所100 MW太阳能热能发电站进行了模拟。随着新的试验技术和数值模拟技术的发展，目前对于太阳能反射装置抗风研究更加精细[7-9]。我国塔式太阳能发电还处于起步阶段，Wu等[10]分析了开缝情况下定日镜流场情况；卢春玲等[11]则考虑了支架影响，建立单体结构精细化模型进行计算。在实际使用中，定日镜通常以群的形式工作，处在群体中的定日镜流场受到相邻镜体的干扰，因此，有必要研究受到干扰后的定日镜流场分布。在一组塔式太阳能发电系统中，定日镜的尺寸统一，影响其相周围风环境的因素除了单体间的距离外，主要是其所处工况。在研究镜体间的相互干扰效应时，为了得到镜面风压的分布变化情况以及流场的整体面貌，本文作者利用 CFD方法计算模拟出定日镜前后布置的径向干扰，以及辐射状布置的径向与周向同时干扰等 2种形式，选取定日镜在正常工作、停放工况及最不利工况中有代表性的0°，60°和90°仰角下垂直迎风的情况进行分析。

1 计算原理

1.1 计算模型

本文使用标准k-ε模型(Standard k-ε Model)计算，该模型由Launder等[12]于1972年提出，是目前使用最为广泛的模型。它是在关于湍流动能k方程的基础上，引入湍动耗散率ε的方程，模型假设流动为完全湍流，分子粘性可以不考虑。标准k-ε模型计算量小，收敛速度快，计算结果与试验值较吻合，特别适用于绕流、边界层流动和有部分回流等工程实践问题，通常为首选模型。

1.2 参数定义

模拟中假定气流是不可压缩的定常流动。为了建造与风洞试验一致的流场，还需对入口风速和湍流度进行定义。

1.2.1 入口风速

计算参考工作点取为定日镜前端远处不受扰动的10 m高处，基本风速为8 m/s。与风洞试验一致，大气边界层风速剖面采用我国规范规定的指数风速剖面模拟，平均风速随高度z变化的表达式为：

其中：vz和v0分别为z高度和参考点高度处的平均风速；z0为计算高度及参考点高度；α为地面粗糙度指数，对于B类地貌，取0.16。

1.2.2 湍流强度

我国现行荷载规范没有明确湍流强度的定义，这里参考日本规范中的Ⅱ类地貌对B类地形的湍流强度进行模拟。

其中：Iu为湍流强度；z0取5 m；zG为梯度风高度，取350 m。

1.2.3 湍流动能和耗散率

入口处的湍流动能k和耗散率ε按以下公式计算：

其中：vz为入口处的平均风速；Iu为湍流强度；l为湍流积分尺度；Cμ为常量。对入口平均风速剖面、湍流强度剖面以及湍流积分尺度编制 UDF程序与 Fluent接口，以满足实际情况。

2 两定日镜径向干扰研究

2.1 网格划分

定日镜由于仰角的不同，其在水平面上的投影尺寸并不固定，可以用1个直径为其特征直径Dm的圆来表示它的工作空间。前、后布置的两定日镜位置关系如图1所示。其中：drj-1和drj-2分别为前、后定日镜编号；L和B分别为定日镜镜面部分的高和宽；Rm为径向间距，为2个定日镜立柱轴心间的距离。本文选择径向间距为18 m和36 m这2种布置进行计算。

图1 两定日镜模型布置方案Fig.1 Layouts of two heliostats mold

为了提高计算效率，同时保证计算速度，整个流域采用混合网格划分方式。在靠近定日镜结构的内部区域使用加密的四面体网格(Tetra Mesh)以适应复杂的边界情况，外部区域则采用较为稀疏的结构化六面体网格(Hexa Mesh)，两区域由内部面(Interior)分隔开，该面上划分结构化四边形面网格(Quad mesh)，以强制内部非结构化网格向外部结构化网格过渡，为了使非结构区域网格过渡均匀，这里使用 Gambit软件中的Size Function功能，设立渐变增长率为1.05。由于镜面非常薄，这里直接使用Face作为镜面模型，定日镜表面使用非结构化三角形面网格(Tri mesh)。计算域的选择原则及网格划分方法与单体部分的相同，都能够满足计算精度要求，图2所示为计算工况下两定日镜径向布置时的网格划分情况。

对于存在较多细小表面的结构，其网格质量的控制是难点[13]，这里使用混合网格划分方法后，可以较大程度地减少网格数量，对定日镜结构周围的区域进行细化，将更多的资源用于这些复杂结构中。在定日镜背部，立柱与横梁的交接处，最小划分尺寸为0.03 m，而在流域边界最稀疏的地方，网格尺寸达到2 m。不同工况下网格的数量有一定差异，以间距18 m、仰角为0°工况为例，其非加密区结构化网格为50万，而加密区域的非结构化网格达到196万，占总网格数的79.68%。当仰角为60°时加密区网格达到202万，占总网格数80.15%。对于定日镜这种外形特殊的钝体结构，利用混合网格后能够有效提高网格质量，各工况的最大网格倾斜度均低于 0.85，仰角为 60°时的网格质量相对更高；此外，使用Size Function功能严格控制网格尺寸的渐变比例不超过1.05。若全部使用非结构化网格，则在同等精度下，即使使用高性能计算机工作站也无法满足网格划分所需硬件条件。而在相同网格数下，网格倾斜度等指标超过0.95，不满足计算要求。

图2 两定日镜计算网格划分Fig.2 Calculation meshes of two heliostats mold

2.2 干扰因子

这里仅考虑顺风向静力风荷载的干扰效应，并使用干扰因子表达。Xie等[14]将干扰因子定义为：对于受到干扰作用下的建筑物，受扰建筑与无干扰情况下的建筑的顺风向静风力底部弯矩比。本文比较了受干扰与无干扰情况下，镜面的阻力系数 CD、升力系数CL以及绕立柱底部形心x方向的力矩系数CMx，分别计算了它们的干扰因子γ。干扰因子的计算公式为：

其中：Cdrj1和Cdrj2分别为drj-1和drj-2所对应的各个风力系数。将drj-1表面风压分布的数值模拟结果与文献[15]中同类型、同样风场下的单个定日镜表面风压的风洞试验数据进行对比，结果如图3所示。与文献[15]不同的是，这里仅选用了正面风压进行比较。通过比较发现：数值模拟结果与风洞试验结果一致；位于前方的定日镜drj-1受后方干扰非常小，可以将其作为未受干扰的结构进行计算。

图3 仰角为0°，60°和90°时镜面平均风压系数分布Fig.3 Mean wind pressure coefficient distributions of mirror when elevation angle is 0°, 60°and 90°

表1 Rm=18 m时的干扰因子Table 1 Interference factors when Rm=18 m

表2 Rm=36 m时的干扰因子Table 2 Interference factors when Rm=36 m

当径向距离为18 m和36 m时，前后布置的两定日镜在各仰角下的风力系数、力矩系数与干扰因子如表1和表2所示。表中阻力系数CD、升力系数CL、力矩系数CMx对应的干扰因子γ可分别表示为γD，γL和γMx。从表1和表2可以看出：对于前后径向布置的定日镜，无论是哪种工况，后方镜面的风压都严重地受到前方定日镜的干扰；且距离越近，干扰影响越明显，风力系数及力矩系数都减小得越多。对于仰角为0°时的工况，镜面主要以阻力为主，其径向间距Rm为18 m时，阻力干扰因子γD和弯矩干扰因子γMx都比较小，约为0.22和0.30；但在Rm达到36 m时，γD和γMx迅速增大，分别为0.82和0.83。在仰角为60°的工况下，Rm=18 m时的阻力、升力、力矩干扰因子都非常低，这与 Peterka 等[16]利用边界层风洞试验得到的结论相一致；随着距离的增大，当Rm=36 m时，各干扰因子虽然大幅度提高，但其值仍然不是很大，γD和γL为0.53，而γMx只有0.42。仰角为90°的情况更加特殊，其表面以升力为主，但升力系影响因子与力矩影响因子差异较大，不像前2种工况那样各干扰因子都比较一致。在Rm=18 m时，升力影响因子γL只有0.21，而弯矩影响因子γMx却达到0.76；当Rm=36 m以后，两者都有所提高，γL提高的幅度非常大，约为原来的3倍。

2.3 流场特性

2.3.1 仰角为0°时的流场特性

不同工况下的气流受前方扰动的机理差异很大，这也造成对后方镜面影响有较大差别。为了研究这种变化的差异，下面从受干扰后的定日镜风场特性方面进行讨论。

当仰角为 0°时，干扰流场分布图见图4。由图 4可见：在此工况下，镜面垂直于地面，气流绕过前端的drj-1，在镜面后侧上方及底部各卷起旋涡，尤其是上方旋涡尺度较大。

当Rm=18 m时，两镜面间的距离不足以为旋涡提供充分发展的空间，后方镜面阻塞了气流的流动，在2个镜面间产生回流，旋涡的结构受到破坏，被“挤压”在2个镜面间。drj-2的镜面压力由drj-1后方的涡旋产生，压力分布与未受干扰的情况差别非常大。气流沿涡旋脱落方向流动，在drj-2的顶部受到阻碍，沿镜面向下流动一段距离后，继续向内旋转，此时在镜面产生气流分离。因此，在drj-2的正面上可以看到上部有一个正压区，而下部大部分都处在负压区范围内。由于前方的气流方向改变，drj-2的底部没有气流流出，背面下部不再出现小的涡旋，而上部的涡旋尺寸也有所减小。drj-2背面的负压区最大位置在转动轴上侧，这与未受干扰时底部存在负压极值区不同。

当Rm=36 m时，drj-1的旋涡得到充分发展，drj-2处于drj-1的尾流区，此时气流已经基本恢复平行于来流方向流动，遇到drj-2后再次发生绕流、涡旋脱落等现象。从其流场分布图上可以看到前、后2个相似的流域。其表面压力与未受干扰的情况相类似，但由于drj-1背部对称的涡旋向相反的方向旋转，在中心产生低压区，所以，镜面最大压力对称分布在镜面上部两侧(图5)，背部也是底部负压最大。

2.3.2 仰角为60°时的流场特性

仰角60°工况的干扰效应流场剖面见图6。从图6可见：当气流遇到drj-1后，在迎风的前端分离，一部分顺镜面爬升，另一部分绕过镜面底部，形成涡旋；drj-1后方的气流受其影响很大，虽然没有在背部形成较大的涡旋，但流动方向发生变化，与地面产生一定的夹角，呈螺旋状向后方流动，随着距离的增大，该夹角逐渐减小，直至趋于平缓。

图4 仰角为0°时两定日镜流场分布图Fig.4 Flow distributions between two heliostats when elevation angle is 0°

图5 仰角0°时drj-2镜面平均风压系数分布Fig.5 Mean wind pressure coefficient distribution of drj-2 when elevation angle is 0°

图6 仰角为60°时两定日镜流场分布图Fig.6 Flow distributions between two heliostats when elevation angle is 60°

当Rm=18 m时，drj-2的来流受前方drj-1的干扰，由下向上倾斜流向drj-2。来流方向与镜面夹角大大减小，这样，drj-2的表面风压分布在来流一端产生剧烈梯度变化，并且由于气流仍有螺旋上升的趋势，在后方产生分离，镜面上存在较大面积的负压区域，但其值较小。与drj-1背面产生小的旋涡不同，drj-2整个镜面都处在螺旋状流动区域内，背部整体负压较大。

Rm=36 m时的情况与Rm=18 m时非常相似，只不过由于间距增大，气流趋于平缓，与地面的夹角更小。镜面风压分布以正压为主，来流一端的梯度变化没有前者剧烈。图7所示为60°工况下，drj-2的表面风压分布情况。

2.3.3 仰角为90°时的流场特性

在仰角为 90°时，气流遇到定日镜前缘向产生分离，但很快实现再附，然后，沿镜面继续向后方流动。迎风边缘由于柱状涡的存在，产生一个作用范围很小、梯度变化很大的负压区，可以看到drj-2的这个负压区与未受干扰的情况相比差别不大，而主要是柱状涡后大面积镜面上零散分布的正压区域有变化。这些正压影响到整个镜面的升力变化，而 90-000工况(即仰角为90°，风向角为0°)下本身的风压比较小，γL易受影响，变化较幅度较大，但由于正压基本上是沿转动轴对称分布的，对力矩影响不大。90-000工况的弯矩主要由作用在迎风一侧的负压决定，因此，弯矩干扰因子γMx始终保持较高值。当仰角为90°时，受干扰的定日镜表面风压分布见图8。

图7 仰角为60°时drj-2镜面平均风压系数分布Fig.7 Mean wind pressure coefficient distributions of drj-2 when elevation angle is 60°

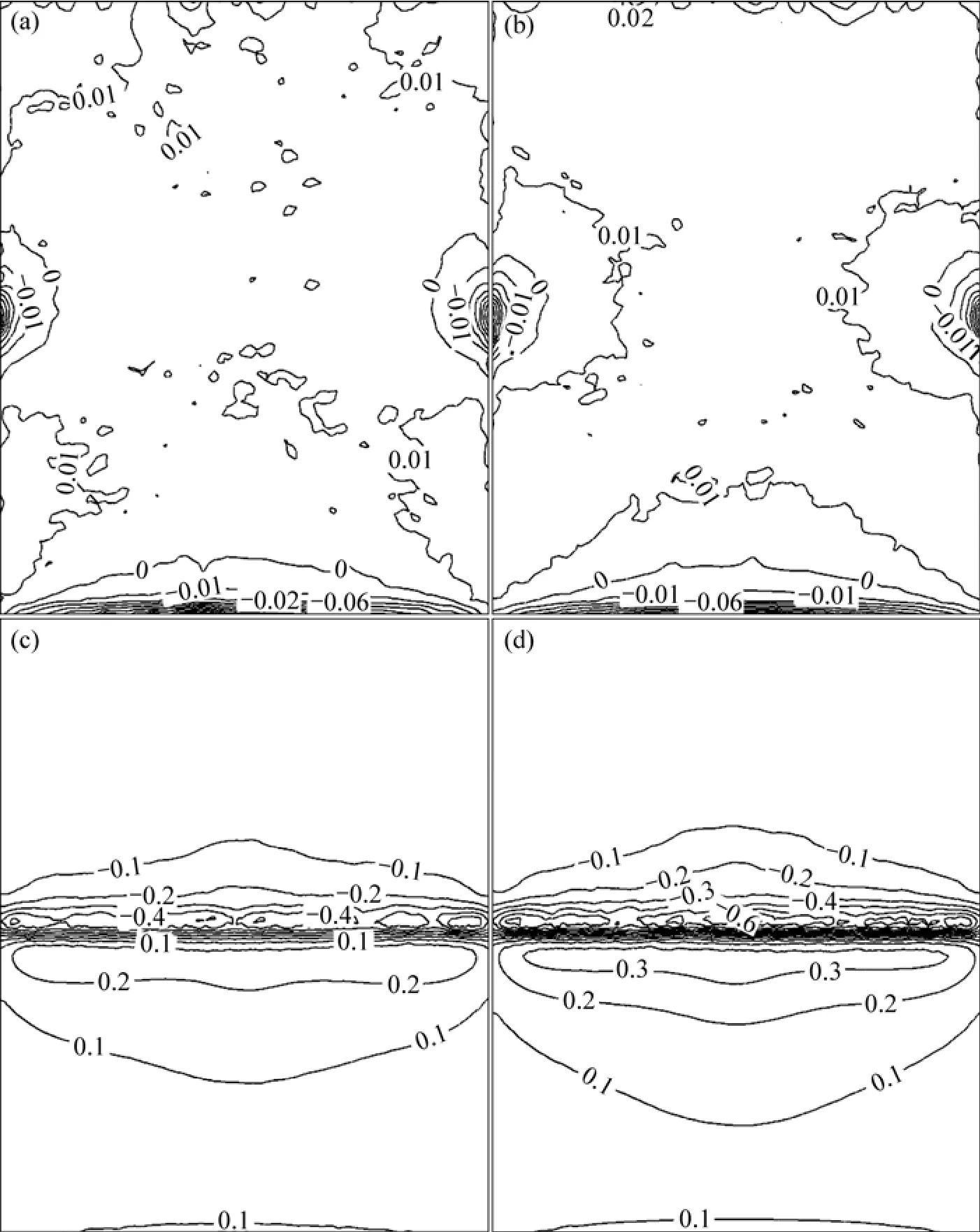
图8 仰角为90°时drj-2镜面平均风压系数分布Fig.8 Mean wind pressure coefficient distributions of drj-2 when elevation angle is 90°

3 四定日镜辐射状布置干扰研究

前面讨论了定日镜前后布置时风场的干扰效应及其成因，在实际使用过程中，定日镜场通常采用辐射状布置。本文选取有代表性的定日镜常用工作工况(仰角为60°)及休息工况(仰角为90°)作为研究对象，建立由4面定日镜构成、辐射状布置的模型，进行数值风洞计算。其中径向距离Rm=36 m，周向距离为32 m，模型布置如图9所示。图10所示为定日镜加密区网格。其中：drj-1，drj-2，drj-3和drj-4为定日镜编号。

以drj-1的各系数作为未受干扰的情况，计算其他各镜面的干扰因子，如表3所示。Randall等[17]针对槽式聚光镜系统进行风洞实验，研究单体及聚光器群在工作及休息状态下的风致力，发现在阵列中的反光镜受力大约是单体受力的 50%～65%。drj-2即为考虑前方正向和侧向定日镜影响的情况，其受干扰情况有类似反映，在工作工况下受干扰风力为未受干扰的57%～69%。

对于仰角60°的情况，在前、后径向布置的drj-1和drj-2之间增加了斜向布置的drj-3和drj-4后，drj-2的各干扰因子都有所增大，而drj-3和drj-4的各项干扰因子都大于1，这说明定日镜在辐射状布置的阵列中，会受到斜侧方结构的干扰，镜面压力有加强的趋势。进一步观察其速度流场分布图(见图11)可以看出：气流绕过drj-1后两侧气流的速度加大，向后方流动时受到drj-3和drj-4的阻碍，在其表面内侧产生的压力也增大。速度加强区域向后方沿一狭长区域分布，drj-2两侧的风压也有所加强。

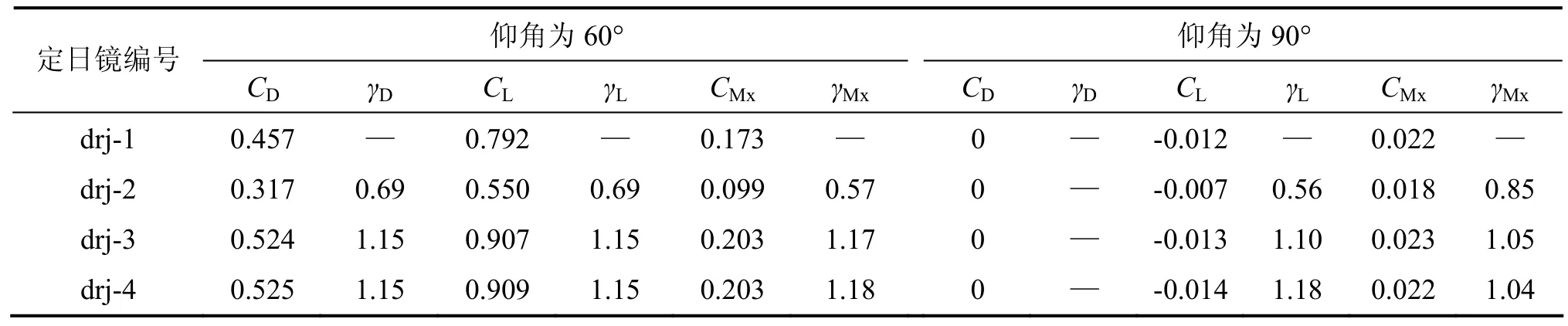
表3 辐射状布置干扰因子Table 3 Interference factors under radial disposition

图9 四定日镜模型布置方案Fig.9 Layout of four heliostats mold

图10 四定日镜网格加密区Fig.10 Local refined mesh of four heliostats mold

当仰角为 90°时，气流沿镜面流过，这种气流的加强并不明显，但受转动轴影响，也会在一定范围内影响后方镜面压力。可以预见：在布置有大量单体的定日镜场中，定日镜表面风压会受到斜侧方结构的影响而有所增大。这一点在定日镜结构抗风设计中应该注意。

图11 辐射状布置速度流场分布Fig.11 Velocity flow distributions under radial disposition

4 结论

(1) 利用数值模拟技术可以得到定日镜群表面风压和流场分布情况。通过合理地划分网格可大大减小计算工作量，提高计算精度，得到可靠的模拟结果。

(2) 在前、后径向布置的两定日镜中，当距离较小时，后方定日镜处于前方定日镜的尾流区，其表面风压受到严重干扰而大大减小。当仰角为0°时，对距离影响最为敏感，随着距离增大，干扰因子迅速增加。60°工况下，由于气流绕过drj-1后的方向发生很大改变，所以，在距离增大2倍时，干扰因子依然较低。

(3) 辐射状布置的定日镜受到斜侧前方定日镜干扰，表面风压呈现增长趋势，干扰因子大于 1，在设计时需要提高相应的风压计算值。

[1] Lipps F W, Vant-Hull L L. A cell-wise method for the optimization of large central receiver systems[J]. Solar Energy 1978, 20(6): 505-516.

[2] Siala F M F, Elayeb M E. Mathematical formulation of a graphical method for a no-blocking heliostat field layout[J].Renewable Energy 2001, 23(1): 77-92.

[3] Brosens P. Oscillations of a rigid heliostat mirror caused by fluctuating wind[J]. Solar Energy, 1960, 4(1): 49.

[4] Strickland J H, Matty R R, Barton G H. Vortex shedding from square plates perpendicular to a ground plane[J]. AIAA Journal,1980, 18(6): 715-716.

[5] Stahl W H, Mahmood M. Some aspects of the flow past a square flat plate at high angle of attack[J]. Developments in Mechanics,1985, 13: 481-482.

[6] Bhumralkar C M, Slemmons A J, Nitz K C. Numerical study of local regional atmospheric changes caused by a large solar central receiver power plant[J]. Journal of Applied Meteorology,1981, 20(6): 660-677.

[7] Naeenia N, Yaghoubi M. Analysis of wind flow around a parabolic collector (1) fluid flow[J]. Renewable Energy, 2007,32(11): 1898-1916.

[8] Naeenia N, Yaghoubi M. Analysis of wind flow around a parabolic collector (Ⅱ) heat transfer from receiver tube[J].Renewable Energy, 2007, 32(8): 1259-1272.

[9] WU Zhi-yong, WANG Zhi-feng. Numerical study of wind load on heliostat[J]. Progress in Computational Fluid Dynamics, 2008,8(7/8): 503-509.

[10] WU Zhi-yong, GONG Bo, WANG Zhi-feng, et al. An Experimental and Numerical Study of the Gap Effect on Wind Load on Heliostat[J]. Renewable Energy, 2010, 35(4): 797-806.

[11] 卢春玲, 李正农, 李秋胜. 风对定日镜影响的计算流体动力学数值模拟[J]. 自然灾害学报, 2010, 19(1): 185-191.LU Chun-ling, LI Zheng-nong, LI Qiu-sheng. Numerical simulation of wind effects on heliostat by computational fluid dynamics[J]. Chinese Journal of Natural Disasters, 2010, 19(1):185-191.

[12] Launder B E, Spalding D B. Lectures in mathematical models of turbulence[R]. London: Academic Press, 1972: 100-169.

[13] 谢华平, 何敏娟, 马人乐. 基于 CFD 模拟的格构塔平均风荷载分析[J]. 中南大学学报: 自然科学版, 2010, 41(5):1980-1986.XIE Hua-ping, HE Min-juan, MA Ren-le. Analyse of mean wind load of lattice tower based on CFD simulation[J]. Journal of Central South University: Science and Technology, 2010, 41(5):1980-1986.

[14] XIE Zhuang-ning , GU Ming. Mean interference effects among tall buildings[J]. Engineering Structures, 2004, 26(9):1173-1183.

[15] WANG Ying-ge, LI Zheng-nong, LI Qiu-sheng, et al. Wind pressure and wind induced vibration of heliostat[J]. Key Engineering Materials, 2009, 400/402: 935-940.

[16] Peterka J A, Bienkiewicz. B, Hosoya N, et al. Heliostat mean wind load reduction[J]. Energy, 1987, 12(3/4): 261-267.

[17] Randall D E, McBride D D, Tate R E. Parabolic trough solar collector wind loading[R]. San Francisco: American Society of Mechanical Engineers, 1980: 1-26.