考虑层间接触的沥青路面非线性疲劳损伤特性分析

孙志林，黄晓明

(1. 长沙理工大学 公路工程教育部重点实验室，湖南 长沙，410114；2. 东南大学 交通学院，江苏 南京，210096)

由于交通荷载作用，路面结构逐步疲劳损伤，结构特性发生改变，各结构层不再是匀质弹性体。从路面结构的疲劳损伤分析来看，目前通常采用损伤力学全解耦方法对路面结构在外荷载作用下的疲劳损伤过程与疲劳寿命进行研究，这种方法不能准确体现损伤与应力状态的相互耦合作用[1-5]。另一方面，在现行我国沥青路面设计规范路面结构设计方法中，假设道路各结构层之间为完全连续。施工中通过洒铺透层油和黏层油的方式尽量加强各层之间的连结能力。但是，由于各层材料之间的差异，想达到完全黏接的状态很难，特别是铺筑沥青面层之前，水稳性基层需要经过一段时间的养护，表面的灰尘清除不净对两层之间的连接影响较大。基于当前有关路面结构的疲劳损伤分析中没有考虑损伤与应力的耦合作用，以及实际路面结构层间不完全黏结这一情况[6-10]，为了更准确地反映路面结构疲劳损伤发展规律，本文作者运用损伤力学－有限元全耦合方法，分析层间结合状态对已损路面结构力学性能状态的影响。主要分析工具为ABAQUS有限元软件及用户材料子程序UMAT。

1 计算理论

1.1 疲劳损伤有限元方法

在疲劳损伤力学理论中，1个广泛应用的非线性损伤演化模型为 Chaboche模型，其损伤演化方程为[11]：

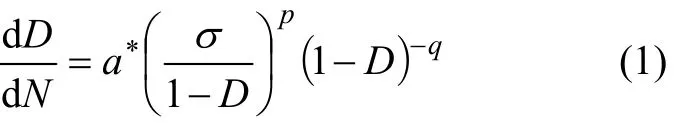
式中：D 为损伤度，在本研究中，取 0≤D≤0.5；N为荷载作用次数(疲劳寿命)；a*，p和q为材料的疲劳损伤特性参数；σ为拉伸应力。本文研究中采用此模型作为材料疲劳损伤分析模型。

本文中的有限元计算模型选择平面应变模型，此时，有限元方法的本构方程为：

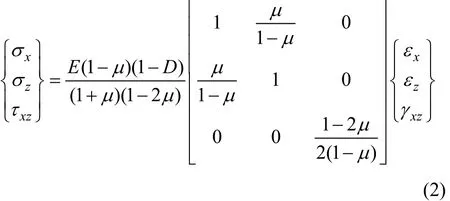
采用全耦合方法进行损伤力学有限元疲劳损伤累积分析，即每隔一定的应力循环次数对单元刚度矩阵进行重新计算，以反映疲劳损伤累积效应对单元刚度矩阵的影响。在有限元软件 ABAQUS提供的用户子程序接口上，采用 FORTRAN77编写用户子程序UMAT，以反映疲劳损伤对单元刚度的影响，采用耦合疲劳损伤的材料模型进行相应的编译连接，用于进行疲劳损伤分析。本文所用计算方法中，用户子程序UMAT中的单元刚度矩阵在每个增量步中都进行调用，每次调用之后按照疲劳损伤演化规律及时更新刚度矩阵中的疲劳损伤度D，因此，该方法属于全耦合解法，解法准确度要比全解耦和半耦合解法的高，具有明确的物理意义[12]。

1.2 层间接触有限元方法

ABAQUS软件采用*Contact Pair来模拟面面接触，可以考虑面与面间作用时的挤压、剪切以及相应方向的位移情况，同时还可模拟面与面间的脱开现象。ABAQUS面面接触以库仑摩擦理论为基础，用摩擦因数μ来表示接触面间摩擦行为。当接触剪应力等于或大于极限摩擦力μp时，接触面间出现滑动。由于模拟理想的摩擦行为较为困难，ABAQUS软件采用“弹性滑动”的罚摩擦公式来近似处理，自动选择罚刚度(图1中虚线斜率)。

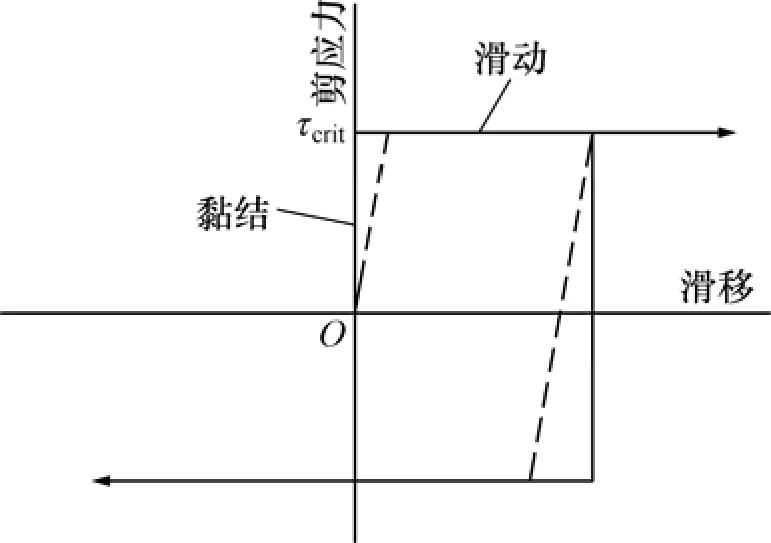
图1 库仑摩擦图Fig.1 Coulomb friction graph

为了保证计算精度及结果的收敛，进行以下处理：

(1) 考虑接触的 2个面采用相同的网络划分，结点尽量一一对应。

(2) 指定相互接触面时，模量大者作为主面，模量小者作为从面。

(3) 模式取小滑移。

2 结构计算模型

2.1 路面结构

采用我国目前常用的半刚性路面结构形式。路面结构各组成部分的材料如下：面层材料为沥青混凝土，基层材料为水泥稳定碎石，底基层材料为二灰土。各层材料的参数见表1。

表1 路面结构计算参数Table 1 Calculation parameters of pavement structure

有限元计算模型为平面应变模型，长×宽为 10 m×10 m。假定模型两侧与底部完全约束，路表为自由面，没有约束。靠近约束边界的位置各种力学响应很小，可忽略不计，故假定模型两侧与底部完全约束合理。结构计算模型如图2所示。

图2 结构计算模型Fig.2 Structure calculation model

本文中考虑面层与基层之间的不同连接状态时，其他层之间(基层与底基层、底基层与土基)以完全连续处理。另外，假设接触面在受力过程中竖向从不脱离，水平方向通过设定不同摩擦因数μ来传递剪应力。摩擦因数μ反映了层间的黏结状态，当摩擦因数为0时，表示完全光滑；摩擦因数越大，层间黏结越好。

2.2 材料疲劳损伤参数

张行等[11]在有关拉伸疲劳试验中，针对Chaboche提出的模型，得出：

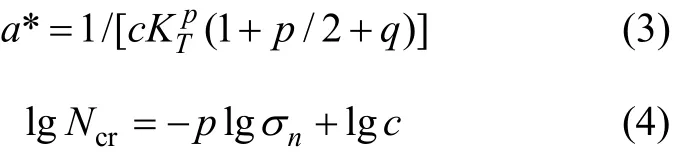
式中：a*，p，q和c为材料疲劳损伤特性参数；KT为应力集中系数，在本文中取 1；Ncr为裂缝形成疲劳寿命。

依据相关疲劳方程和试验数据[13-14]，可以得到 p和c，并取q=0，由式(3)可计算出a*。整理计算结果如表2所示。

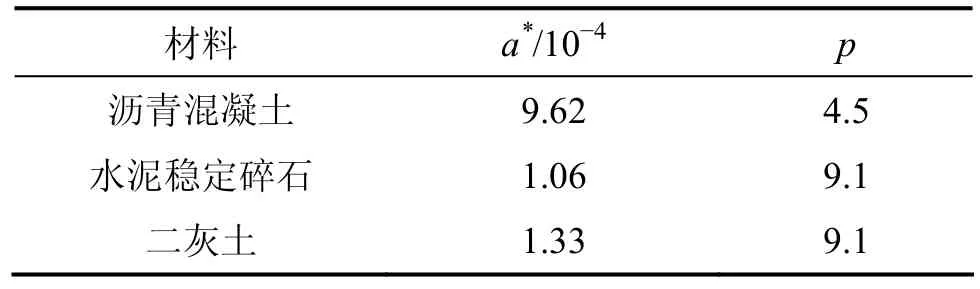
表2 Chaboche疲劳损伤模型参数Table 2 Chaboche fatigue damage model parameters

2.3 荷载条件

本文中，选取车辆荷载宽度W=156 mm，双轮中心距B=312 mm。选取荷载集度p=0.16 MPa，计算可得施加荷载为标准轴载，以保证各层结构的应力水平和路表弯沉在通常范围内，不影响路面结构力学响应的规律性分析。

3 计算结果与分析

3.1 损伤场分析

采用上述所给的路面结构计算模型，变化面层与基层之间的摩擦因数，分析荷载作用600万次后基层层底、底基层层底双轮中心线下损伤度的变化规律，如图3所示。

图3 面层与基层间摩擦因数μ对层底损伤度的影响Fig.3 Influence of friction coefficient between base layer and sub-base layer on damage degree of bottom layer

由图3可以看出：随着面层与基层层间摩擦因数的逐步增大，基层层底的损伤度缓慢增加，增加的幅度逐步增大；底基层层底的损伤度逐步减小，减小的幅度逐步减小；当接触系数达到10时，损伤度与完全连续时较接近；当面层与基层间摩擦因数很小时，基层与底基层的损伤度差别很大，随着摩擦因数的增大，两者的损伤度差别越来越小，直至基本相等。说明增大层间摩擦因数，保证层间良好的结合状态，能够充分发挥各层的承载能力。

3.2 应力场分析

改变面层与基层之间的接触状态，其他各层保持连续状态，分析荷载作用600万次后面层层底、基层层底、底基层层底水平正应力随摩擦因数的变化，如图4所示。

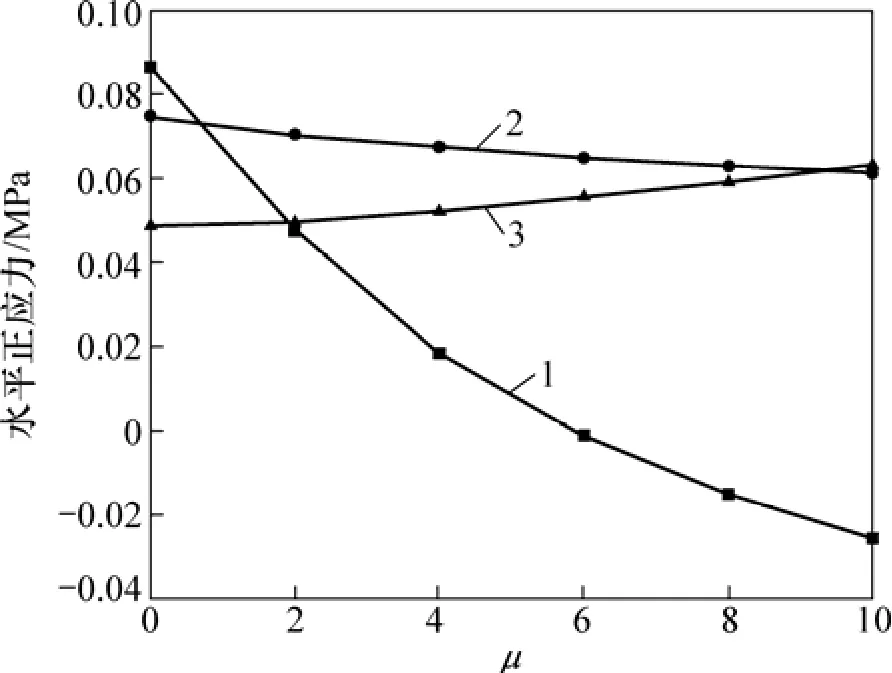
图4 面层与基层间摩擦因数对层底水平正应力的影响Fig.4 Influence of friction coefficient between base layer and sub-base layer on horizontal tensile stress of bottom layer

从图4可以看出：面层层底水平正应力随摩擦因数的变化趋势与通常无损路面[15]的变化趋势相同；当摩擦因数小于6.0时为拉应力，且随着摩擦因数的减小，拉应力逐渐增大；当摩擦因数大于6.0时为压应力，且随着摩擦因数的增大，压应力逐渐增大。基层与底基层层底水平正应力随摩擦因数的变化趋势与通常无损路面的变化趋势相反，随着摩擦因数的增大，基层层底的水平拉应力逐渐减小，而底基层则是逐渐增大。

与无损路面分析相比较，之所以会出现面层层底水平正应力变化规律不变而基层与底基层出现相反的规律，主要是由于面层层底大部分情况为压应力，此时面层底部不会出现损伤，因此，水平正应力的变化规律基本保持不变；而基层与底基层层底为拉应力，受拉应力损伤影响较大，应力分布规律会发生变化，所以会出现相反的规律。

3.3 路表弯沉分析

改变面层与基层之间的接触状态，其他各层保持连续状态，分析荷载作用600万次以后路表弯沉随摩擦因数变化的规律，如图5所示。

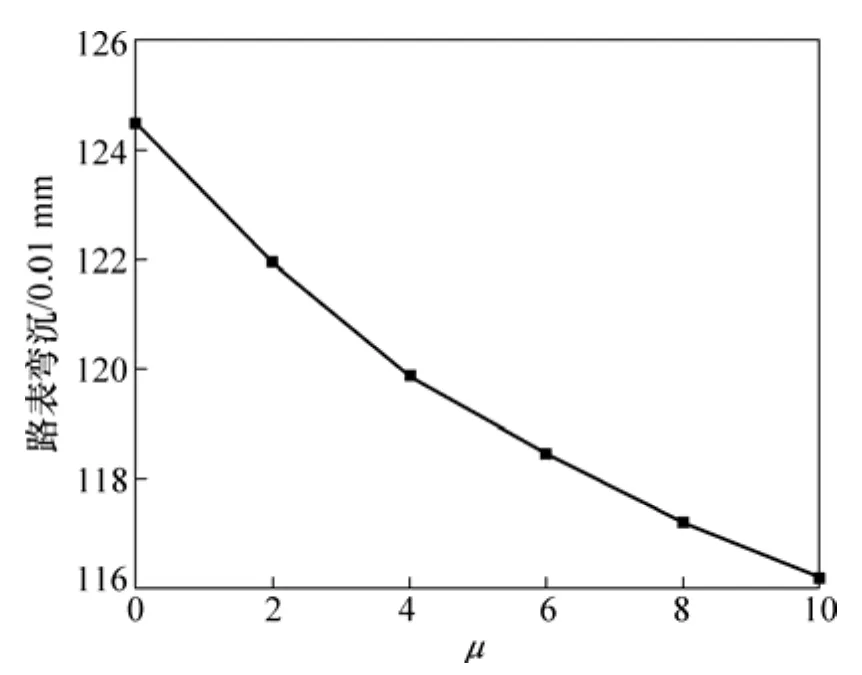
图5 面层与基层间摩擦因数对路表弯沉的影响Fig.5 Influence of friction coefficient between base layer and sub-base layer on deflection of surface pavement

由图5可看出：随着摩擦因数的增大，路表弯沉逐渐减小，且减小的幅度逐步减小。这与不考虑损伤[14]时的分析结果一致。由此可见：保持层间良好结合状态，有利于增强路面结构的整体承载能力。

3.4 裂纹形成疲劳寿命分析

改变面层与基层之间的接触状态，其他各层保持连续状态，分析基层与底基层裂纹形成疲劳寿命，如图6所示。

从图6可看出：随着面层与基层间摩擦因数增加，基层疲劳寿命减小，且减小幅度增加；底基层疲劳寿命增加，但增加幅度减小。这与前面所述的基层与底基层层底损伤度与层间摩擦因数的变化规律一致，这是因为路面结构疲劳寿命与路面结构疲劳损伤情况直接相关。

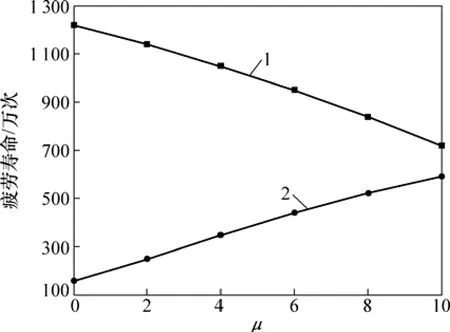
图6 面层与基层间摩擦因数对结构层疲劳寿命的影响Fig.6 Influence of friction coefficient between base layer and sub-base layer on fatigue life of structure layer

4 结论

(1) 基层与底基层、底基层与土基完全连续的条件下，随着面层与基层层间摩擦因数逐步增大，基层层底损伤度缓慢增加，增加幅度逐步增大；底基层层底损伤度逐步减小，减小幅度逐步减小；两者的损伤度差别越来越小，直至基本相等。这说明保证层间良好的结合状态，能够充分发挥各层的承载能力。

(2) 面层层底水平正应力随摩擦因数的变化规律与通常无损路面的变化规律相似。基层与底基层层底水平正应力随摩擦因数的变化规律与通常无损路面的变化规律相反，即随着摩擦因数的增大，基层层底的水平拉应力逐渐减小，而底基层则逐渐增大。

(3) 随着摩擦因数增大，路表弯沉逐渐减小，减小幅度逐步减小。因此，保持良好的层间结合状态，有利于增强路面结构的整体承载能力。

(4) 随着面层与基层间摩擦因数增加，基层疲劳寿命减小，减小幅度逐渐增大；底基层疲劳寿命增大，但增大幅度逐渐减小。

[1] 杨永顺, 王林, 高雪池, 等. 永久路面结构应变分布及疲劳损伤分析[J]. 山东大学学报: 工学版, 2009, 39(2): 118-124.YANG Yong-shun, WANG Lin, GAO Xue-chi, et al. Analysis of perpetual pavement strain distribution and fatigue damage[J].Journal of Shandong University: Engineering Science, 2009,39(2): 118-124.

[2] Castro M, Sanchez J A. Estimation of asphalt concrete fatigue curves: A damage theory approach[J]. Construction and Building Materials, 2008, 22(6): 1232-1238.

[3] SHU Xiang, HUANG Bao-shan, DRAGON V. Laboratory evaluation of fatigue characteristics of recycled asphalt mixture[J]. Construction and Building Materials, 2008, 22(7):1323-1330.

[4] 郑健龙, 吕松涛. 沥青混合料非线性疲劳损伤模型[J]. 中国公路学报, 2009, 22(5) : 21-28.ZHENG Jian-long, LU Song-tao. Nonlinear fatigue damage model for asphalt mixtures[J]. China Journal of Highway and Transport, 2009, 22(5): 21-28.

[5] SUO Zhi, WONG W G, LUO Xiao-hui, et al. Evaluation of fatigue crack behavior in asphalt concrete pavements with different polymer modifiers[J]. Construction and Building Materials, 2012, 7(1): 117-125.

[6] 艾长发, 邱延峻, 毛成, 等. 考虑层间状态的沥青路面温度与荷载耦合行为分析[J]. 土木工程学报, 2007, 40(12): 99-104.AI Chang-fa, QIU Yan-jun, MAO Cheng, et al. Simulation of the temperature and load coupling effect on asphalt pavement considering inter-layer conditions[J]. China Civil Engineering Journal, 2007, 40(12): 99-104.

[7] 白雪梅. 层间接触状态对沥青路面结构力学响应的影响[J].重庆交通大学学报: 自然科学版, 2009, 28(2): 215-218.BAI Xue-mei. Effect of bonding condition between asphalt layer and semi-rigid layer on structural mechanics response of asphalt pavement[J]. Journal of Chongqing Jiaotong University：Natural Science, 2009, 28(2): 215-218.

[8] 柳浩, 谭忆秋, 宋宪辉, 等. 沥青路面基-面层间结合状态对路面应力响应的影响分析[J]. 公路交通科技, 2009, 26(3): 1-6.LIU Hao, TAN Yi-qiu, SONG Xian-hui, et al. Influence of bonding condition between base and surface courses of asphalt pavement on pavement stress response[J]. Journal of Highway and Transportation Research and Development, 2009, 26(3):1-6.

[9] 李志宏, 黄宝涛. 沥青路面层间接触面积临界值的计算方法[J]. 建筑材料学报, 2008, 11(3): 311-317.LI Zhi-hong, HUANG Bao-tao. Calculation method for critical value of interlayer contact area of asphalt pavement[J]. Journal of Building Materials, 2008, 11(3): 311-317.

[10] 尹祖超, 钱振东. 全厚式沥青路面层间接触状态数值模拟[J].交通与计算机, 2008, 26(3): 119-122.YIN Zu-chao, QIAN Zhen-dong. Numerical simulation for interface contact condition of full-depth asphalt pavement[J].Transportation and Computer, 2008, 26(3): 119-122.

[11] 张行, 赵军. 金属构件应用疲劳损伤力学[M]. 北京: 国防工业出版社, 1998: 151-164.ZHANG Hang, ZHAO Jun. Application damage mechanics of hardware[M]. Beijing: National Defence Industry Press, 1998:151-164.

[12] 孙志林. 基于损伤力学的沥青路面疲劳损伤研究[D]. 南京:东南大学交通学院, 2008: 26-33.SUN Zhi-lin. Research on fatigue damage of asphalt pavement based on damage mechanics[D]. Nanjing: Southeast University.School of Transportation, 2008: 26-33.

[13] 孙荣山, 汪水银. 级配变化对水泥稳定碎石材料疲劳性能影响的研究[J]. 公路交通科技, 2007, 24(6): 57-61.SUN Rong-shan, WANG Shui-yin. Research on fatigue performance of the different gradation of cement stabilized crushed stone[J]. Journal of Highway and Transportation Research and Development, 2007, 24(6): 57-61.

[14] 谢军, 郭忠印. 沥青混合料疲劳响应模型试验研究[J]. 公路交通科技, 2007, 24(5): 21-25.XIE Jun, GUO Zhong-yin. Researching on fatigue model of asphalt mixtures[J]. Journal of Highway and Transportation Research and Development, 2007, 24(5): 21-25.

[15] 单景松. 行车荷载下路面结构响应分析[D]. 南京: 东南大学交通学院, 2007: 38-40.SHAN Jing-song. Analysis of pavement response under vehicle load[D]. Nanjing: Southeast University. School of Transportation,2007: 38-40.