基于非概率凸模型可靠性的结构优化设计
2012-06-22王晓军
王晓军 王 磊
贾 晓
(北京航空航天大学 航空科学与工程学院,北京100191)
(中国航空综合技术研究所,北京 100028)
邱志平
(北京航空航天大学 航空科学与工程学院,北京100191)
在实际工程优化设计中,由于制造、计算误差和外界干扰不可避免,不确定因素带来的问题也日益凸显.随着优化设计方法的更新及数值计算能力的加强,基于可靠性的优化设计理论成为研究的重点[1].
近几十年间,人们往往对基于概率可靠性的优化设计表现出更为浓厚的兴趣,在设计中要求系统元件失效的概率小于许用值,可以说概率可靠性理论在结构优化设计中取得了成功的应用[2].然而概率模型需要较多的信息数据,用来定义不确定参量的概率分布,常常缺乏结构样本的试验数据,无法满足概率可靠性模型的应用需求[3].同时,概率可靠性对参数极为敏感,微小的参数改变可能会导致最终分析结果大幅波动,这就说明在没有足够的数据信息以精确描述变量的随机性时,主观假设很大程度上导致计算结果的可信度下降.随着研究的深入,概率可靠性模型不再是最佳选择.
在许多情况下,虽然不确定变量(如载荷、几何尺寸、材料属性等)的概率分布情况不易准确描述,但是不确定参数的边界往往不难获得.基于这种思想,文献[4-5]从20世纪90年代开始提出了基于凸集合模型的非概率可靠性的概念,认为系统若能容许不确定参量的精确度在一定范围内波动,则系统是可靠的.并进一步将非概率可靠性界定为某一区间变量而非一具体值.其基本思想是:如果系统可以容许较大的不确定性而不失效,则系统视之可靠,反之系统是不可靠的.文献[6]将凸模型理论同结构的不确定优化设计相结合,通过叠加方法获取结构响应的极值,一定程度上减少了计算量.文献[7]提出以结构体积作为寻优目标,建立考虑位移非概率可靠性约束下三维连续体拓扑优化的数学模型,进而提出目标性能值的伴随法灵敏度分析算法.文献[8]提出了基于非概率凸模型的结构可靠性优化设计方法.文献[9-10]基于区间数理论,提出考虑区间变量的结构可靠性优化设计方法.文献[11]引用区间扰动方法,通过反优化技术处理不确定有界参数问题.文献[12]基于结构的应力-强度非概率区间干涉模型和可靠性分析模型,提出基于非概率集合可靠性的结构优化方法,通过指定可靠性指标作为约束条件,进行数值求解.
本文基于通过超椭球域界定不确定参量,将结构基本不确定变量安全域的超体积与其可行域的超椭球总体积之比作为结构非概率可靠性的度量[13-14],并赋值可靠度作为约束条件,利用拉格朗日乘子进行迭代求解,实现结构的可靠性优化.
1 不确定性变量的超椭球凸集模型
考虑结构在外载作用下的强度设计问题,由于结构的应力和强度往往受到多方面因素的影响,这些参数本身具有不确定性,所以结构应力和结构强度也是不确定的.
如果基于区间分析方法,将结构的不确定变量x通过一区间进行描述,令其上、下边界分别为xu,xl,则 x∈xI=[xl,xu]称为区间变量.令
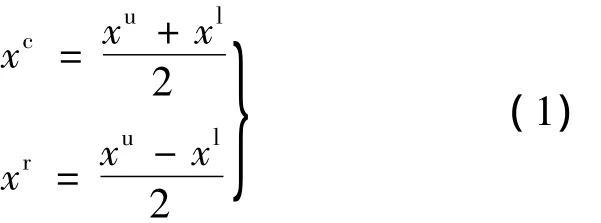
则有

其中,xc表征上述区间的平均水平,称为区间xI的均值;xr表征该区间相对于均值xc的波动情况,称为区间xI的半径.
文献[3]提出的用凸集模型来描述结构的不确定参量,即用超椭球表示不确定参量的取值范围,表示如下:
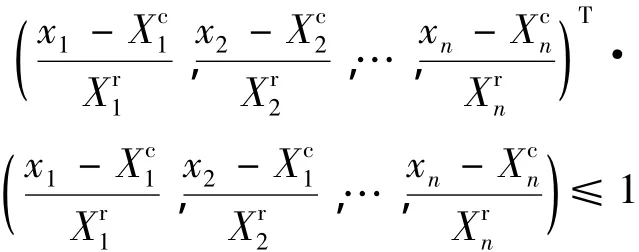
通过标准化参量转换,即令
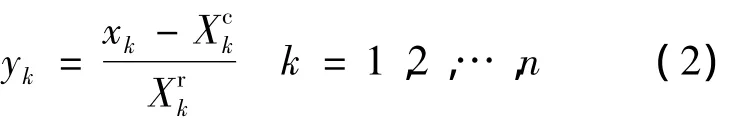
可将原凸集模型转换为一个等效的单位超球,变形如下:
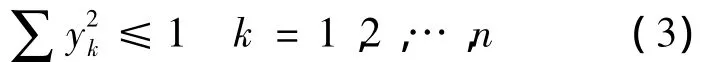
本文基于凸模型方法,将参数的不确定性量化在一个超椭球域内.通过标准化基本变量,进一步将变量的可行域(超椭球)归一化为一个等效的单位超球域.在标准化空间内,利用单位超球域与结构功能函数失效域之间的相互位置关系,实现对结构安全程度的度量.第2节将给出结构非概率凸模型可靠性指标的定义.
2 非概率可靠性度量
取结构功能函数为

这一线性形式,给定一组不同的S和R,判定结构所处的状态是安全还是失效,将不确定参量的取值空间分为安全域和失效域两部分,它们的区分界限称为极限状态平面,即
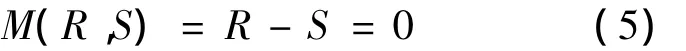
M的正值表示基本变量的安全集(安全域),M的负值表示基本变量的失效集(失效域),即
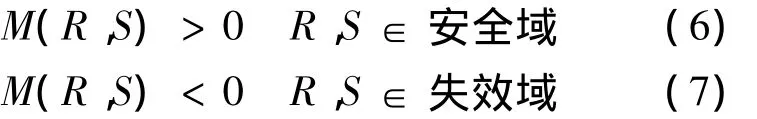
借鉴文献[15]提出的非概率集合可靠性理论,用单位超球与结构功能函数失效面之间的相互位置关系确定系统的安全程度,即定义非概率凸模型可靠性的度量指标.将取值空间中失效域与基本变量单位超球域之比定义为系统的失效度,简化至二维空间则表示为失效域面积与基本变量单位圆域面积之比,如图1所示.
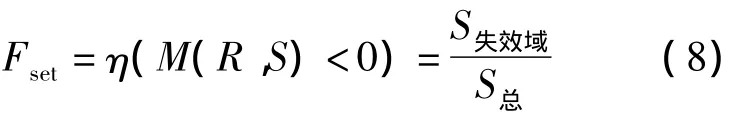
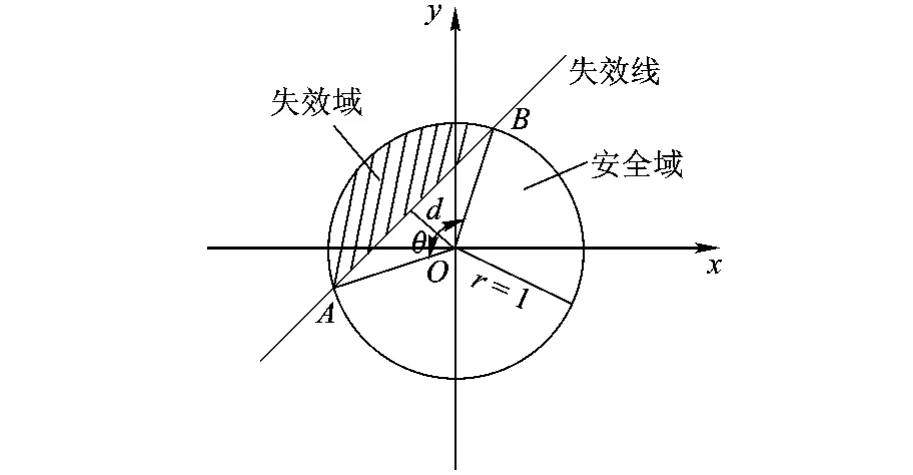
图1 基于非概率凸方法的可靠度计算示意图
与之对应,当结构的应力小于强度时,系统安全,定义取值空间中安全域面积与基本变量单位圆域面积之比为系统的可靠度,即
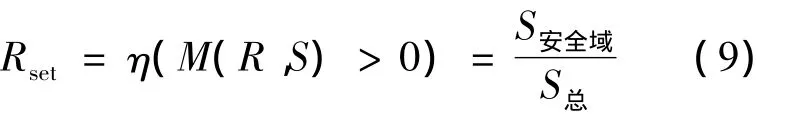
通过对非概率可靠性指标的度量,可以发现,给定不同的应力和强度集合,结构功能函数的失效面位置会发生变化,导致失效域和安全域的面积随之改变.根据图1与式(8)和式(9),非概率凸模型失效度和非概率凸模型可靠度可以表示为结构应力S和结构强度R的函数.具体计算公式如下:
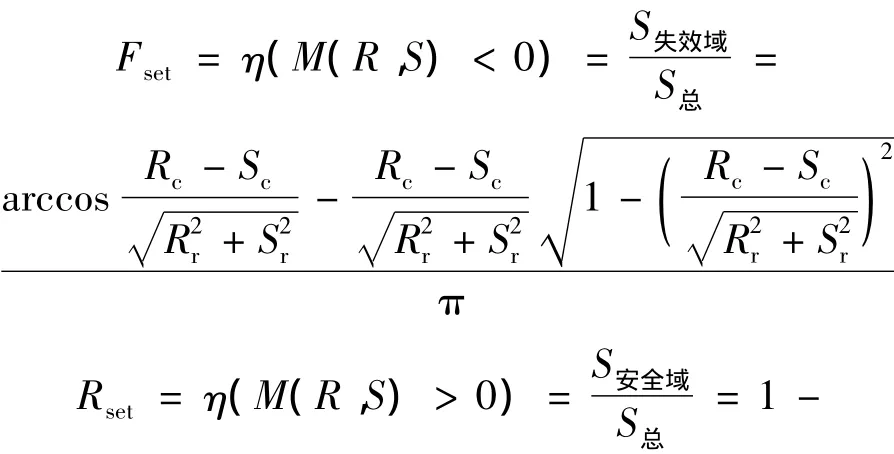
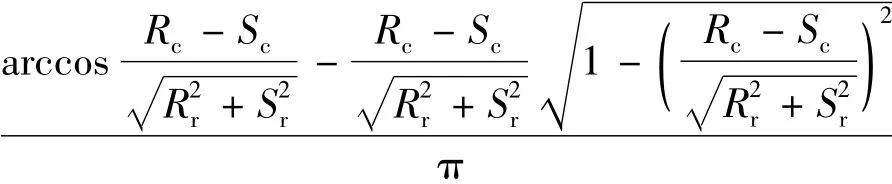
其中,Rc和Sc分别为强度和应力椭球中心;Rr和Sr分别为强度和应力椭球半轴.
3 结构非概率可靠性优化设计
3.1 优化设计模型
传统的结构确定性优化分析模型通常表示为
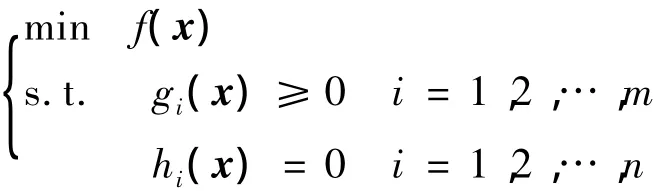
其中,f(x)是目标函数,x=(x1,x2,…,xn)T是向量形式的优化变量;gi(x)和hi(x)为约束条件;m和n是约束条件个数.
由于不确定性的影响,考虑可靠性,引入不确定变量和可靠性不等式约束条件.从而结构传统优化模型变形为如下结构非概率可靠性优化模型:
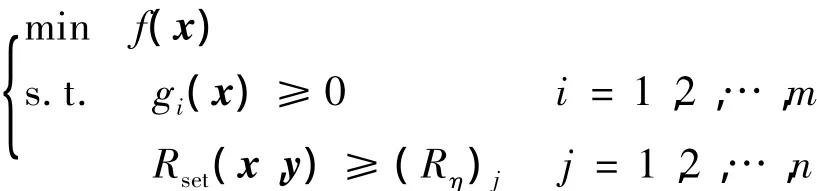
其中,y为不确定变量,可靠性约束条件表示为
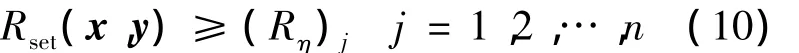
在第1节中已经提出,当把结构强度R和结构应力S表示为椭球变量时,结构的非概率凸模型失效度和可靠度表示为

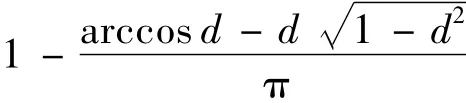
其中,d为原点到失效平面的距离.
针对结构设计要求,给定系统非概率失效度和可靠度的约束指标,使得系统每一个构件的非概率失效度都不大于给定值,非概率可靠度都不小于给定值,即

3.2 求解优化模型
由上文优化模型设计,通过Rockafellar乘子法和阻尼牛顿法对其进行迭代求解.针对不等式约束条件,首先引入松弛变量zi(i=1,2,…,m)和 zm+j(j=1,2,…,n),将问题转化为等式约束条件,优化模型变形为
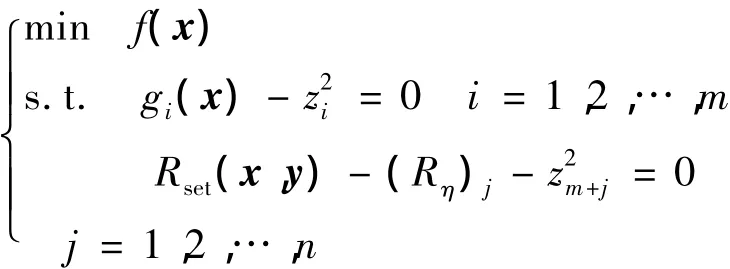
在等式约束条件下,引入相应的增广拉格朗日函数
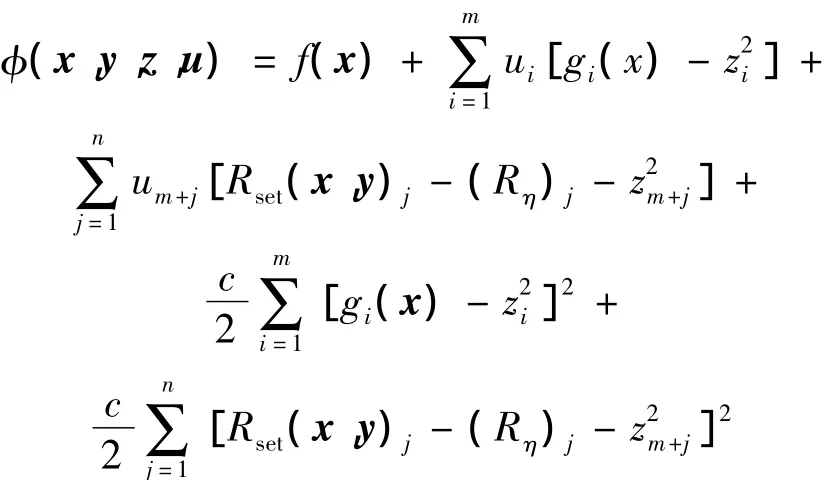
现在增广拉格朗日函数是一个四元函数,由于zi和zm+j是引入的松弛变量,要想求得最优化解,首先要使 φ(x,y,z,u)关于 z取极小值,即
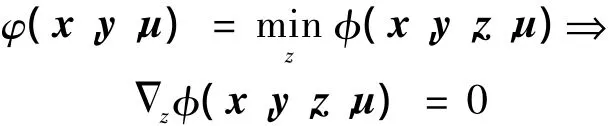
根据上式对z取偏导,可以得到
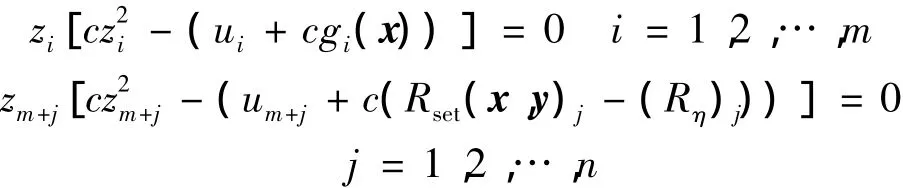
因此可以得到
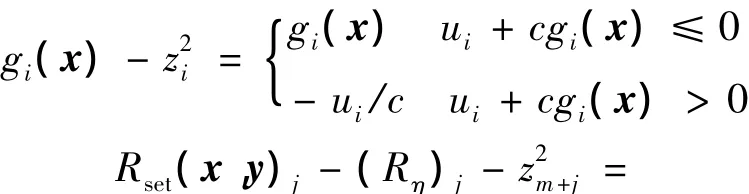
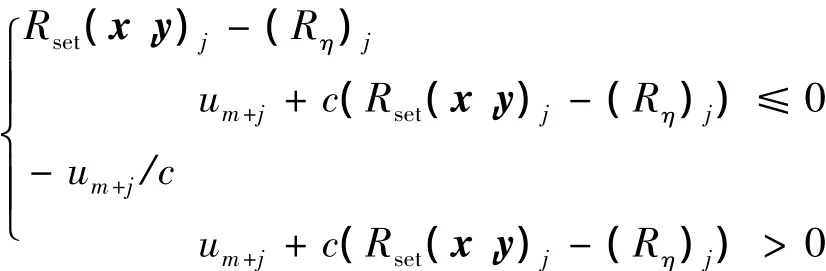
结合式(27)和式(28),增广拉格朗日函数最终变形表示为
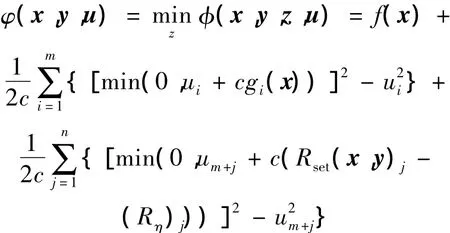
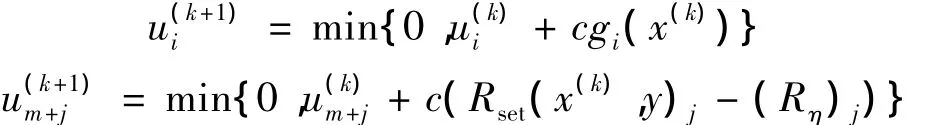
其中,上标k和k+1表示乘子u的迭代次数.
而结束准则可以表示为

其中,ε为允许误差.
通过乘子法,建立增广拉格朗日函数,对松弛变量z取极小值,将带约束的优化模型转化为无约束的优化问题,并采用阻尼牛顿法求解优化模型.其中,每步迭代沿方向为
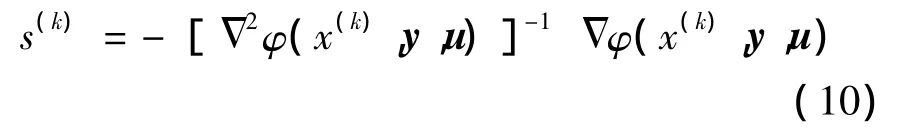
进行一维搜索来决定步长λk,即取λk,使
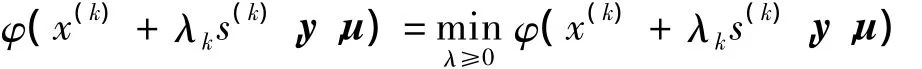
于是得到阻尼牛顿法的迭代公式为

相较于牛顿法对于步长总是赋值为1,阻尼牛顿法的步长选取更具有优越性,使得优化问题的收敛速度更快,并且对于初始点的选取条件较为宽松,在实际应用中取得了更好的效果.当然,阻尼牛顿法一定程度上增加了运算量,同时要求海赛矩阵 Δ2φ(x(k),y,u)的逆阵.而本文中目标函数是变量x的隐式函数,其导数不容易直接获得,应采用差分方法求得其近似解.
综上所述,基于非概率凸模型可靠性的结构优化设计问题,其求解步骤一般为
1)引入松弛变量将不等式约束问题转化为等式约束的优化问题;
2)将带约束的优化模型转化为无约束的优化问题;
3)给定初始点x(0),乘子向量的初始估计u(1),参数 c,允许误差 ε >0,k=1;
4)以x(k-1)为初始点,结合乘子法和阻尼牛顿法处理无约束的优化问题,即 min φ(x(k),y,u(k)),得解x(k);
5)若满足收敛准则,即计算式(10),迭代结束,得到近似解x(k)为最优解;否则,转到步骤4);
4 数值算例
本节里采用文献[4]中的算例,受压细杆在图2所示载荷作用下的屈曲失效问题.通过凸模型方法和区间分析方法来预测具有不确定初始几何缺陷细杆结构的动态屈曲响应集合.并根据Hoff判断准则,讨论以下两种判断准则下结构的稳定性问题.
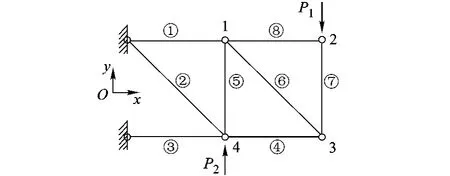
图2 八杆桁架示意图

分析图中桁架结构易知,外载作用下杆⑧为零力杆,所以只需对①~⑦杆进行优化问题的处理.通过数学运算得到各杆的应力区间.基于各杆应力区间和杆材料的抗拉、抗压区间,根据式(1)和式(3)可得用于计算各杆非概率凸模型可靠性的应力-强度椭球.
结合本文前述的基于结构可靠性指标的优化设计方法,此平面八杆桁架结构的非概率可靠性优化分析模型为
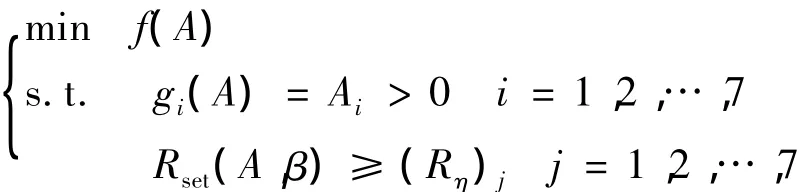
定义每根桁架杆处于安全状态时的非概率可靠度指标为99.9%,非概率凸模型可靠度的约束条件为

考虑到本文所述算例的约束条件(可靠性指标)与设计变量(截面积)之间存在着单调性的关系,进而使得目标函数的寻优简化为约束方程针对多变量的求解问题,无需考虑迭代即可获得不同外载作用下,桁架系统的最优化结果,见表1.
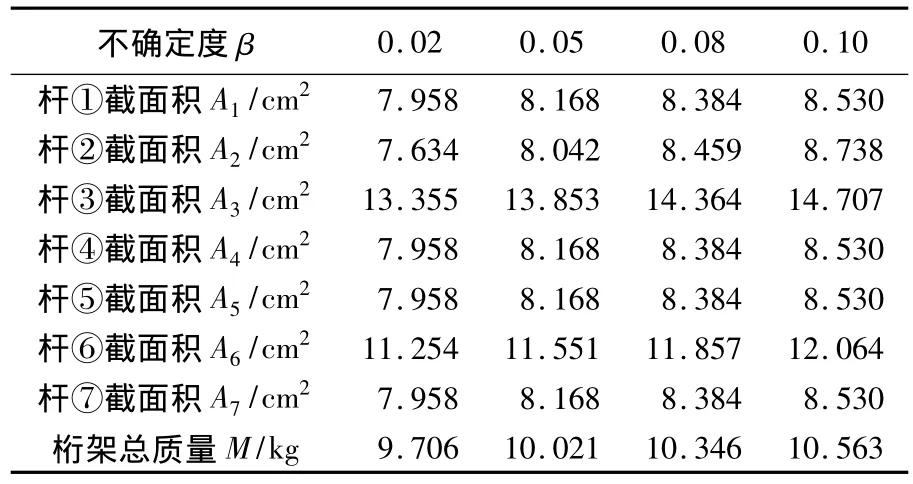
表1 不同外载PI作用下的优化结果
表1列出了每根杆的非概率可靠度的下限取99.9%时,各杆横截面积及总质量的最优化结果.对于此桁架系统,杆②、③和⑥所承受的力较大,所以最终的优化面积也比较大;杆①、④、⑤和⑦应力情况一致,得到的优化结果也相同.而且,随着外载分散度增大,优化横截面积也随之增大.
相较于文献[12]提出的基于区间变量的可靠性优化分析,与本文所述的基于凸模型的变量可靠性优化设计就不确定性的本质描述存在着明显不同.基于区间描述的不确定性在数学分析上不易用连续可微函数来处理,而往往只能采用图示的方法给予说明,且不易处理多变量问题;用凸模型来描述不确定变量则很好地解决了上述局限性,在可靠性分析以及基于可靠性的优化设计中体现出了更好的工程适用性.然而,若单单以优化结果来比较区间与凸模型两种方法,无法作出优劣性的评判,因为它们研究的内涵并不尽相同.
5 结论
基于区间描述的不确定性分析方法在数学处理上不易用连续可微函数来处理,因此使得非概率区间可靠性度量方法在实际应用中受到了一定的限制.本文基于凸模型方法,将影响结构的不确定参量表示为椭球变量,用结构安全域的体积与基本区间变量超球域的总体积之比作为结构非概率可靠性的度量,建立起新的非概率凸模型可靠性的结构优化模型.赋值可靠度作为约束条件,利用乘子法和阻尼牛顿法对优化模型进行数值计算,得到最优化解.本文中所述方法不需要获得不确定量的概率分布信息,只需知道其变化范围,对于实际问题的处理具有更为明确的物理意义和工程价值.本文提出的非概率可靠性优化模型清晰明了,不确定性变量集合和非概率凸模型可靠性指标连续可微,更易于处理多变量问题,从而使得基于凸模型的优化设计更为经济、合理,在工程上具有更好的实用性.
References)
[1]王光远.论不确定性结构力学的发展[J].力学进展,2002,32(2):205-211
Wang Guangyuan.On the development of uncertain structural mechanics[J].Advances in Mechanics,2002,32(2):205 - 211(in Chinese)
[2]Elishakoff I.Essay on uncertainties in elastic and vis-coelastic structures:from A M Freudenthal's criticisms to modern convex modeling[J].Computers and Structures,1995,56(6):871 -895
[3]Ben-Haim Y,Elishakoff I.Convex models of uncertainty in applied mechanics[M].Amsterdam:Elsevier Science Publisher,1990
[4]Ben-Haim Y.Robust reliability of structures[J].Advances in Applied Mechanics,1997,33:1 -41
[5]Elishakoff I.Discussion on:a non-probabilistic concept of reliability[J].Structural Safety,1995,17(3):195 -199
[6]Ganzerli S,Pantelides C P.Optimum structural design via convex model superposition[J].Computer Methods in Applied Mechanics and Engineering,2000,74(6):639 -647
[7]亢战,罗阳军.桁架结构非概率可靠性拓扑优化.计算力学学报,2008,25(5):589 -594
Kang Zhan,Luo Yangjun.Topology optimization of truss structures for non-probabilistic relisbility[J].Chinese Journal of Computational Mechanics,2008,25(5):589 -594(in Chinese)
[8]曹鸿钧,段宝岩.基于非概率可靠性的结构优化设计研究[J].应用力学学报,2005,22(3):381 -385
Cao Hongjun,Duan Baoyan.Approach to optimization of uncertain structures based on non-probabilistic reliability[J].Chinese Journal of Applied Mechanics,2005,22(3):381 -385(in Chinese)
[9]郭书祥,吕震宙.基于非概率模型的结构可靠性优化设计[J].计算力学学报,2002,19(2):198 -201
Guo Shuxiang,Lü Zhenzhou.Optimization of uncertain structures based on non-probabilistic reliability[J].Chinese Journal of Computational Mechanics,2002,19(2):198 - 201(in Chinese)
[10]程远胜,曾广武.结构非概率可靠性优化[J].华中科技大学学报,2002,30(3):30 -32
Cheng Yuansheng,Zeng Guangwu.Non-probabilistic reliability optimization of structures[J].J Huazhong Univ of Sci& Tech,2002,30(3):30 -32(in Chinese)
[11]Qiu Z P,Elishakoff I.Anti-optimization technique a generalization of interval analysis for nonprobabilistic treatment of uncertainty[J].Chaos,Solition & Fractals,2001,12(9):1747 -1759
[12]王晓军,杨海峰,邱志平,等.基于非概率集合可靠性的结构优化设计[J].计算力学学报,2011,28(6):827 -832
Wang Xiaojun,Yang Haifeng,Qiu Zhiping,et al.Structural optimization design based on nonprobabistlic set-theoretic reliability[J].Chinese Journal of Computational Mechanics,2011,28(6):827-832(in Chinese)
[13]Wang X J,Wang L,Elishakoff I,et al.Probability and convexity concepts are not antagonistic[J].Acta Mechanica,2011,219(1/2):45-64
[14]乔心州,仇原鹰,孔宪光.一种基于椭球凸集的结构非概率可靠性模型[J].工程力学,2009,26(11):203 -208
Qiao Xinzhou,Qiu Yuanying,Kong Xianguang.A non-probabilistic model of structural reliability based on ellipsoidal convex model[J].Engineering Mechanics,2009,26(11):203 - 208(in Chinese)
[15]Wang X J,Qiu Z P,Elishakoff I.Non-probabilistic set-model for structural safety measure[J].Acta Mechanica,2008,198:51 -64
