基于操纵面故障影响估计的安全飞行轨迹优化

李亦楠 杨凌宇 申功璋

(北京航空航天大学 自动化科学与电气工程学院，北京100191)

操纵面故障(例如失效、卡死、松浮等)是引起飞机事故的主要原因之一.故障的出现将改变飞机的动力学特性，缩小飞行包线.为了确保飞行安全、防止事故发生，需要规划安全飞行轨迹.如何分析故障飞机退化后的飞行性能，建立故障飞机模型，重新规划设计飞行轨迹以保证安全飞行/着陆，成为了当前国内外专家学者的研究热点之一.

针对上述问题，文献［1－2］将故障飞机模型抽象成平衡飞行状态点集合，认为飞行轨迹由配平轨迹序列组成.这种方式能够保证在每一轨迹片断内飞行满足包线范围和动力学约束，但还需要考虑相邻片断的连接问题，且一般适用于长距离轨迹规划.

文献［3－4］针对可重复使用运载器纵向质点模型，估计故障后的气动力以合理描述升降舵故障情况下的飞机运动情况，并采用最优控制的方法设计符合质点模型的安全着陆轨迹.这种方法在规划过程中考虑了故障飞机动力学约束、各状态量和控制量约束，能够同时计算得到符合故障模型的最优飞行轨迹和与该轨迹对应的速度及各控制量、状态量随时间的变化规律，以作为内环姿态控制器的控制指令.

基于文献［4］，本文估计横侧向操纵面故障对飞机的影响，以控制量变化率最小为优化指标，给出轨迹优化问题的描述，并采用高斯伪谱法求解该最优控制问题，将安全飞行轨迹优化推广到三维空间.

在众多数值优化方法［5］中，高斯伪谱法由于其以全局插值多项式为基函数，具有较高的精度而被认为最具工程应用价值［6］，并且它在优化效果和收敛性方面优于现有其他伪谱法.最后的数值仿真给出了在副翼和方向舵故障两种情况下的优化设计结果.

1 操纵面故障时安全轨迹优化问题

1.1 操纵面故障飞机质心运动方程

根据文献［7］推导，可得航迹坐标系下完整的质点运动方程:

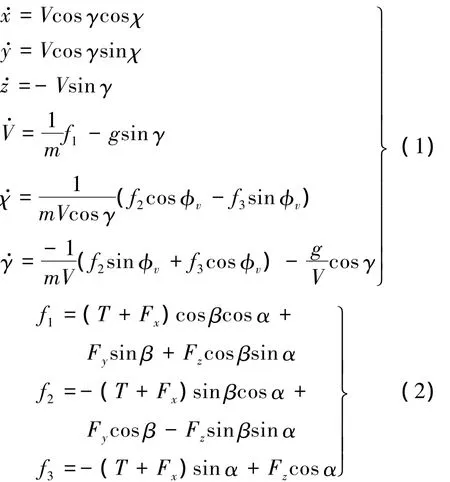
式中，x，y，z分别为飞机在惯性坐标系下的3个坐标分量;V，χ，γ分别为飞行速度、航向角和航迹倾角;m和g分别为飞机质量和重力加速度;α为迎角;β为侧滑角;φv为速度滚转角;T为沿机体x轴的发动机推力;Fx，Fy，Fz分别为气动力在机体轴3个方向上的分量;f1，f2，f3分别为推力和气动力的合力在气流系下的分量.忽略角加速度相关项，可得

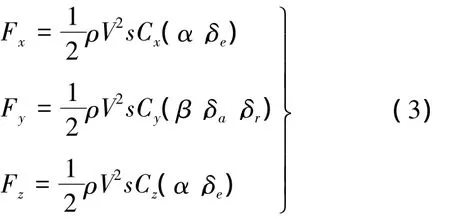
式中，ρ为空气密度;0.5ρV2为动压;s为机翼参考面积;δe，δa，δr分别为升降舵、副翼和方向舵偏转角;p，q，r分别为滚转、俯仰和偏航角速度;Cx，Cy，Cz分别为沿机体轴 x，y，z方向的气动力系数.

正常飞机模型一般忽略侧滑角β和侧力Fy，但当横侧向操纵面发生故障时，为平衡由故障引起的干扰力/力矩，β和Fy将不再保持为0.由于操纵面卡死引入的干扰往往为常值，且不同平衡飞行状态下的侧滑角也基本相同，为缩短优化时间，认为在轨迹优化过程中β保持为固定值β*，Fy通过β*计算得到，即

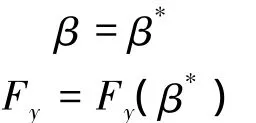
因此，为描述操纵面故障情况下的飞机运动模型，除由式(1)～式(3)表示的质点模型外，还需要估计操纵面故障的影响，即分析计算由故障产生的配平值β*和对应的Fy(β*).

1.2 优化问题描述

一般地，初始和终止飞行状态均为平衡飞行状态，相应的推力、气流角和姿态角需满足配平飞行条件.为方便设置两端状态条件，在前述质点模型基础上增广方程［8］:

式中，RT，Rα，Rφv分别为推力、迎角和速度滚转角的变化率，并将其作为增广系统的控制量U=［RTRαRφv］T，同时扩展形成新状态量 X=［x y z V χ γ T α φv］T.

操纵面故障将直接影响飞机的转动运动，导致气流角和姿态角变化减慢，U受较大限制.本文取U的二次型表达式为代价函数进行惩罚.则操纵面故障飞机的轨迹优化问题可描述如下.

寻找控制量U(t)和相应的状态量X(t)，使在时间［t0，tf］内，有

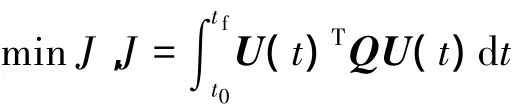
s.t.质点运动模型约束:

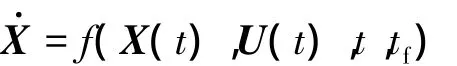
两端状态约束:

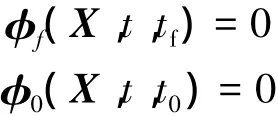
控制和状态量约束:

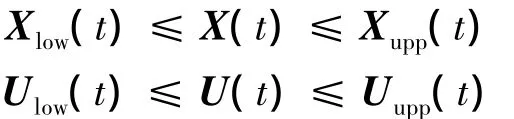
式中，矩阵Q为加权矩阵;φ0(·)和φf(·)分别为初、末状态约束函数;下标low和upp分别表示下限和上限.

2 操纵面故障影响估计

2.1 计算方法

飞机的转动运动总是远远先于平动运动达到平衡.根据文献［3］，以转动运动平衡或转动角加速度最小为目的进行操纵面故障后的气动力系数计算.当某一操纵面发生故障而对模型产生干扰时，其余操纵面需要偏转特定的角度以产生平衡力矩，这将改变飞机的平衡状态和气动力系数.为尽可能平衡转动运动，需要在允许范围内寻找最佳操纵面配置使合外力矩最小，即

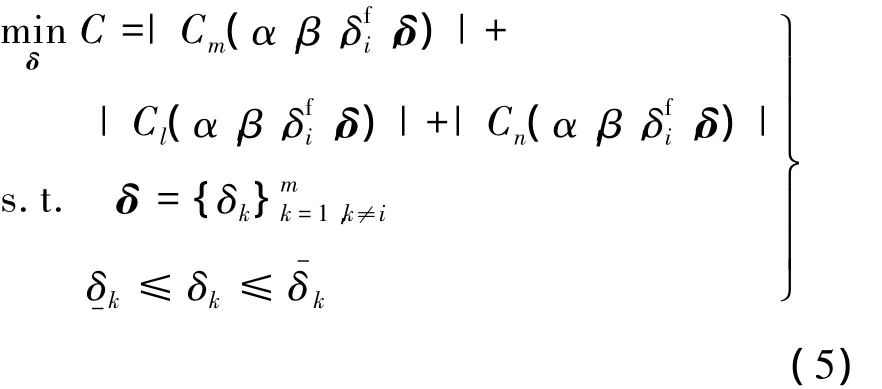
式中，Cm，Cl，Cn分别为俯仰、滚转和偏航力矩系数为故障操纵面;δ 为其余操纵面向量;δ－k和分别为第k个可用操纵面偏角的下限和上限;m为操纵面总个数.

求解上述优化问题，得到其余操纵面最佳配置δ*，并重新计算受操纵面故障影响的气动力系数:

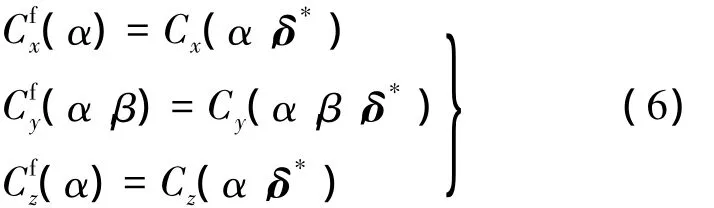
式中，上标f表示操纵面故障后的结果;上标*表示最佳配置结果.

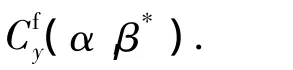
2.2 操纵面故障影响分析算例

现分析某型飞机横侧向操纵面卡死的情况.δa是产生滚转力矩的关键操纵面，10°以内非零位置的卡死足以影响飞机的配值，10°以上的卡死将导致飞机无法稳定飞行;δr虽然对配平影响较小，但却是产生侧滑和侧力的关键因素.由气动系数表达式［9］可知，δa和 δr只影响 Cy.令 3 个气动力系数的角速度分量为0，忽略δr对纵向气动力的影响并简化拟合阶数，可得

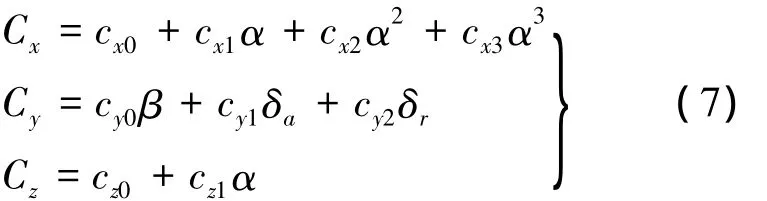
式中，cx0～cz1分别为拟合系数.

由于δa或δr故障对纵向影响很小，可省去Cm一项，则式(5)的优化指标部分可改写为

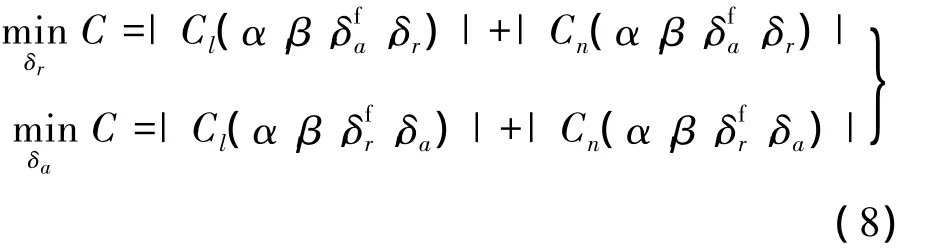
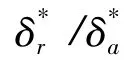
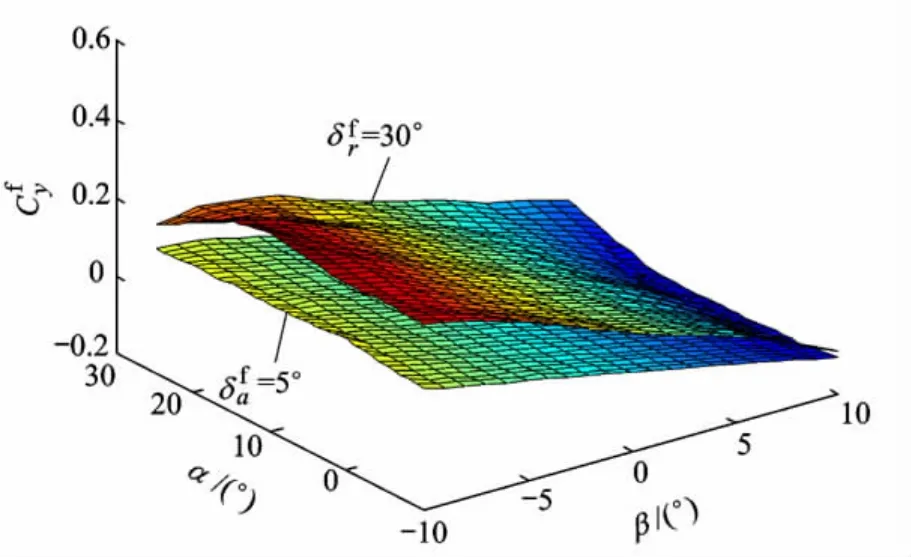
图1 δa卡死在5°和 δr卡死在30°时的

由图1可知，故障使侧力系数非零.尤其当δr卡死在30°时，为保证转动平衡，为较大的正值，影响大于δa卡死在5°的情况.另外，根据随α和β的变化情况，β是影响系数值的主要因素，且存在近似的线性关系，如图2所示.

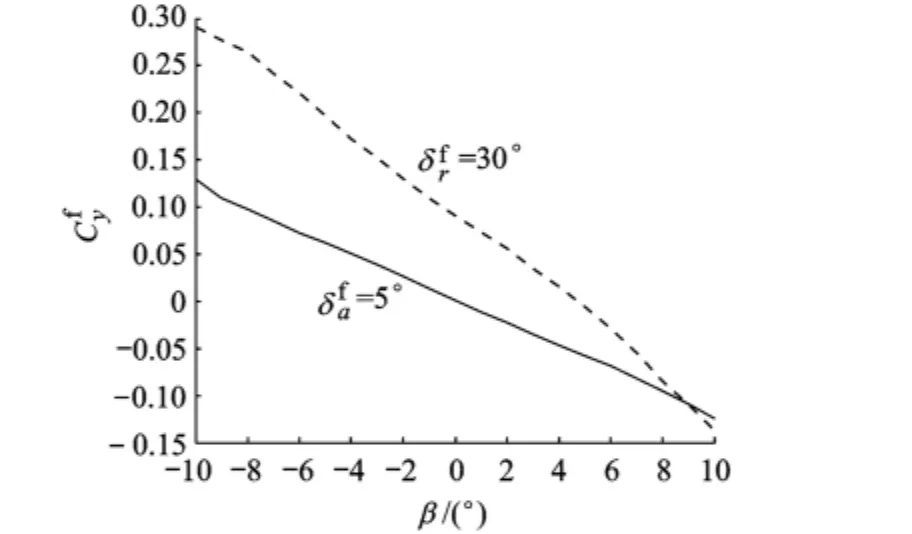
图2 两种故障情况下固定α，随β的变化情况

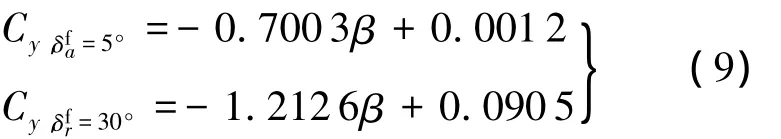
除此之外，表1给出了δr卡死在其他不同角度时的拟合结果.而δa对侧力的影响相对较小，不同卡死角度下的侧力相差并不大.

表1 不同卡死情况下的侧力系数

综上，结合式(1)～式(4)和式(9)，即可得到完整的操纵面故障飞机模型.

3 高斯伪谱法的计算过程

本文针对上述分析得到的操纵面故障飞机质点模型，采用高斯伪谱法［10］设计飞行轨迹.

用Lagrange多项式离散化连续系统状态量X(t)和控制量 U(t)为 X(tk)和 U(tk).采用Gauss型求积法计算动力学积分项.将时间区间［t0，tf］投影到区间(－1，1)内，并用 N 阶 Legendre多项式零点作为求积节点tk(k=0～N)，则可将原最优控制问题转化为非线性规划问题，即

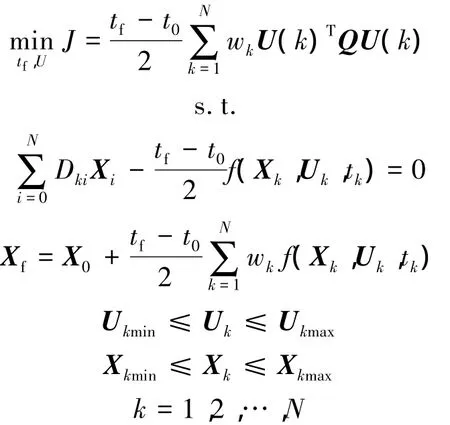
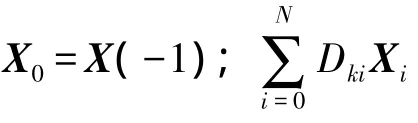
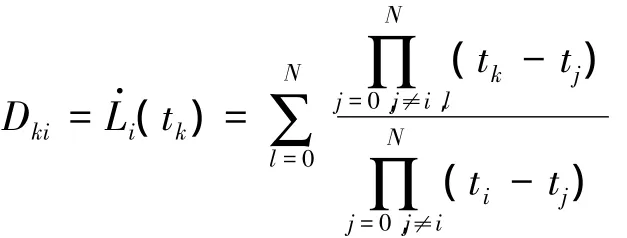
然后，用数值优化方法求解该非线性规划问题，这里采用序列二次规划方法.

4 数值仿真

针对2.2节中飞机模型，分别在操纵面正常、δa卡死在5°和δr卡死在30°3种情况下优化安全飞行轨迹.给定初始状态为

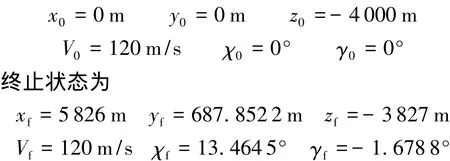
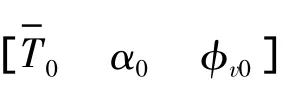
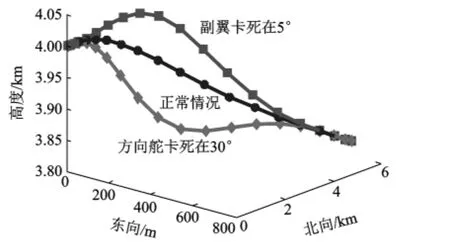
图3 3种故障情况下三维空间最优轨迹

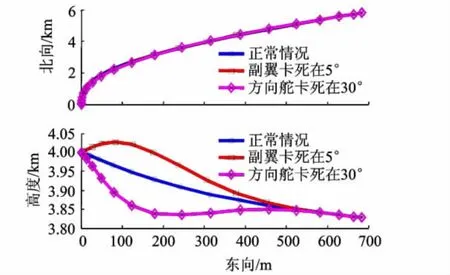
图4 3种故障情况下最优轨迹的横向和纵向剖面

3种情况下，优化结果均满足了两端位置和端点平衡状态的约束，实现了三维空间位置的转移和初、末状态的过渡.3条轨迹对应的控制量随时间的变化如图5所示，α变化率均在10－2(°)/s以内，φv变化率不超过 0.6(°)/s.各量随时间变化均较为缓慢，从而保证平滑飞行.

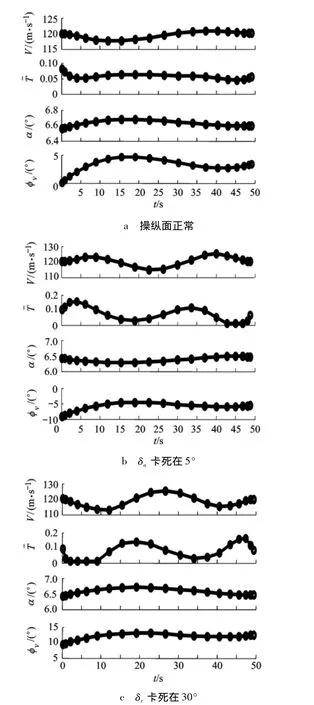
图5 3种情况下的速度和控制量时间曲线

分析图4和图5的优化结果，整个飞行过程中，α和φv变化缓慢，而推力相对频繁地调节以实现飞行状态过渡，这也因此直接影响了飞行速度时间曲线的变化和空间轨迹高度的变化.

5 结论

本文的研究目的是在操纵面发生故障时，优化设计三维安全飞行轨迹.建立了操纵面故障情况下的飞机模型，在正常飞机模型的基础上引入侧滑和侧力项并计算了受故障影响的气动力系数，更精确地反映了故障飞机的运动特点.结合安全飞行的需求，考虑下降的机动性能和控制能力，扩展了原动力学模型并以控制量变化率最小作为优化指标，采用高斯伪谱法进行设计.仿真结果表明，所得的三维飞行轨迹符合动力学方程约束，满足了飞行状态量和空间位置的平缓过渡，能够保证飞机在故障情况下安全飞行.

References)

［1］Atkins E.Dynamic waypoint generation given reduced flight performance［R］.AIAA-2004-779，2004

［2］Strube M J.Post-failure trajectory planning from feasible trim state sequences［D］.College Park:Dept of Aerospace Engineering，University ofMaryland at College Park，2005

［3］Oppenheimer M W，Doman D B，Bolender M A.A method for estimating control failure effects for aerodynamic vehicle trajectory retargeting［R］.AIAA-2004-5169，2004

［4］Fahroo F，Doman D.A direct method for approach and landing trajectory reshaping with failure effect estimation［R］.AIAA-2004-4772，2004

［5］Betts J T.Survey of numerical methods for trajectory optimization［J］.Journal of Guidance，Control and Dynamics，1998，21(2):193－206

［6］雍恩米，陈磊，唐国金.飞行器轨迹优化数值方法综述［J］.宇航学报，2008，29(2):397－406

Yong Enmi，Chen Lei，Tang Guojin.A survey of numerical methods for trajectory optimization of spacecraft［J］.Journal of Astronautics，2008，29(2):397－406(in Chinese)

［7］肖业伦.航空航天器运动的建模［M］.北京:北京航空航天大学出版社，2003:18－37

Xiao Yelun.Modeling of aircraft and spacecraft motion［M］.Beijing:Beijing University of Aeronautics and Astronautics Press，2003:18－37(in Chinese)

［8］Yakimenko O A，Xu Y，Basset G.Computing short-time aircraft maneuvers using direct methods［R］.AIAA-2008-6632，2008

［9］Morelli E A.Global nonlinear aerodynamic modeling using multivariate orthogonal functions ［J］.Journal of Aircraft，1995，32(2):270－277

［10］Benson D A，Huntington G T，Thorvaldsen T P，et al.Direct trajectory optimization and costate estimation via an orthogonal collocation method［R］.AIAA-2006-6358，2006