航天器交会远程快速自主制导方法

赵书阁 陈 统 徐世杰

(北京航空航天大学 宇航学院，北京100191)

航天器交会对接通常需要经历远程调相接近段、近程相对导引段、终端接近段、对接段等过程［1］.远程调相接近段是指追踪航天器与目标航天器的距离大于几十或十几公里，跟瞄设备还无法捕获目标之前接近操作.在这个阶段，追踪航天器可以通过地面测控站进行导引控制，为提高轨道机动的可靠性，一般要求航天器的轨道机动限定在地面测控站的范围内［2］.但是为了减少操作的复杂性，降低任务的费用，简化航天器的地面支持系统，缩短远程导引时间，自主化的远程调相接近技术也越来越受重视.

基于Lambert问题的最优轨道转移方法是航天器交会远程接近操作的主要方法［3－6］.但是这种方法通常计算量较大，不利于在轨自主实时运算;而且该方法是一种开环控制方法，如果不设计中途修正，会造成很大的导引偏差.另一种远程接近方法是基于C-W方程的最优多脉冲转移方法［7－8］，但是该方法也存在在轨自主实时解算困难、无法实现闭环控制的缺点，而且C-W方程的线性化误差会随着距离的增大而增大，不利于远程导引.

对于轨道要素相差较小的两航天器的远距离接近，文献［9］通过半长轴调整和时间累积效应协调的方式，实现对目标3个方向的接近，节省了控制所需燃料，但整个轨控过程需要在50 d内完成，快速性差.本文针对远程导引变轨任务，以经典轨道要素作为轨控参数，基于特殊点变轨设计了自主接近流程，以获得满足约束指标的轨控参数，完成远程段快速接近.

1 经典轨道要素变轨的基本模型

1.1 特殊点变轨原理

特殊点变轨的实质是利用轨道动力学特性，将轨道面内外的调整分开，减小相互耦合性，便于轨控参数的计算.根据Gauss摄动运动方程体现的轨道动力学特性，给出应用于本文的特殊点变轨原理:

1)由于轨道半长轴决定轨道周期，因此在轨道平面内，可以利用两个航天器的半长轴偏差调整两航天器的纬度幅角差.半长轴的调整是利用一次近地点和远地点的双脉冲实现.对于小偏心率的近圆轨道，为了在半长轴调整过程中避免轨道的近地点和远地点发生互换，规定轨道抬高首先在近地点开始执行，轨道降低首先在远地点开始执行.轨道偏心率的调整可以通过调整近地点和远地点高度间接实现.

2)在远地点(近地点)施加径向推力时，不改变半长轴(轨道高度)及偏心率，只改变近地点幅角，可以用来修正近地点幅角偏差.

3)在升交点或降交点施加法向冲量，可以调整轨道倾角而对升交点赤经影响很小;当纬度幅角u=π/2或3π/2时施加法向冲量可以调整升交点赤经而对轨道倾角影响很小;当 u=arctan［ΔΩsin(i)/Δi］时，一个法向冲量可以同时调整轨道倾角和升交点赤经.

1.2 速度增量与轨道要素变化关系

设施加在轨道横向、法向和径向上的瞬时速度增量分别为Δvu，Δvh和Δvr，根据Gauss摄动方程［10］，半长轴的变化量与横向速度增量以及近地点幅角的变化量与径向速度增量的关系为

升交点赤经和轨道倾角的变化量与法向速度增量的关系为

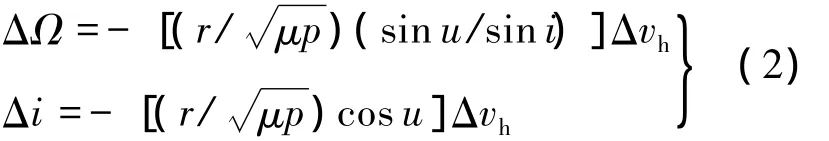
式中，a为轨道半长轴;p为半通径;e为偏心率;i为轨道倾角;Ω为升交点赤经;w为近地点幅角;θ为真近点角;r为地心距;u为纬度幅角;μ为地球引力常数.

2 远程自主制导策略

2.1 过程描述

初始时刻追踪航天器的轨道半长轴、偏心率、近地点幅角、升交点赤经、轨道倾角、真近点角分别为 ac0，ec0，wc0，Ωc0，ic0和 θc0，目标航天器的轨道要素分别为 at，et，wt，Ωt，it和 θt.本文假设 ac0＜at，即追踪航天器的高度低于目标航天器.要求在时间T内完成远程调相接近，使追踪航天器到达目标航天器后方且迹向距离为Δsf.可以根据两航天器的纬度幅角偏差与半长轴偏差的关系(文中提到的轨道要素偏差均为目标航天器减去追踪航天器的相应值)，将远程接近过程分为初始轨道飞行、调相轨道飞行和调整轨道飞行3个阶段，如图1所示.

图1 航天器的纬度幅角偏差与半长轴偏差的关系

初始轨道飞行阶段进行轨道共面修正和调相机动，其中共面修正由一次轨道法向脉冲机动实现.调相机动首先进行一次近地点幅角偏差修正，然后利用一次近地点和远地点的双脉冲变轨将追踪航天器从初始轨道调整到调相轨道，拉大两航天器的半长轴偏差.注意，如果初始半长轴偏差能够实现追踪航天器在任务要求时间内追上目标航天器，那么可以不进行这次改变半长轴偏差的调相机动.在初始轨道飞行期间，两航天器的纬度幅角偏差从Δu0降为Δu1，半长轴偏差由Δac0拉大至Δac1进入自然调相轨道.考虑追踪航天器初始状态与启控特殊点的最大偏差为1个轨道周期，这个过程最长需要1.5个轨道周期.

调相轨道飞行阶段由自然调相轨道过程和过渡轨道过程组成.在自然调相轨道上，追踪航天器不进行轨控，由于两航天器的半长轴偏差，纬度幅角偏差自然调整.当两航天器的纬度幅角偏差小于某个值Δumax1n(根据两个航天器的半长轴在轨解算)后，第1次经过近地点时两航天器的纬度幅角偏差的在轨测量值为Δu'1n，进行一次双脉冲变轨，减小半长轴偏差，追踪航天器从自然调相轨道进入到过渡轨道;然后再进行一次双脉冲变轨，两航天器的半长轴偏差降为预置值Δac20，追踪航天器从过渡轨道进入到调整轨道.设置过渡轨道的目的是为了保证进入调整轨道时两航天器的纬度幅角偏差为预置值Δus0.

调整轨道飞行阶段首先调整追踪航天器的远地点高度，使两航天器的远地点高度相同;然后根据两航天器的迹向距离要求，经过3次远地点脉冲变轨调整两航天器的半长轴偏差，最终使两航天器的近地点高度相同.由于在调相轨道飞行阶段存在较大的半长轴偏差，J2项轨道摄动会使两航天器的升交点赤经偏差变大，因此在调整轨道阶段还需一次共面修正和近地点幅角修正.在调整轨道飞行期间，两航天器的纬度幅角偏差从Δus0修正为最终期望值Δuf，半长轴偏差由Δac20修正为0.这个过程需要3个轨道周期.

根据以上过程描述，只有调整轨道的初始半长轴为预置参数，其余轨道的半长轴均需要在轨自主解算，以下3节将会分别给出各个飞行阶段半长轴的解算方法.另外，追踪航天器在各飞行阶段的偏心率均为预置参数.

2.2 初始轨道飞行期间变轨操作

初始轨道飞行进行轨道共面修正和调相机动.共面修正主要消除升交点赤经偏差和轨道倾角偏差，调相轨道的半长轴根据两航天器的纬度幅角偏差计算.追踪航天器在初始轨道运行一圈，追踪航天器超前目标航天器的纬度幅角为

其中，wt是目标航天器的平均角速度;Tc0是追踪航天器的轨道周期.

首先判断是否进行调相机动，若不进行调相机动，远程接近由初始轨道飞行和调整轨道飞行组成，调整轨道飞行期间半长轴偏差相对较小，纬度幅角偏差的变化量相对于初始轨道飞行可以忽略.调整轨道飞行需要3个轨道周期，当满足以下条件时，可以在规定的任务时间内完成远程接近，不需要进行调相机动.

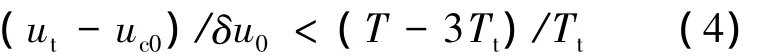
式中，uc0，ut分别是追踪航天器、目标航天器的初始纬度幅角;T是远程接近的总时间;Tt是目标航天器的轨道周期.

否则，调相时间将过长，需要进行调相机动.根据2.1节中的描述，追踪航天器在初始轨道运行1.5圈;在调相轨道向调整轨道过渡期间运行1.5圈;在调整轨道过程中运行3圈.则自然调相轨道的时间为

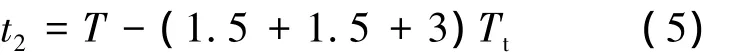
为了在规定时间内完成远程接近，则追踪航天器在自然调相轨道运行一圈，追踪航天器超前目标航天器的纬度幅角的期望值为

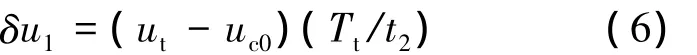
因此，追踪航天器自然调相轨道的轨道周期为

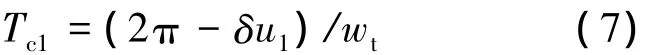
从而可以计算出自然调相轨道的半长轴ac1.

2.3 调相轨道飞行期间变轨操作

调相轨道到调整轨道的变轨过程如图2所示，从自然调相轨道到调整轨道共需要4次速度增量(Δv1－Δv4).期间经历3个半轨道周期弧段:各个弧段的时间分别为th1，th2和th3，其中th1由自然调相轨道的近地点高度和过渡轨道的远地点高度确定，th2为过渡轨道的半周期，th3由过渡轨道的近地点高度和调整轨道的远地点高度确定.

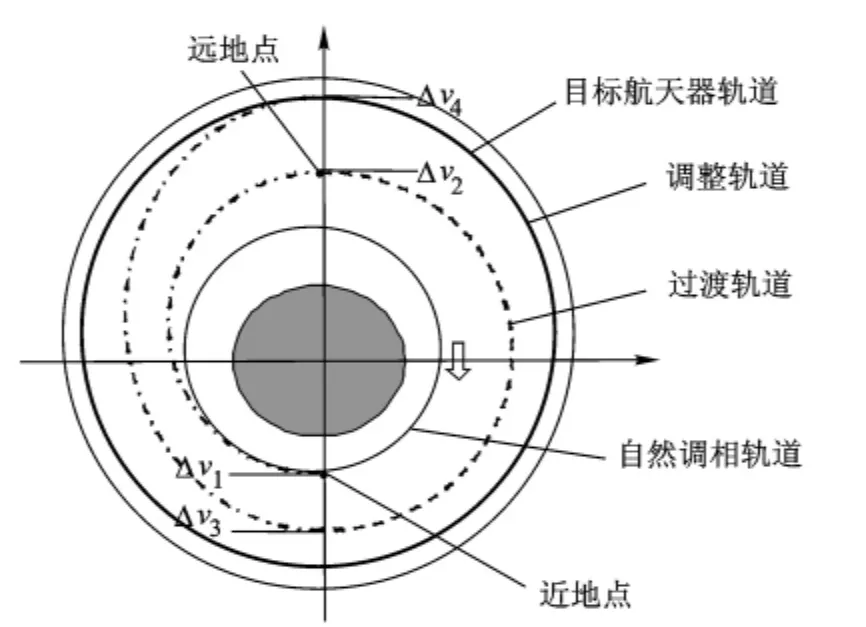
图2 调相轨道到调整轨道的变轨过程

过渡轨道的半长轴根据纬度幅角偏差解算.当追踪航天器进入调整轨道时，两航天器的纬度幅角偏差的期望值为Δus0.则在启动进入过渡轨道模式的初始解算点，两航天器的纬度幅角偏差Δu1n减去Δus0应正好等于追踪航天器赶超目标航天器的纬度幅角Δug，即

当过渡轨道与自然调相轨道重合时，过渡轨道启控点的纬度幅角偏差为最大值:

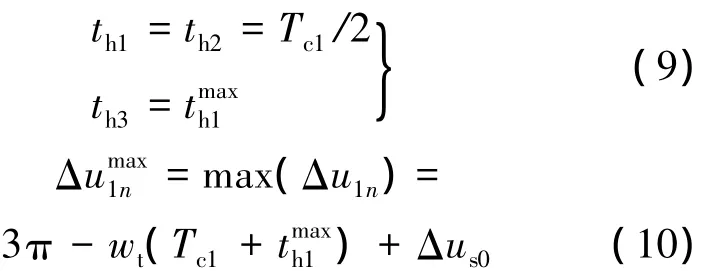
当过渡轨道与调整轨道重合时，过渡轨道过程启动点的纬度幅角偏差为最小值:

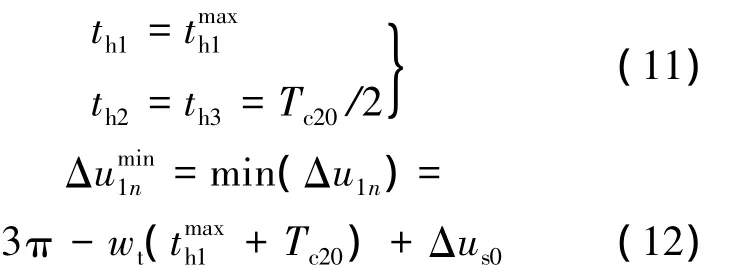
式中，Tc20为调整轨道的轨道周期;为由调相轨道的近地点到调整轨道的远地点经历的时间.

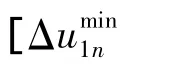
追踪航天器从自然调相轨道的近地点到调整轨道的远地点，追踪航天器超前目标航天器的纬度幅角的实际值为

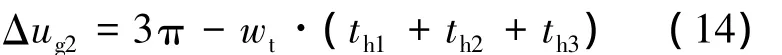
求解过渡轨道的半长轴利用搜索算法，从调相轨道的高度开始搜索，逐渐增大追踪航天器的半长轴，直到满足 Δug1＞Δug2.

2.4 调整轨道飞行期间变轨操作

追踪航天器进入调整轨道的远地点后，接下来的半圈轨道用于消除近地点幅角偏差、升交点赤经偏差和轨道倾角偏差.然后对轨道进行调整，首先在近地点变轨将追踪航天器的远地点与目标航天器的远地点高度相同.半长轴变化量由下式确定:

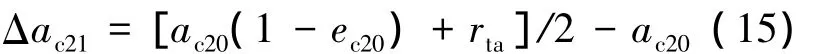
式中，rta为目标航天器的远地点与地心的距离.

如果任务要求追踪航天器从后方s2到sf处经一个轨道周期完成，则将远地点固定后，然后根据两航天器的迹向距离要求，分别经过3次远地点脉冲变轨调整半长轴偏差，最终使两航天器的近地点高度相同.

追踪航天器再次经过远地点时，假设两航天器的纬度幅角偏差为Δus1.期望下一次经过远地点时纬度幅角偏差为Δus2，则在一个轨道周期内，追踪航天器赶超目标航天器的纬度幅角的期望值为Δus1－Δus2，因此可以解算出第1次远地点变轨后追踪航天器的轨道周期:

同理，可以解算出第2次远地点变轨以后追踪航天器的轨道周期:

式中，Δuf为迹向距离Δsf对应的纬度幅角偏差.

第3次远地点变轨则期望将追踪航天器的轨道周期修正为与目标航天器的轨道周期相同，因此第3次变轨以后追踪航天器的轨道周期:

相应地，可以解算出追踪航天器各次远地点变轨的期望半长轴.

3 数值仿真

假设远程制导的主要约束指标包括:①要求追踪航天器在25 h内完成与目标航天器任意纬度幅角偏差的接近;②追踪航天器在目标航天器后方40～10 km的接近在一个轨道周期内完成;③远程制导结束，追踪航天器在目标航天器后方10±2 km的范围内保持一个轨道周期以上.

两航天器的初始平均轨道要素如表1所示，其中Re为地球平均半径.纬度幅角相差180°，式(4)不满足，需要进行调相机动.文中提到追踪航天器的预置参数如表2所示，追踪航天器推力使用脉冲控制.航天器轨道仿真模型采用Cowell法构建，轨道摄动加入地球扁率J234项，仿真步长为 0.4 s.

表2 追踪航天器的预置参数

图3给出了追踪航天器的速度增量，可见轨道横向进行10次变轨，横向速度增量为204.4m/s;轨道法向进行2次变轨，法向速度增量为102.5 m/s;轨道径向进行2次变轨，径向速度增量为4.8 m/s，整个远程导引过程所需要的速度增量为311.7 m/s.最后一次速度增量的施加时刻为23.86 h，满足时间约束要求.图4和图5给出了以目标航天器为中心的追踪航天器的相对运动轨迹:制导结束之后一个轨道周期内追踪航天器保持在目标航天器后方10±2 km范围内;轨道法向的精度为100 m.

图3 追踪航天器的速度增量

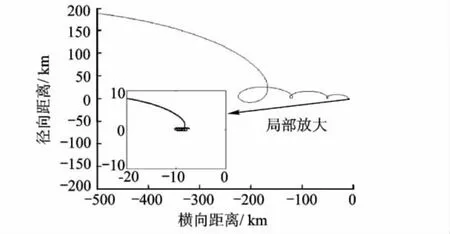
图4 轨道平面内的相对运动规律

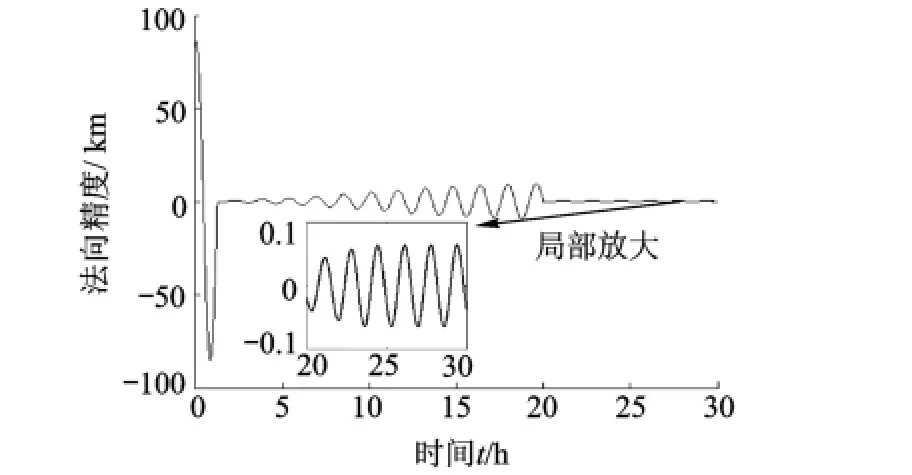
图5 轨道法向的相对运动规律

以上仿真结果满足远程制导的约束指标，表明本文设计的自主制导算法能够完成自主交会任务的远程调相接近段快速接近.

4 结论

本文研究了基于经典轨道要素的航天器自主交会远程快速接近算法.将远程调相接近段分为初始轨道飞行、调相轨道飞行和调整轨道飞行3个阶段，通过建立各个阶段纬度幅角偏差与半长轴偏差之间的关系，给出了特殊点变轨的脉冲制导方法.最后用精确的轨道模型对以上提出的自主制导算法进行了数值仿真.数值仿真显示本文提出的算法能够在满足远程制导约束的情况下实现快速精确接近.虽然文中假设追踪航天器轨道低于目标航天器轨道，但文中的算法仍然具有普遍性，对于追踪航天器轨道高于目标航天器轨道的情况，可以根据文中的分析对算法进行相应的改变即可.本文提出的算法计算量小，便于在轨自主实时运算，适用于交会对接任务的远程调相接近段自主快速接近.

References)

［1］Fehse W.Automated rendezvous and docking of spacecraft［M］.New York:Cambridge Univ ersity Press，2003:8－28

［2］朱仁璋.航天器交会对接技术［M］.北京:国防工业出版社，2007

Zhu Renzhang.Rendezvous and docking techniques of spacecraft［M］.Beijing:National Defense University Press，2007(in Chinese)

［3］Vander V A，Forbrich D.Use of aerodynamic shape optimization for a large transonic aircraft［R］.AA 97-2274，1997

［4］Prussing J E.A class of optimal two-impulse rendezvous using multiple-revolution lambert solutions［J］.Advances in the Astronautical Sciences，2000(106):17－39

［5］陈统，徐世杰.基于遗传算法的最优 Lambert双脉冲转移［J］.北京航空航天大学学报，2007，33(3):273－277

Chen Tong，Xu Shijie.Optimal Lambert two-impulse transfer using genetic algorithm ［J］.Journal of Beijing University of Aeronautics and Astronautics，2007，33(3):273－277(in Chinese)

［6］彭坤，徐世杰，陈统.基于引导性人工免疫算法的最优Lambert变轨［J］.北京航空航天大学学报，2010，36(1):6－9

Peng Kun，Xu Shijie，Chen Tong.Optimal Lambert transfer based on guiding artificial immune algorithm［J］.Journal of Beijing U-niversity of Aeronautics and Astronautics，2010，36(1):6－9(in Chinese)

［7］Carter T E.Fuel-optimal maneuvers of a spacecraft relative to a point in circular orbit［J］.Journal of Guidance Control and Dynamics，1984，7(6):710－716

［8］Dufour F，Garcia J M，Bemussou J，et al.Hermes-space station phasing strategies optimization［R］.IAF-91-345，1991

［9］吴会英，陈宏宇，余勇，等.远距离轨道接近及绕飞控制技术研究［J］.中国空间科学技术，2010，1(2):25－33

Wu Huiying，Chen Honyu，Yu Yong，et al.Study of long distance approaching and companion flying technology［J］.Chinese Space Science and Technology，2010，1(2):25－33(in Chinese)

［10］肖业伦.航天器飞行动力学原理［M］.北京:宇航出版社，1995

Xiao Yelun.Concept of space craft flight dynamics［M］.Beijing:Aerospace Publishing House，1995(in Chinese)