Optimization of the carrier tracking loop for GPS high dynamic receivers

LI Chuan－jun（李传军）， YANG Shu－xing（杨树兴）

（School of Aerospace Engineering，Beijing Institute of Technology，Beijing 100081，China）

It is needed to lower the noise bandwidth of the tracking loop and reduce the thermal noise and other interference to improve the tracking accuracy of the global position system （GPS）receiver.However，to lower the noise bandwidth of the loop may result in the signal lost abnormally in high dynamic case.Clearly，there is a conflict between the tracking capability and the tracking accuracy for the high dynamic receiver.Therefore，the optimization of the tracking loop and self adjusting the parameters of loop are the key factors of the design in order to adapt different dynamic behaviors and the variable signal powers，which affect the performance of the overall unit of the receiver.

Ref.［1］focuses on analyzing the optimal bandwidth design of the tracking loop in dynamic environment.Refs.［2－4］utilize the fuzzy con－trol theory to adjust the loop noise bandwidth and optimize the design，which heavily relies on personal experience or computer simulation，and may affect the tracking performance directly.Refs.［5－6］design the adaptive tracking loop mainly based on Kalman filter techniques and the wavelet denoising techniques，which deserve a large computation.For each channel of the receiver needs independent filter to deal with the tracked satellite，and the loop updating rate is much higher，the design will result in a huge amount of operation.Refs.［5，7］focus on the estimation of the LOS dynamic parameters which is crucial for the adjustment of the loop bandwidth adaptively.The measurement errors from the discriminator output are utilized to reduce the noise by means of a low－pass filter to estimate the dynamic stress.It will lead to some mistakes when the noise is large in our practical experiment.A high dynamic adaptive carrier tracking loop is advanced based on theα－β－γfilter，and the optimization methods for both tracking bandwidth and the carrier loop structure are analyzed in the paper.

1 Proposed tracking loop

1.1 Proposed carrier tracking loop

It is pointed out that most of the code tracking loop error can be reduced when aided by a carrier tracking loop［8］.The paper focuses on the design of carrier tracking loop，and a high adaptive carrier tracking loop structure is proposed，as shown in Fig.1.

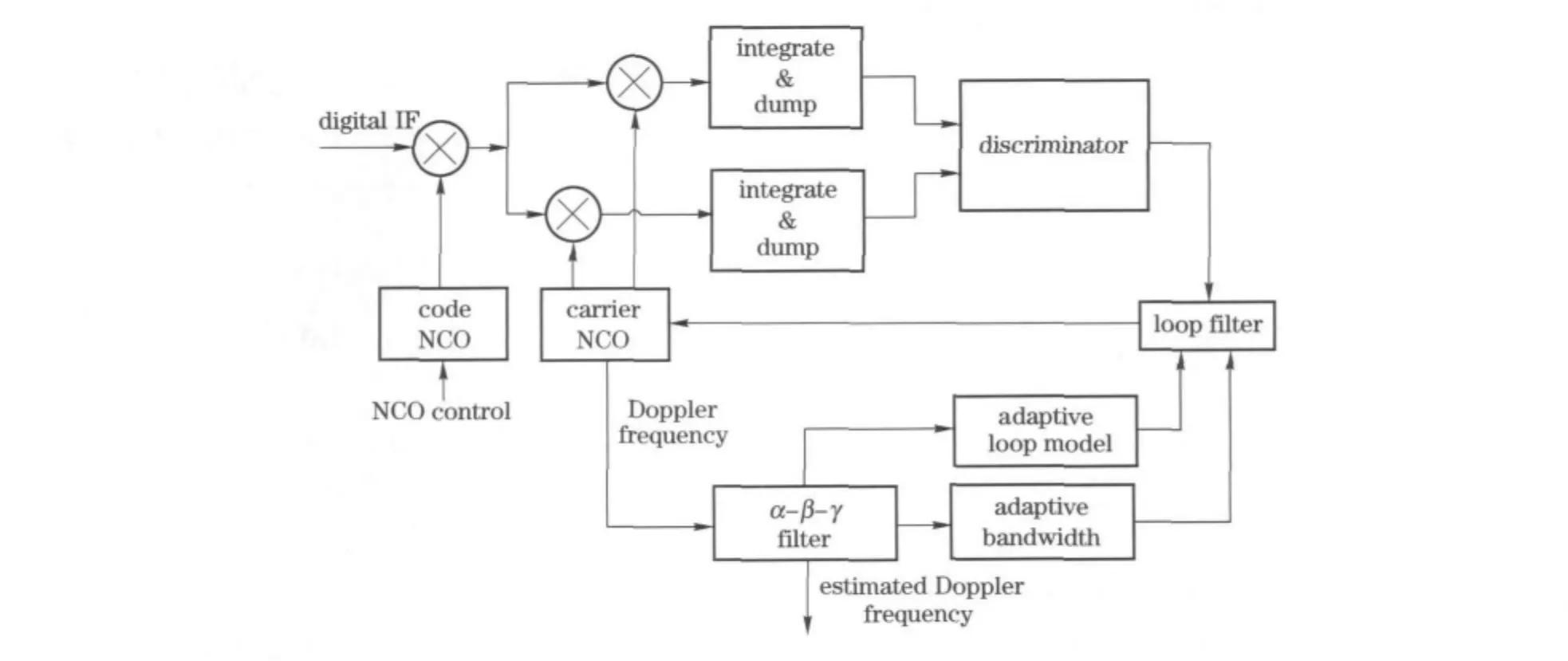
Fig.1 Proposed carrier tracking loop

Three modules，called theα－β－γfilter model，adaptive loop structure model and adaptive bandwidth model respectively，are added in the proposed carrier tracking loop compared with the traditional carrier tracking loop.The Doppler frequency gained from the carrier number controlled oscillator（NCO）is transferred to theα－β－γfilter to reduce the noise，and the estimated Doppler frequency as well as the dynamic parameters can be obtained.The estimated Doppler frequency is utilized by the navigation filter to calculate the speed of the receiver which will improve the accuracy of speed measurement.The estimated dynamic parameters are feedback to the adaptive loop model module to adjust the FLL assisting PLL filter’s structure and the PLL filter’s order，and the estimated dynamic parameters are feedback to the adaptive noise bandwidth module to calculate the optimized noise bandwidth of the PLL filter at the same time.In this way，the proposed carrier tracking loop structure can reduce the loop noise，improve the speed measurement accuracy，and satisfy the dynamic tracking capability.

1.2 System model

GPS IF signal can be modeled as［2］

whereAis the signal amplitude，D（iTs）is the navigation data bit，C（iTs）is the coarse PRN code，fIFis the intermediate frequency，φ（iTs）is the unknown carrier phase to be estimated，andN（iTs）is Gaussian white noise with zero mean and variance ofσ2.

The outputs of the integration and dump filter are

whereTis the pre－detection integration time，N＝Tfsis the number of samples，R（τ）is the autocorrelation function of C／A codes，Δφ＝π＾fdT＋＾θis phase misalignment，＾fdis frequency misalignment between incoming signal and local carrier replica.

The phase errorΔφand frequency errorΔ ω，which are the outputs of discriminator，are given by［2］

Fig.2 FLL assisting PLL filter design

The function of the loop filter is to reduce the noise and produce an accurate local carrier replica.The loop filter’s response to dynamic signal is determined by the loop order and the noise bandwidth.The first－order，second－order and third－order loop filter are sensitive to the velocity stress，acceleration stress and jerk stress respectively［8］.And a second－order FLL assisting a third－order PLL filter is used for a GPS high dynamic receiver［9］，which is shown in Fig.2.

The characteristic of the loop filter can be written as［8］

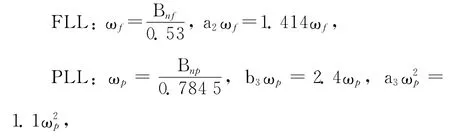
whereBnfis the second－order FLL loop filter noise bandwidth，and the third－order PLL loop filter noise bandwidthBnpis determined by the adaptive bandwidth algorithm based on theα－β－γfilter and the estimated carrier－to－noiseC／N0.

2 Optimization analysis

2.1 PLL tracking error

When the incoming signal is locked and the tracking loop is closed，the PLL measurement errors come from two major components：the noise error caused by the thermal noise and the steady error caused by the dynamic stress along the lineof－sight（LOS）between the receiver antenna and the satellite.

The PLL jitter due to the thermal noise is［8］

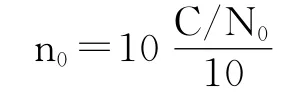
The PLL error for a third－order loop （PLL3）caused by the dynamic stress is［8］

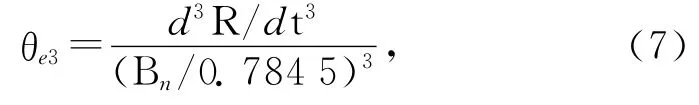
where d3R／dt3represents the maximum LOS jerk dynamics.

The rule－of－thumb tracking threshold for the PLL3is that the 3－σjitter must not exceed onefourth of the phase pull－in range of the two－quadrant arctangent discriminator.The 1－σ rule－ofthumb threshold for PLL tracking loop is therefore

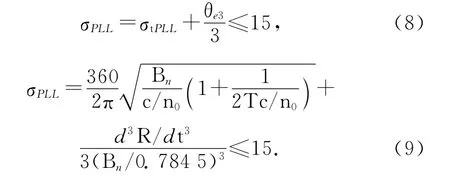
2.2 Optimization of loop bandwidth

From Eq.（9），it can be found out that the measurement errors caused by the thermal noise can be reduced by decreasing the noise bandwidthBnbut it will increase the errors caused by dynamic stress，when neglecting the effect of theC／N0.Actually，both the carrier－to－noise power rationC／N0and the dynamic stress d3R／dt3can be estimated in real time when the carrier loop is locked.And the optimization of the tracking loop bandwidth is just to choose the properBnto get the least PLL tracking measurement errorσPLL，and the proper bandwidth can be obtained by Eqs.（10）（11）［1］

then

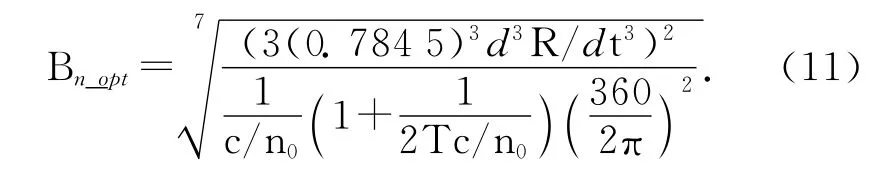
2.3 Optimizing carrier tracking Loop

Based on the analysis on the carrier loop order，the thermal noise and the dynamic stress errors above，an optimized scheme for the carrier tracking loop can be originated，which can be realized by：

Step 1Adopt a second－order FLL assisting third－order PLL to get the primary locked tracking loop.

Step 2Estimate theC／N0by power ration method［10］.

Step 3Estimate the relative velocity，accelarration stress and the jerks stress along LOS direction between the receiver antenna and the satellite using the carrier Doppler frequency calculated by the carrier NCO of tracking loop as the observation data ofα－β－γfilter in real－time.

Step 4Self adjust the loop order and loop structure according to the estimated accelarration and the jerks among LOS.

Step 5Calculate the optimized noise bandwidth from the LOS dynamic stress parameters and the carrier－to－noiseC／N0and update the carrier tracking loop noise bandwidth.

Step 6Return to step 2.

3 α－β－γ filter－based tracking algorithm

3.1 Dynamics model

The relationship among the dynamic stress parameters can be expressed as

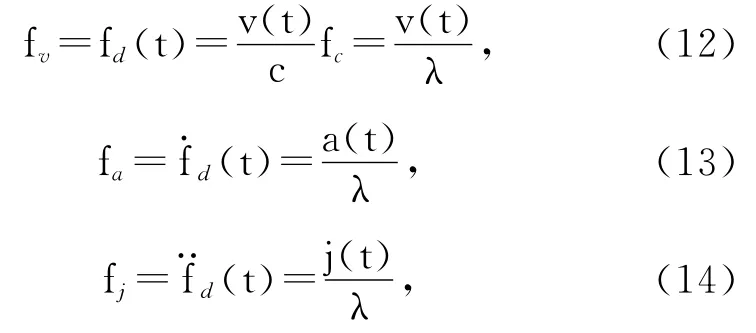
wherefvis the Doppler frequency of the incoming signal，fais the change rate of the frequency shift caused by the accelerationa（t）along the LOS，fjis caused by the jerkj（t），andλis the wavelength of the carrier signal.

From Eqs.（12）－（14），the dynamics model can be created.

And the measurement is modeled by Doppler frequency

whereTis the update period，both Wn（k）and Vn（k）are Gaussian white noise sequences.

3.2 α－β－γfilter

The optimal mean－square－error （MSE）estimation process for satellite tracking is given by prediction：

correction：

whereKis the steady－state Kalman gain and the optimal relationship amongα－β－γparameters is［11］

3.3 Improvingα－β－γfilter

Theα－β－γfilter is more popular for its much less computation due to the fixed coefficients resulted from the constant gain in the radar multi－objects tracking compared with the Kalman filter，but it may lose the high maneuver objects.A method is proposed to improve the filter’s dynamic response to meet high dynamic application by self adjustα－β－γfilter coefficient used in the tracking loop.

From Eqs.（20）（21），it can be found out that the function ofK，the coefficients of theα－β－γfilter，is to adjust the proportion of measurementZ（k）and the prediction value（k／k－1））to get the optimal estimated result（k）.The increase in the prediction residual（k／k－1）indicates the decrease in the prediction tracking effect and the increase in the gain is needed to enlarge the proportion ofZ（k）in（k），and vice versa.Thus the tracking performance can be improved by choosing the properαand theβ－γcoefficient can be obtained by Eqs.（21）（22）.

It is noticed that the measurement error is nearly proportional to the gain of the filter，and the stability of the tracking loop must be ensured when choosingα－β.And it is found that a simple function is suitable for the description of the relation between the measurement error and the filter gain by means of analysis and experiments，which can also improve the response of the filter［12］.The function is

wherebis a constant andxis an independent variable.The algorithm for the adaptiveα－β－γfilter is then described as

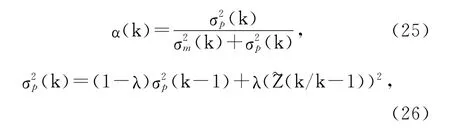
3.4 Estimation of dynamics

From Eqs.（15）－（26），an improvedα－β－γfilter can be achieved and the estimatedfv，fa，fjcan be obtained as well.The speed measurement precision will be improved by applyingfv，the filtered Doppler frequency，for the navigation solution.According to Eqs.（13）（14），a（t）andj（t）among LOS can be calculated to adaptively adjust the structure and bandwidth of the tracking loop.

4 Simulation results

A GSS7700GPS／SBAS Simulator from Spirent Communications is used to simulate the flight.The scenario is designed that the flight direction is east ward and the signals power is varied，as shown in Fig.3.The IF signals are collected by the GPS signal collection system.And the performance of three cases with different carrier tracking loops is analyzed and compared，in which：① 1－order FLL assisting 2－order PLL（FLL1PLL2）； ②2－order FLL assisting 3－order PLL （FLL2PLL3）；③adaptive carrier tracking loop based onα－β－γfilter（ACTLF）.The tracking satellite is SV3and the pre－detection integration time for the carrier tracking loop isT＝4ms for all cases.The bandwidth for FLL isBnf＝2Hz and PLL bandwidth isBnp＝16Hz in case①and②，while the optimal scheme presented above is utilized in case③.Simulation results are shown in Figs.4－8.

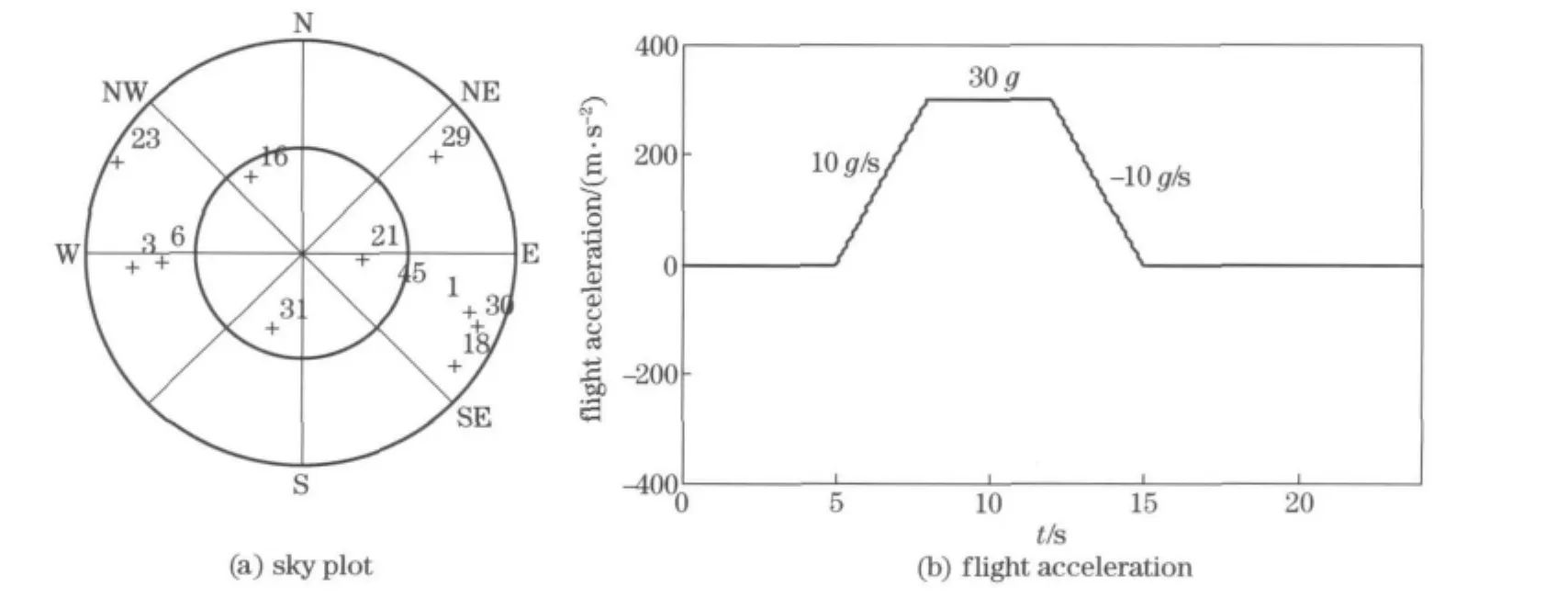
Fig.3 Flight scenario

Fig.4 Tracking error and estimated C／N0 in case 1（FLL1PLL2）

Fig.5 Tracking error and estimated C／N0 in case 2（FLL2PLL3）

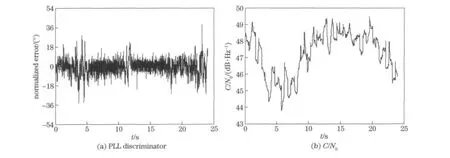
Fig.6 Tracking error and estimated C／N0 in case 3

Fig.4shows that FLL1PLL2can’t track the jerk signal in case 1.Fig.5and Fig.6show that FLL2PLL3and ACTLF can track the jerk signal in cases 2and 3.The output of the PLL discriminator indicates that the tracking error of ACTLF is less than FLL2PLL3.

Fig.7 Estimated dynamics parameters in case 3（ACTLF）

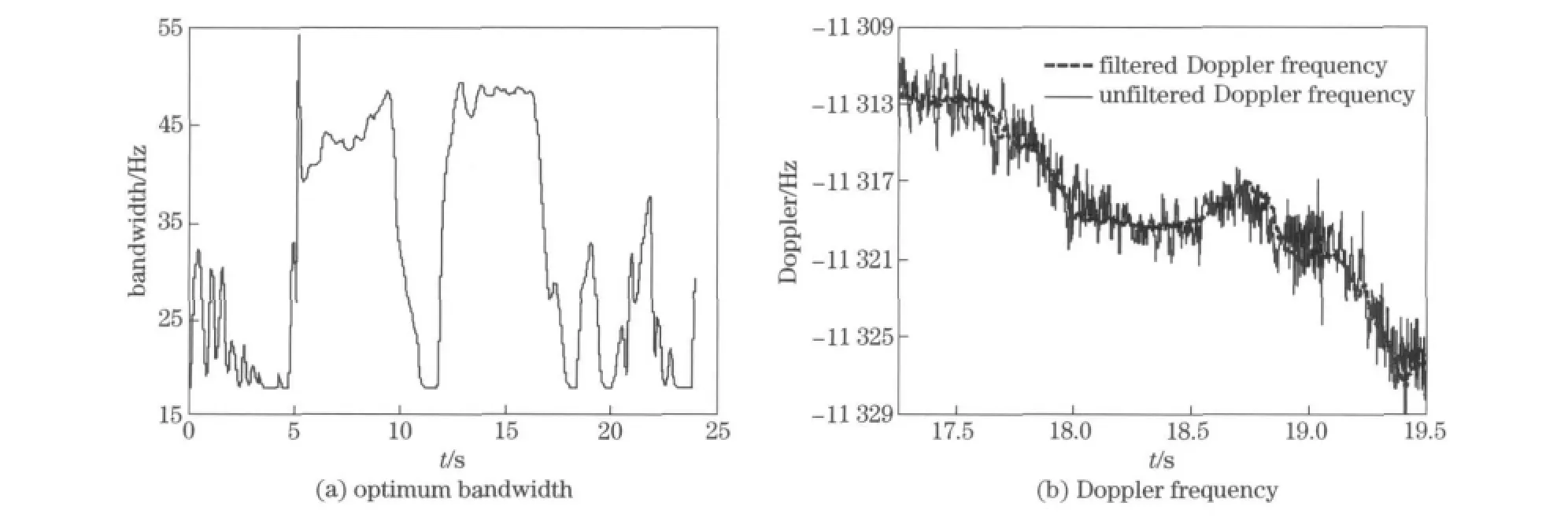
Fig.8 ACTLF bandwidth and filtered frequency in case 3

As the flight direction is the same，the acceleration and jerk along LOS between the SV3and the antenna are almost in proportion to the acceleration and jerk of the antenna respectively in flight.Fig.7and Fig.3indicate that the estimated dynamic parameters agree well with the actual situation.Fig.8shows that there is a greater change in the optimal loop bandwidth of ACTLF in the dynamic signal environment with variedC／N0，which verifies the optimization method works well.Fig.8indicates that noise of filtered Doppler frequency has been significantly reduced compared with the noise of unfiltered Doppler frequency，which makes clear that ACTLF improves the precision of the speed measurement.

5 Conclusion

A high dynamic adaptive tracking loop based on the novelα－β－γfilter is proposed in the paper in which theα－β－γfilter coefficients is self－adjusted based on the variance of prediction error and Doppler frequency measurement error to achieve the accurate estimate of high dynamic parameters along LOS，and the adaptive loop order and noise bandwidth of the filter is realized.Simulation results show that the algorithm can not only improve the high dynamic receiver's adaptive tracking ability，but also improve the accuracy of the loop measurement.

［1］Jwo D J.Optimization and sensitivity analysis of GPS receiver tracking loops in dynamic environments［J］.IEE Proc Radar，Sonar and Navigation，2001，148（4）：241－250.

［2］Mao W L，Tsao H W，Chang F R.Intelligent GPS receiver for robust carrier phase tracking in kinematic environments［J］.IEE Proc Radar，Sonar and Navigation，2004，151：171－180.

［3］Ahmed M Kamel.Design and testing of an intelligent GPS tracking loop for noise reduction and high dynamics applications［C］∥ION GNSS 2010，September，2010.Portland，Oregon：ION，2010.

［4］Tang B，Yu X Q，Dong X R.Design intelligent carrier tracking loop based on software GPS receiver ［J］.Journal of Beijing University of Aeronautics and Astronautics，2007，33（7）：807－810.（in Chinese）

［5］Lian P，Lachapelle G，Ma C.Improving tracking performance of PLL in high dynamics applications［C］∥National Technical Meeting of the U.S.Institute of Navigation.San Diego，California：ION，2005：1042－1052.

［6］Li J H，Ba X H，Sheraz A.Adaptive PLL based carrier tracking algorithm for GPS signals in high dynamic environments［J］.Chinese Journal of Electron Devices，2007，30（4）：1140－1443.（in Chinese）

［7］Zuo Q Y，Yuan H，Lin B J.Optimal algorithm research of GPS signal tracking loop under the high dynamic circumstance ［J］.Journal of Astronautics，2008，29（2）：550－555.（in Chinese）

［8］Kaplan E D，Understanding GPS：principles and appli－cations［M］.London，U.K.：Artech House，1996：153－240.

［9］Ward P.Performance comparison between FLL，PLL and a novel FLL－Assisted－PLL carrier tracking loop under RF interference conditions［C］∥Proc of the 11th ION／GPS.Nashville：ION，1998：783－795.

［10］Mohammad S Sharawi，Dennis M Akos，Daniel N Aloi.GPSC／N0estimation in the presence of interference and limited quantization levels ［J］.IEEE Transactions on Aerospace and Electronic Systems，2007，43（1）：227－238.

［11］Paul R Kalata.The tracking index：ageneralized parameter forα－βandα－β－γtarget trackers［J］.IEEE Transactions on Aerospace and Electronic Systems，1984，20（2）：174－182.

［12］Wang H L，Li F，Zhao Y G.An adaptive algorithm filter for maneuvering target tracking［J］.Radar Science and Technology，2007，5（4）：278－282.（in Chinese）

（Edited byWang Yuxia）