汽车制动颤鸣现象的数值分析方法研究*①

徐炜卿，吴光强，2，栾文博

(1.同济大学汽车学院，上海 201804;2.东京大学生产技术研究所，日本 东京 153－8505)

0 引言

随着中国汽车保有量的不断增长，城市交通状况日益恶化，拥堵的城市路况，常使汽车长时间处于走走停停的状态.大量的试验研究表明，制动颤鸣是一种发生在较低车速和较低制动压力下的低频制动振动噪声.驾驶员逐渐松开制动踏板时，汽车从静止状态开始运动，当制动压力逐渐降低，制动盘和摩擦块之间产生了滑移，此时制动压力依旧较高，制动盘的转速受到限制，从而导致了制动盘和摩擦块之间反复的粘合，由此造成了汽车的制动颤鸣现象［1－2］，其中，动摩擦系数和静摩擦系数之间的差值是制动盘和摩擦块之间的摩擦块之间的粘滑运动的产生的一个重要因素［3－4］.

目前对于机械系统的粘滑运动，通过计算机来仿真来准确模拟粘滑运动的两个表面之间的相对速度在零值附近时的强非线性特性仍非常困难［5］.本文基于上述求解过程中存在的问题，通过结合 M.Hénon求解庞加莱映射的计算方法与Runge－Kutta法，提出了一种求解分段的非线性系统的可行方法.

1 单自由度制动颤鸣模型

自激振动系统以自激的运动状态作为调节器，控制输入的能量，输入的能量与耗散的能量达到平衡，系统维持等幅运动.其中，汽车制动盘和摩擦块之间的粘滑运动，作为一个干摩擦自振系统，就是一种典型的自激振动［6］.图1为一个简单的干摩擦自振系统模型，这个经典的单自由度模型对于分析粘滑特性有着出色的效果［7］，被广泛应用用制动颤鸣现象的研究中.

图1 单自由度制动颤鸣模型

对该模型进行受力分析得到:

式中:m为摩擦块质量;k为摩擦块连接刚度;c为摩擦块连接阻尼;v0为制动盘恒定运动速度;Fn为摩擦块法向作用力;Ff为摩擦块制动力;μs为静态摩擦系数;μd为动态摩擦系数;Δμ为静态摩擦系数与动态摩擦系数之差.取状态变量，状态方程为

对于非线性系统，通过解析法来求解原系统的精确解往往非常困难，大部分只能取得近似的数值解，因此采用常用的Runge－Kutta法，设定一定的时间步长进行计算，在计算过程中发现，状态变量始终处于＞v0或是＜v0的情况下，而=v0的情况在运算时几乎不会触发，即实际的运算中，制动盘与摩擦块之间的运动始终处于滑移工况，而这与实际情况显然是不符的.

对某配备自动变速箱汽车进行制动颤鸣实验，由驾驶员逐渐松开制动踏板，汽车从静止开始启动，当颤鸣现象发生时，通过对制动钳处采集到的加速度信号进行分析后，发现其中存在着周期性的粘滑运动.

图2 粘滑运动相图

在非线性振动理论中，汽车制动颤鸣现象中的粘滑运动可以看作是自激振动系统中的一个稳定极限环，是一种与极限环相对应的周期运动［6，8］.通过图2 中运动的相轨迹可以发现，其运动的周期性不明显，且=v0的情况未触发.为了解决这一问题，比较简单的办法是将=v0的情况适度放大，即为摩擦块与制动盘之间的粘合运动增加一个阈值，认为当－C≤v0－≤C时即为粘合状态，将摩擦块所受摩擦力改写为

采用Runge－Kutta法进行数值计算，观察其相轨迹如图3所示，可以发现，周期性明显得到了改善.

图3 阈值C=0.01时的粘滑运动相图

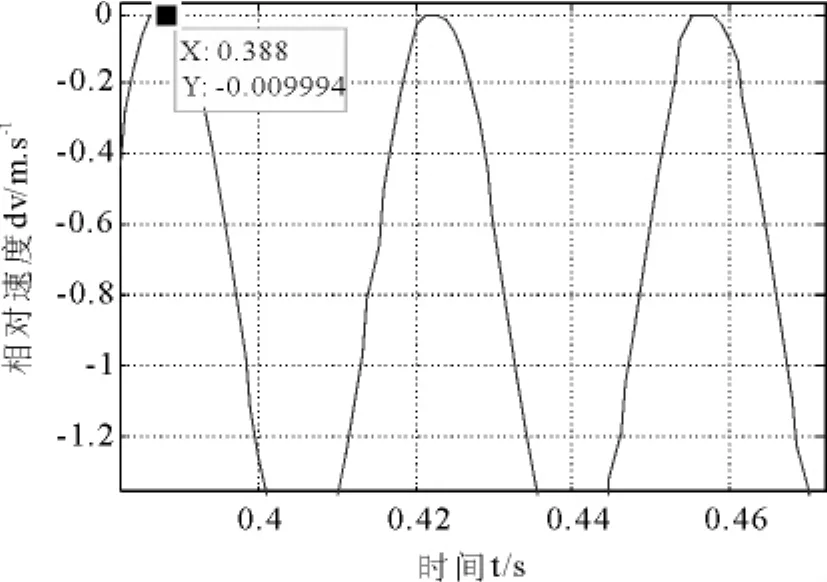
图4 阈值C=0.01时的制动盘和摩擦块之间的相对速度

图5 阈值C=0.01时的摩擦力图

图6 Runge－Kutta法与Hénon法结合分析所得相图

图7 Runge－Kutta法与Hénon法结合分析所得相对运动速度

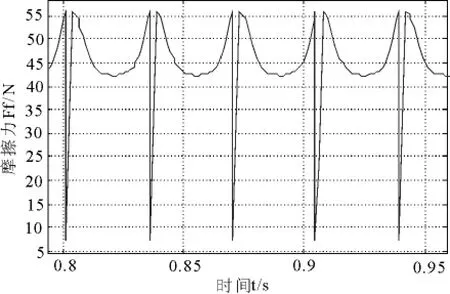
图8 Runge－Kutta法与Hénon法结合分析所得摩擦力图

尽管通过增加阈值，改善了粘滑运动的周期特性，但从图5中，可以发现，在粘滑运动的每个周期内，粘合和滑移的临界点(图5中实线圈和虚线圈)处的摩擦力存在偏差，而通过理论分析可以知道，该临界点(上极值点)处的摩擦力μsFn应为最大静摩擦力，且实线圈与虚线圈中的极值点大小应相同，而每个周期内的摩擦力下极值点也应当大小相同.即采用Runge－Kutta法直接进行求解时，对于摩擦块在任意两个运动周期内计算得到的结果，表示在相图中时，往往是处于不同位置处的相点，因此也不利于找出准确的周期.

2 Hénon法原理

M.Hénon在计算庞加莱映射时，即计算相轨迹与庞加莱截面之间的交点时，提出了一种对交点的计算方法［9］.

假设一个N维的动力学系统I的微分方程为

运用一个N－1维的超平面Σ(庞加莱截面)与该微分方程组在相空间内的运动轨迹的交点，从而获取庞加莱映射，此平面的方程如下

通常，庞加莱截面的平面方程并不是显式方程，为了获取庞加莱映射，往往增加一个新的变量

从而在微分方程中增加一个新的方程

当新系统II的相轨迹靠近该截面，当检测到xN+1的正负符号在零值附近变化时，即xN+1的值由大于零转变为小于零，或由小于零转变为大于零时，将其方程改写成系统III如下形式

这样，时间t转变为状态变量，假设在相轨迹中，xN+1的正负符号变化前的最后一个点所对应的xN+1=x*，以xN+1∈［x*，0］对各变量进行积分，得到各变量［x1，x2，…，xN，t］的值.

3 结合Hénon法与Runge－Kutta法的数值方法

现将M.Hénon计算庞加莱映射中所用的数值计算方法应用到汽车制动颤鸣现象的粘滑运动的数值计算中.首先对方程(3)、(4)所描述的单自由度粘滑运动模型通过Runge－Kutta法进行计算，当摩擦块的运动速度穿越粘合点，即x2－v0值的正负号发生变化时，以x2－v0值的正负号变化前一时刻的系统各状态变量的值(设为x*)作为初始值，对状态变量x2在［x*，0］范围内进行积分，时间t作为新的状态变量，将原状态方程转换为

之后再以龙格库塔法进行数值计算，重复这一过程从而完成整个运算过程.

通过在这两个系统之间的切换完成对单自由度颤鸣模型的数值计算，图6与图3中采用设定阈值的方法相比其周期性更为明显;将图7与图4相比，可以看到此方法不存在因阈值而存在的偏差;比较图8与图5，Runge－Kutta法与Hénon法结合所得到的摩擦力在每个周期内都保持了非常高的一致性.实际上，用Runge－Kutta法对每个周期内的运动进行数值计算，当两个摩擦面之间的运动速度在粘合点附近时，Hénon法重新计算了相对速度的极值点，相对于在每个运动周期内进行一次“校准”，从而有利于对其周期运动的进一步分析

4 结论

在分析汽车制动颤鸣现象时，运用Runge－Kutta法与Hénon法结合的方法计算其粘滑特性取得了令人满意的结果，并得出了以下结论:

(1)本文提出的方法对于汽车制动颤鸣现象在分析精度上高于设置阈值所取得的结果，并且无需考虑阈值大小的选取问题.

(2)在汽车上存在着大量的分段的非线性元素，不仅制动器，离合器接合过程中也存在着粘滑特性，在计算分析时都会遇到分段函数的边界值问题，对于这些汽车上大量存在的分段的非线性问题，本文所提出方法不失为一种可行的数值计算方法.

［1］Zahrul Fuadi，Koshi Adachi，Hideaki Ikeda，et al.Effect of Contact Stiffness on Creep－groan Occurrence on a Simple Caliper－ slider Experimental Model［J］.Tribol Lett，2009(33):169－178.

［2］Mark Donley，Dave Riesland.Brake Groan Simulation for a McPherson Strut Type Suspension［C］.SAE paper 2003－01－1627.

［3］布尚(美).摩擦学导论［M］.北京:机械工业出版社，2007:132－134.

［4］M.Bettella，M.F.Harrison，R.S.Sharp.Investigatiion of Automotive Creep Groan Noise with a Distributed－source Excitation Technique［J］.Journal of Sound and Vibration，2002，255(3):531－547.

［5］Jan Awrejcewicz，Pawel Olejnik.Occurrence of Stick－slip Phenomenon［J］.Journal of Theoretical and Applied Mechanics，2007，45(1):33－40.

［6］刘延柱，陈立群.非线性振动［M］.北京:高等教育出版社，2001:126－132.

［7］H.Hetzler，D.Schwarzer，W.Seemann.Analytical Investigation of Steady－state Stability and Hopf－bifurcations Occurring in Sliding Friction Oscillators with Application to Low－frequency Disc Brake Noise［J］.Communications in Nonlinear Science and Numerical Simulation，2007(12):83–99.

［8］Marcus Neubauer，Cord－Christian Neuber，Karl Popp.Control of Stick－slip Vibrations［C］.ITUAM Symposium on Vibration Control of Nonlinear Mechanisms and Structures，2005:223 －232.

［9］M.Hénon.On the Numerical Computation of Poincaré maps［J］.Physica 5D，1982:412－414.