方形土楼屋盖风荷载的数值模拟分析＊

彭兴黔 吴仁伟 徐 刚

（华侨大学土木工程学院 泉州 362021）

沿海地区台风活动频繁，台风经常造成大量建筑物，尤其是量大面广的低矮房屋的损坏甚至倒塌［1］.分布在沿海地区的客家土楼也遭到了台风的侵袭.“福建土楼”具有极高的历史价值、艺术价值和科学价值.2008年7 月7 日，“福建土楼”获准列入《世界文化遗产名录》，现代建筑师们从土楼身上获得灵感，一座座融合了传统间土楼建筑元素的现代建筑拔地而起［2］，借鉴并传承着土楼的血液与命脉，续写着古今交融、中外合璧的建筑风采.本文的客家土楼特指闽西永定土楼，在永定县内方形土楼现存4000多座［3］，形式多种多样.文中采用数值模拟方法［4－5］对土楼的风荷载特性和风流场进行分析，提出了适合于客家土楼的抗风措施，用以保护土楼，所以是十分有意义的.

1 数值风洞模拟

1.1 数值风洞与计算模型的选择

德辉楼［6］为原型建立了数值风洞模型（见图1），原型平面尺寸为面宽38m，进深32m ，檐口高度为11.2 m，挑檐挑出长度2.0 m，屋面坡角25°，土木内通廊式结构.数值风洞采用CFX－10.0中SSTk－ω 湍流物理模型，它对分离流的效果比较好［7］；因方形屋盖体型复杂，采用适应性强的四面体网格划分建筑模型［8－9］.

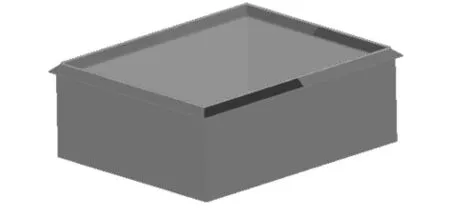
图1 德辉楼模型

1.2 数据处理方法

客家土楼墙体较厚，一般在1～2 m，受风影响小；而屋盖挑檐悬挑过长，台风首先破坏的是土楼的挑檐部分.如图2双坡屋盖分为内、外挑檐，外檐分区以Wi（i＝1～8）表示，内檐分区以Ni（i＝1～8）表示，对屋面风荷载进行数值模拟计算.为了便于比较分析不同坡角和高宽比对屋盖风荷载的影响，本文采用数值模拟方法，对在屋盖坡角为25°，高宽比分别为0.15，0.25，0.35，0.45，0.55和高宽比为0.35，屋盖坡角分别为15°，25°，35°，45°，60°的一系列模型，并分别对其在0°，45°，90°3个风向角下的风荷载分布特性进行了数值模拟.探讨了屋盖各区块的风压系数在不同坡度和高宽比的变化规律，分析结果可为沿海地区类土楼形式的现代建筑抗风设计提供参考.

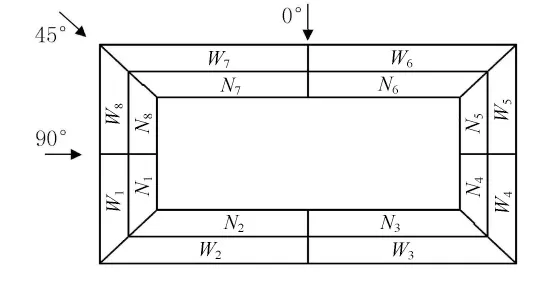
图2 屋盖表面分区

1.3 基本方程及湍流模型的选择

1.3.1 控制方程选择 采用由湍流模型封闭控制方程进行求解的时均模拟方法，气流流动控制方程［10］的通用形式，即

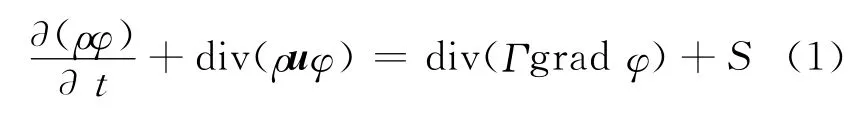
式中：各项依次为瞬态项、对流项、扩散项和源项.ρ为空气的质量密度；u 为速度矢量；φ 为通用变量；Γ 为广义扩散系数；S 为广义源项.

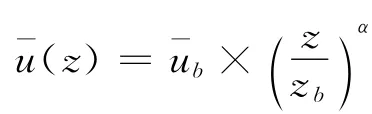
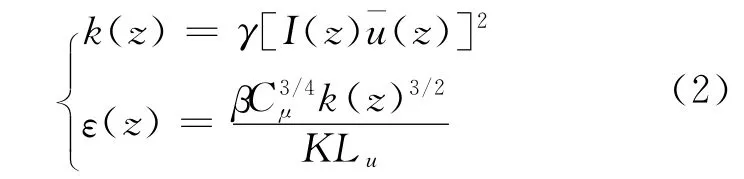
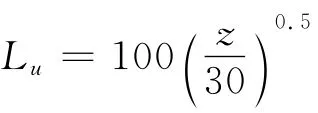
2 坡角和高径比影响的数值分析

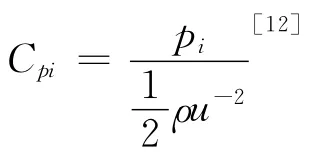
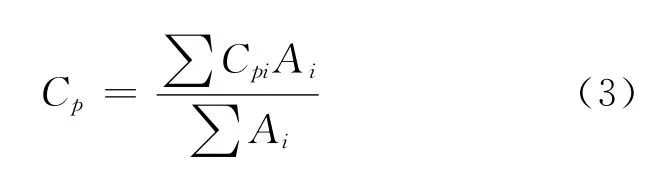
式中：Cpi为建筑物表面某测点i 的风压系数；pi为测点i的净风压力；为参考高度的平均风速；ρ为空气质量密度.通过将屋面上下表面分区，用上、下表面平均风压的差值来表征屋盖的净风压系数ΔCp，如下式：

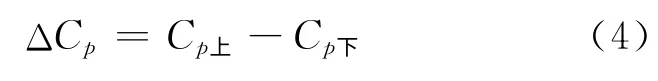
式中：Cpi为建筑物表面某测点i 的风压系数；pi为测点i的净风压力；为参考高度的平均风速；ρ为空气质量密度.

2.1 不同风向角下屋盖净风压系数随坡角变化曲线的数值分析

图3给出了屋盖内外挑檐区的净风压系数随坡角变化曲线，可以看出：（1）0°风向角时，只有外挑檐的W6区与W7区受坡角变化影响较大，坡角增大，W6区和W7区变化趋势一样，净风压系数减少幅度很大，由－1.84 变化到－0.77；内挑檐区净风压系数有正有负，随坡角变化幅度很小，在±0.2以内；（2）45°风向角时，随着坡角的增大，净风压系数减少很明显，特别是外挑檐区，W8区变化幅度最大，由－1.83 变化到－0.56，W1区由－1.21 变化到－0.55，W6区由－1.36变化到－0.60，W7区由－1.61变化到－0.63，充分说明屋盖坡角的增大有效较小净风压系数的负压值分布；（3）90°风向角时，内挑檐区的净风压系数基本无变化，外挑檐区只有W1区与W8区变化明显，随着坡角增大，净风压系数变化幅度较大，W1区由－1.56 变化到－0.63，W8区 由－1.79变化到－0.77.增大屋盖坡角在一定程度上能改善净风压系数的不利分布.

2.2 不同风向角下屋盖净风压系数随高宽比变化曲线的数值分析

图4给出了屋盖内外挑檐区的净风压系数随高宽比变化曲线，可以看出：（1）0°风向角时，对于外挑檐，净风压系数大都为负值，只有W1区和W8区的净风压系数受高宽比影响，高宽比增大，净风压系数绝对值增大，幅度比较小，W1区与W8区变化相似，绝对值由1.66变化为2.18；内挑檐区只有N4区与N5区随高宽比增大，净风压系数系数由负值转为正值；（2）45°风向角时，净风压系数绝大部分为负值，对于外挑檐区，W1区、W2区与W3区以0.45为临界高宽比，当高宽比为0.15～0.45时，净风压系数绝对值减小，当高宽比在0.45～0.55 时，净风压系数绝对值增加，W8区随着高宽比增大，净风压系数绝对值增大，变化幅度较小；内挑檐区净风压系数随着高宽比增大，绝对值减小，变化幅度较大；（3）90°风向角时，外挑檐区只有W2区与W3区受高宽比影响，变化幅度较小，由－1.42变化到－2.0；内挑檐区有N6区与N7区随高宽比增大，净风压系数增大.

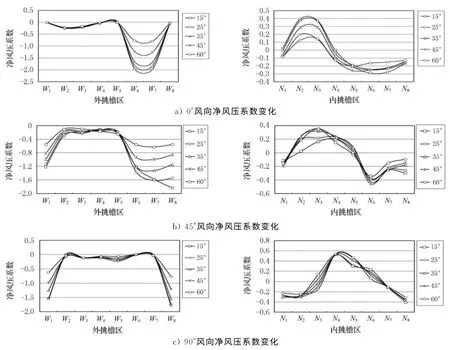
图3 不同风向角下屋盖净风压系数随坡角变化曲线

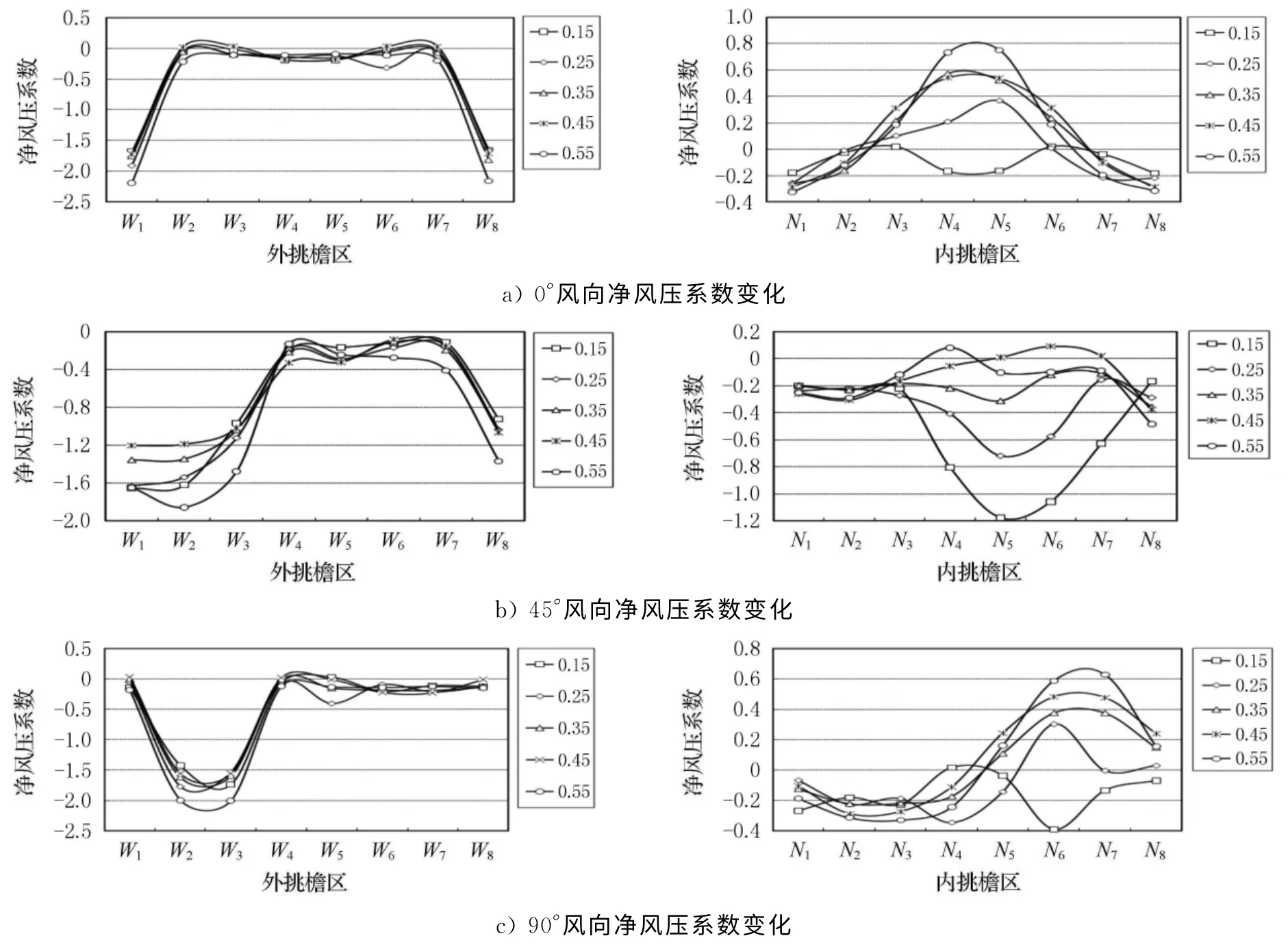
图4 不同风向角下屋盖净风压系数随高宽比变化曲线

2.3 高宽比对方形土楼风流场的影响

风速矢量图（见图5）可以看出，高宽比对方形土楼风流场的影响主要集中在土楼内部和屋盖挑檐处.高宽比为0.15时，方形土楼内部的湍流没有强烈扰动，没有出现环形涡流，屋盖的挑檐处分离比较均匀稳定；当高宽比逐渐变大时，檐口高度增大，宽度相对变小，土楼内部的环形涡流越来越明显，表现出了较强的湍流非各向同性.当土楼的高宽比达到0.55时，内部形成强度较大的环形涡流，来流在屋盖挑檐处产生很剧烈的分离，在檐口附近出现离散的小涡旋，使得檐口处产生了局部的高负压区，同时在背风面形成一个较大的涡流区，由于近背风表面处的风速明显减小，表明该处形成较小的负压.

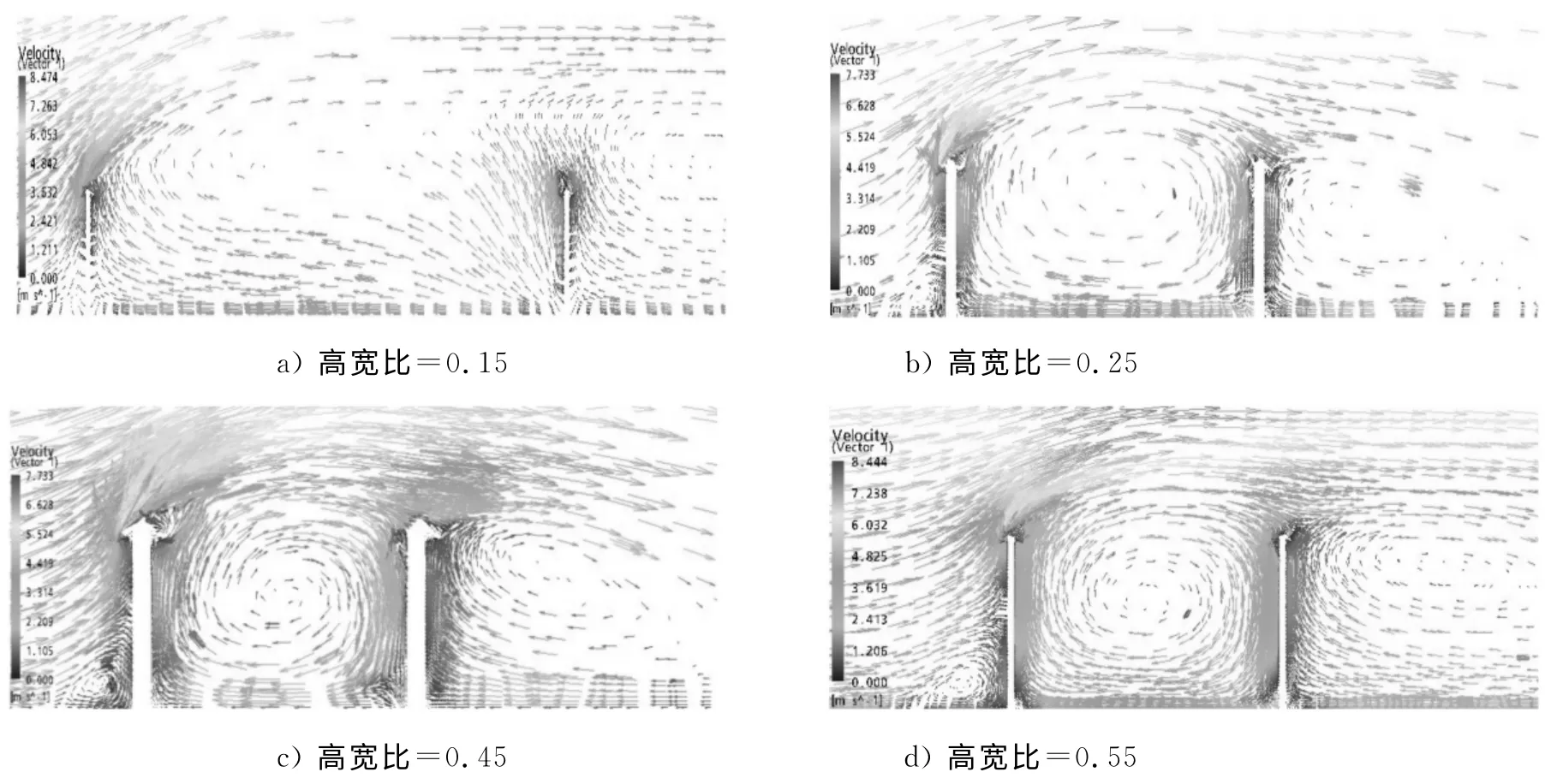
图5 不同高宽比下0°风向中心竖直剖面风速矢量图

3 结 论

1）在不同风向角下屋盖坡角对迎风的外挑檐区影响较明显，随着坡角的增大，其极值风压系数及净风压系数的负压绝对值均减小，甚至出现正压；屋盖下表面或内挑檐区受坡角影响较小，综合考虑三种风压系数对屋盖挑檐的影响以及流场分布的特点，屋盖坡角宜取45°左右.

2）土楼的高宽比变化影响了屋盖表面的风压分布，不同风向角下随着高宽比逐渐增大到0.45时，两种风压系数都相应的减小.同时屋盖挑檐附近流场分布均匀，土楼内部的环形回流改善居住的风环境，则高宽比为0.45左右对屋盖抗风有利.

［1］孙炳楠，傅国宏，陈 明，等.94年17号台风对温州民房破坏的调查［J］.浙江建筑，1995（4）：19－23.

［2］韩振华，赵 娟.走向未来的客家土楼［J］.福建建设科技，2009（1）：53－56.

［3］胡大新.永定客家土楼研究［M］.北京：中央文献出版社，2006.

［4］TAMURA T.Reliability on CFD estimation for wind－structure interaction problems［J］.Journal of Wind Engineering and Industrial Aerodynamics，1999，81：117－143.

［5］李 黎，尹 鹏，王开明，等.不同风向角动风下大跨越输电塔风振响应分析［J］.武汉理工大学学报，2009，31（23）：68－71.

［6］赵 杰.福建土楼：适中“典常楼”初探［D］.上海：同济大学，2006.

［7］陈景仁.湍流模型及有限分析法［M］.上海：上海交通大学出版社，1989.

［8］STATHOPOULOS T，BASKARAN A.Computer simulation of wind environmental conditions around buildings［J］.Engineering Structures，1996，18（11）：876－885.

［9］BASKARAN A，STATHOPOULOS T.Computational evaluation of wind effects on buildings［J］.Bldg Environ，1989，24（4）：325－333.

［10］王福军.计算流体力学分析－CFD 软件原理与应用［M］.北京：清华大学出版社，2004.

［11］RICHARDS P J，HOXEY R P，SHORT L J，Wind pressures on a 6mcube［J］.Journal of Wind Engineering and Industrial Aerodynamics，2001，89：14－15.

［12］张相庭.工程抗风设计计算手册［M］.北京：中国建筑工业出版社，1998.

［13］周暄毅.大跨度屋盖结构的风荷载及风致响应研究［D］.上海：同济大学，2004.