事故车辆局部变形精细计算与模拟系统＊

袁望方 魏 朗 陈 涛

（长安大学汽车学院 西安 710064）

确定汽车碰撞前速度是进行汽车碰撞固定物事故再现和事故原因分析的关键所在.常用的确定方法分为理论计算（运用动能定理、动量定理等）和借助工具进行经验判断.公安部《典型交通事故形态车辆行驶速度技术鉴定》（GA／T643－2006）中给出了车辆撞击固定物时的v－c关系式［1］.上海交通大学曾以10～80km／h的速度进行某车型有限元模型的虚拟正面碰撞试验进行事故发生前车速分析［2］.大连理工大学对多种轿车车身建模进行了130余次模拟碰撞分析计算建立汽车碰撞前速度和变形深度的关系模型［3］.这些研究成果的共同点是运用刚度系数进行车速分析，仅局限于少数碰撞形态与试验相类似的实际事故［4］.由于事故参与车型和碰撞方式多种多样，本文采用有限元理论将汽车碰撞变形区域进行简单网格划分，并采用车辆运动力学、动能定理、动量定理和弹性力学理论，结合多种汽车碰撞变形共同点，建立汽车碰撞前速度和变形区域关系的精细计算模型.

1 车辆变形结构及特征研究

通过大量事故案例统计得出主要事故车型统计相应车型的碰撞位置结构特征，其中包括各车型（轿车、客车、货车）的正面、侧面、后面位置结构特征以及部件材料构成.运用Handyscan EXAscan手动扫描仪进行主要碰撞位置及变形特征参数的提取，得到变形位置的最大变形深度、最大变形宽度.采用车辆动力学，弹性力学和有限元方法的理论，进行汽车碰撞固定物有限元计算模型建模.通过事故发生前后位置结构的特征估算变形吸收的能量，得出事故发生前一瞬间各汽车的动能，进而得出各车碰撞前车速.

2 事故车辆变形区域分析

2.1 车辆变形区域的有限元分析过程

有限元方法的基本思想是将连续的求解区域离散为一组有限个且按一定方式相互联结在一起的单元的组合体.由于单元能按不同的联结方式进行组合，且单元本身又可以有不同形状，因此可以模型化几何形状复杂的求解域.汽车碰撞变形是一个大型三维问题，可以采用逼近的方法来解决：（1）用假想的线或面将连续体剖分成若干个“有限单元”；（2）假想这些单元由位于边界或内部的许多离散点连接；（3）选择一系列基于节点位移的函数去唯一定义每个有限单元内部和边界上的位移状态；（4）根据节点位移的位移函数可以唯一确定出单元内部的应变状态，这些应变以及初始应变和材料的本构关系将一起定义出单元内以及边界上的应力状态；（5）确定出各种各样的力，包括集中在节点上的力、均衡边界应力和任意的分布载荷.

2.2 六面体网格生成算法

由于汽车车身表面通常为曲面，本研究对事故车辆变形部位变形前后划分网格，进行网格划分时采用10节点曲边四面体（如图1）转换为六面体网格.算法步骤如下［5］.

步骤1 首先，对分析域生成10节点曲边四面体网格（以下简称TET 10）.连接采用激光扫描仪对碰撞事故车辆变形部位扫描提取的特征点，生成多个曲边四面体网格.

步骤2 判断每个TET 10单元的单元边是直边还是曲边.这需要判断弦AB （如图2）中点M 的坐标和单元边中点E 的坐标是否相等，如相等，则单元边AB 为一直边；否则，为一曲边.

步骤3 计算每个TET 10单元的4个直边三角形的形心PABC，PABD，PBCD，PACD.

步骤4 对于TET 10 单元的每个单元面，判断是否存在曲边，如存在，该单元面为曲面，利用6节点曲边三角形单元的形函数，把该单元面的直边三角形的形心映射到曲面上.映射的方法如

其中：形状函数Ni（i＝1，…，6）定义为Ni＝Li（2Li－1），i ＝1，2，3；N4＝4L1L2；N5＝4L2L3；N6＝4L1L3.

步骤5 计算每个TET 10单元的内接直边四面体的形心，得到O 点.

步骤6 判断TET 10 单元是否存在曲边，如存在，利用10节点曲边四面体单元的形函数，把O 点映射到一个新的位置O.映射的方法类似于以上所述的曲面映射.采用映射的原因是：连接映射点和其他相关点得到的六面体单元面的翘曲最小.

步骤7 连接O 和其他相关点，把每个TET10分为4个六面体单元.

步骤8 排除重节点，并对单元和节点重新编号.

步骤9 判断节点的属性，即求出每个节点和被划分物体边界的最短距离，如该距离小于某一规定值，则该节点为边界节点，否则为内部节点.

图1 10节点曲边四面体单元

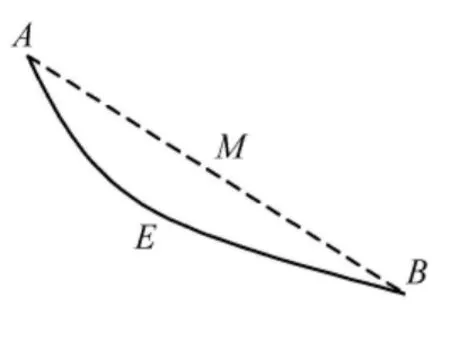
图2 判断单元边是否是曲边

3 碰撞瞬间力计算模型

根据有限元方法基础理论，处理连续体问题的有限元分析过程为：（1）将连续体划分为有限数目的块体（单元），这些块体的性质可用有限数目的变量来描述；（2）这些单元按照标准离散体系中所用的规则进行组装后，可以求得整体系统的解.

考虑一个标号为（1）的典型单元，它的节点编号为1，2，3，则可以根据节点位移、作用到单元上的分布载荷p 以及它的初始应变来惟一地确定出作用在节点上的力.假设单元的行为是线弹性的，则作用在节点上的力为

为了求得一个完整的解，必须满足以下2个条件：位移协调；受力平衡.则作用在节点i上的作用力为

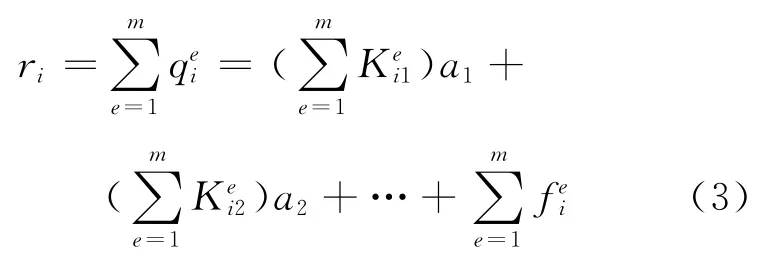
这个求和只针对与节点i相连的单元进行，将所有的这些方程组装起来，可得系统方程，Ka＝r－f.式中：

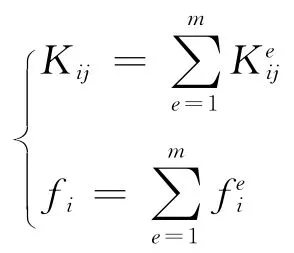
如果使用了不同类型的单元，并且将这些单元进行耦合，则在进行矩阵叠加时，必须要求它们具有相同的矩阵大小.本研究将依据该连续体问题的有限元分析过程，依托所提取获得的变形特征数据，进行事故车型的车身变形前碰撞力计算.

4 碰撞瞬间速度计算模型

若位移和相应载荷的乘积之和为真实的外部功，而应变和相应应力之和为全部的内部功.本研究采用基于有限元理论的碰撞变形能网格图对车辆碰撞前车速与车体变形件关系进行定量分析.汽车碰撞变形能网格图是指将车身划分为若干区域，求出各区域受撞击溃缩后所吸收的能量值.将事故车辆的完好状态下实际变形与网格图进行对比时，变形曲线与完好状态下的车型轮廓线之间区域所包含的数值总和即车身溃缩吸收的能量.首先，作以下假设：（1）汽车在全宽上任一点处垂直方向上的变形量相同；（2）碰撞过程中汽车与地面间的摩擦力忽略不计；（3）碰撞后汽车的弹性恢复忽略不计.由此得出变形能计算公式

式中：f 为单位车身宽度受到的碰撞力；c为变形深度；w 为车身宽度.该式表示车身变形宽度从wn－1到wn，变形深度从cn－1到cn时车身吸收的能量为En.

结合前期研究的车辆的碰撞速度和车体残余变形之间的线性关系，得出车身变形幅度从wn－1，cn－1到wn，cn的等效速度损失vn为

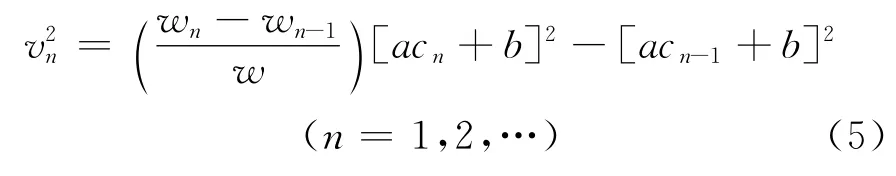
式中：a，b为车辆的刚度系数.

通过式（4）～（5）可以得出车辆与固定物碰撞后瞬间运动量计算模型，结合车辆运动力学计算模型（含轮胎模型理论），得到车辆碰撞固定物的精细计算模型系统［6－7］.

5 系统应用案例

针对西安市咸宁西路兴庆公园南门的一起汽车碰撞路侧固定物（灯杆和树）的交通事故，采用“汽车与路侧固定物碰撞道路交通事故分析计算与再现系统”，进行汽车与路侧固定物碰撞道路交通事故实际案例分析.该事故是行驶中的捷达FV7160CIX／CNG 型轿车和路侧灯杆和树发生碰撞事故，是典型的汽车碰撞固定物事故.采用“汽车与路侧固定物碰撞道路交通事故分析计算与再现系统”对该事故进行分析能够得到事故发生前和事故发生后的相关数据和事故过程，以此为依据来进行该事故的原因和过程鉴定.

首先，将现场采集的数据输入到“汽车与路侧固定物碰撞道路交通事故分析计算与再现系统”，数据主要包括路侧固定物种类与形状、事故车辆碰撞位置与最终停止位置、车体上碰撞痕迹位置、地面制动印迹等道路交通事故现场痕迹数据以及事故车辆的主要结构参数.然后，经过系统绘图和计算得出该事故案例计算过程和结果（如图3），通过图3读取汽车与固定物碰撞前瞬时速度和汽车在驾驶员采取制动措施时的行驶速度.根据系统计算出来的结果，可以对事故发生的原因、过程和结果进行描述，从而进行事故鉴定.采用“汽车与路侧固定物碰撞道路交通事故分析计算与再现系统”可进行类似事故案例的分析计算和再现.

图3 案例计算过程及结果

6 结束语

本研究在收集汽车碰撞固定物相关典型案例基础上，采用车辆动力学，弹性力学和有限元方法的理论，进行了汽车碰撞路侧固定物道路交通事故精细计算与模拟再现技术的理论模型研究.在VC＋＋平台上建立了汽车碰撞固定物的事故现场数据库，开发完成了“汽车与路侧固定物碰撞道路交通事故分析计算与再现系统”.并采用该系统对实际案例进行了分析得到事故现场图和数据，实现了该系统的应用对汽车碰撞固定物事故的鉴定有重要的应用价值.

［1］公安部交通管理科学研究所.GA／T643－2006典型交通事故形态车辆行驶速度技术鉴定［S］.北京：中华人民共和国公安部交通管理科学研究所，2006.

［2］张晓云，金先龙，张淑敏.有限元方法在汽车碰撞事故再现中的应用展望［J］.农业机械学报，2004，35（6）：206－210.

［3］毛娟娟.客车与半刚性护栏碰撞的有限元分析与模拟［D］.大连：大连理工大学，2008.

［4］何宏宇，冯 浩.车辆碰撞护栏事故车速分析的方法［J］.中国司法鉴定，2009（5）：43－45.

［5］左 旭，卫原平.三维六面体有限元网格自动划分中的一种单元转换优化算法［J］.计算力学学报，1999，16（3）：343－348.

［6］魏 朗，陈 涛，余 强.道路交通事故模拟再现的车辆动力学三维模型［J］.交通运输工程学报，2003，3（3）：88－92.

［6］魏 朗.用于碰撞事故中车辆动力学模拟的轮胎模型分析［J］.西安公路交通大学学报，1999，19（1）：73－76.

［7］魏 朗，陈荫三，石川博敏，等.含第二次碰撞的车对车碰撞事故模拟计算模型研究［J］.汽车工程，2000，22（1）：38－41.