钢板浅圆仓屈曲有限元分析
2012-06-15莹尚豫才
杨 莹尚豫才
1.河南工业大学 450001 2.河南工业大学土木建筑学院 450001
钢板浅圆仓屈曲有限元分析
杨 莹1尚豫才2
1.河南工业大学 450001 2.河南工业大学土木建筑学院 450001
本文以工程实际(哈尔滨北仓粮食仓储工程设备有限公司提供的BC2425大豆原料保温钢板筒仓)为载体,利用通用有限元软件ANSYS对该仓在空仓、满仓两种工况下进行模拟,总结得出钢板仓屈曲的变化形式,并对仓底的“象腿”变化给出解释,以及提出钢板浅圆仓避免屈曲破坏的解决措施,并利用理论计算证明有限元模拟的正确性。
钢板浅圆仓;屈曲;有限元分析;等效应力值
筒仓结构是广泛应用于矿业、冶金、建材、化工、电力、建材、粮食等领域的粒状、散状、液状物料储备的一种特殊结构形式的筒状构筑物[1]。近年来,随着我国钢材产量和质量迅速提高,散料储存需求量的不断提高,钢板筒仓的需求量及容量都在迅速增加。由于我国对钢板筒仓受力性能的研究起步较晚,相对较弱,且圆形钢板筒仓是一种旋转薄壳结构,其受力行为、破坏准则等相当复杂,再加上一些不合理的设计准则导致了许多钢板筒仓的结构破坏,许多问题仍有待进一步解决。加之,钢板筒仓属于圆柱薄壳结构,这类结构在外荷载作用下,对其进行承载力及稳定设计研究主要取决于对其进行的屈曲分析。
1 圆柱壳弹性理论公式与规范计算公式
1.1 圆柱壳弹性理论公式
假定圆柱壳为薄壳,径向挠度很小,材料均匀同性,且符合胡克定律、直法线假设,横截面的荷载均匀分布,在两端的边界条件为无径向位移和切向位移,则可以得出圆柱壳的理论解为[2]
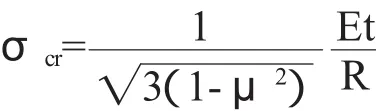
式中,E为材料的弹性模量;t为壳的厚度;R为圆柱壳的半径;μ为泊松比。
1.2 《粮食钢板筒仓设计规范》(GB50322-2001)中的仓壁稳定计算公式
据《粮食钢板筒仓设计规范》(GB50322-2001)[3]之5.3.7条规定,仓壁应按薄壳弹性稳定理论或下述方法进行稳定计算:
1.2.1 在竖向轴力作用下(空仓)的计算公式为
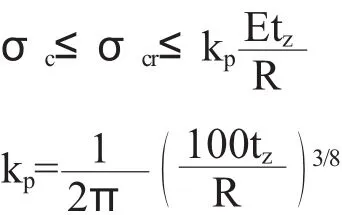
1.2.2 在竖向压力及储粮水平压力共同作用下(满仓)的计算公式为
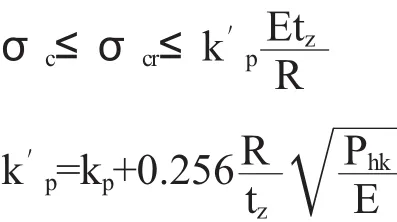
2 钢板浅圆仓BC2425工程概况
2.1 仓储物料的基础物理参数
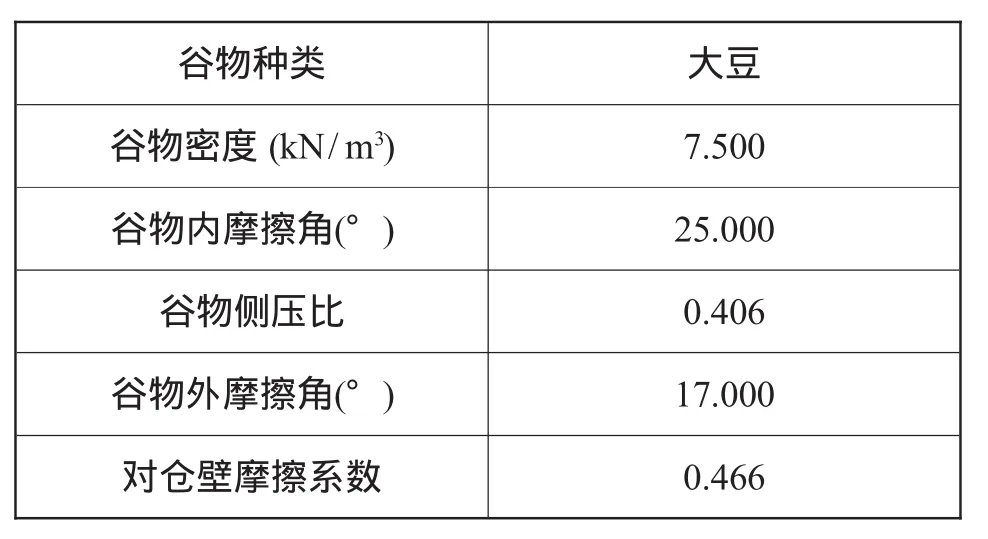
谷物种类 大豆谷物密度(kN/m3) 7.500谷物内摩擦角(°) 25.000谷物侧压比 0.406谷物外摩擦角(°) 17.000对仓壁摩擦系数 0.466
2.2 钢板浅圆仓的基本设计条件

仓身自重(kN) 1580.000仓深(m) 28.500直径(m) 24.000仓壁周长(m) 75.398水力半径(m) 6.000仓体立柱数(个) 72.000仓盖自重(kN) 210.00仓盖投影面积(m2) 498.759仓壁分段(层) 25
2.3 主要构件的材料及其强度

仓壁板材料:Q 3 4 5强度设计值(N/m m 2) 3 0 0.0 0 0内立柱材料:S G H 4 4 0强度设计值(N/m m 2) 3 0 0.0 0 0
3 有限元计算模型
该钢板浅圆仓是由加劲肋和钢板组成,钢板与钢板之间由高强螺栓连接而成。根据钢板浅圆仓BC2425的原始数据,利用通用有限元软件ANSYS进行建模。钢板仓仓壁采用Shelll81板壳单元,加劲肋采用Beaml88梁单元。为了简化模型,在进行结构内力分析时,可以把顶盖和基础模拟为仓壁上下两端的边界约束条件,所以在实际建模时不构建仓顶盖和基础的有限元模型。根据实际情况,将边界条件定位仓顶铰接,仓底固结。根据统计,模型单元数和节点数分别为:12 085个单元和4 868个节点,模型如图1所示。

图1有限元模型
4 计算结果分析
通过有限元后处理得出该模型在空仓、满仓两种工况下的等效应力图与屈曲模态图,分别见图2,图3、图4、图5。从屈曲分析结果看,因结构的特殊性,其屈曲形式出现沿高度方向呈正弦特征的变形曲线,同时沿仓壁的四周有不同的层数。虽然目前在工程设计中还很少采用屈曲分析结果来作为控制筒仓的设计要素,但是,为了防止筒仓屈曲失稳,建议适当加强加劲肋沿径向和环向的抗弯刚度或加大仓壁的厚度。

图2空仓荷载作用下等效应力图

图3满仓荷载作用下等效应力图
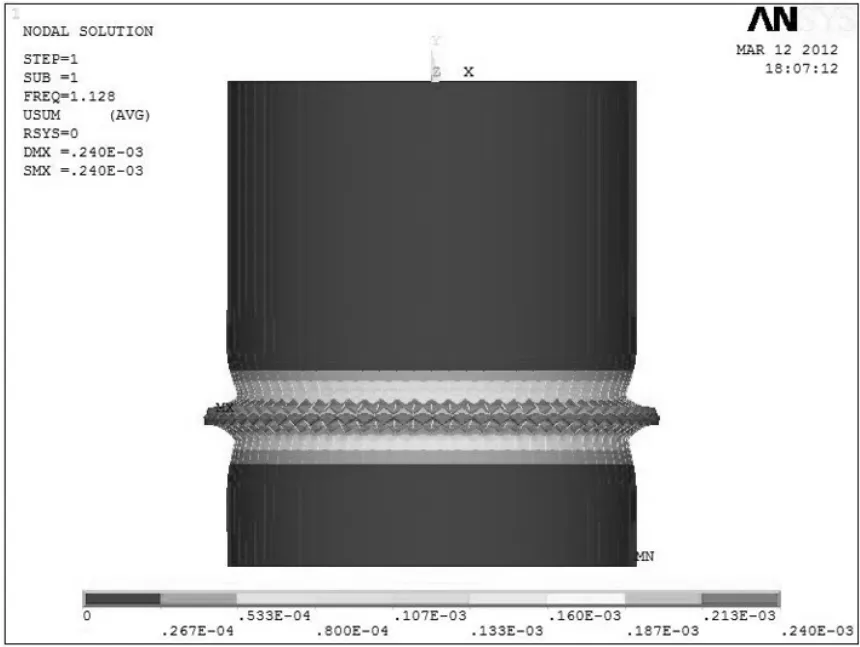
图4空仓荷载作用下屈曲模态图

图5满仓荷载作用下屈曲模态图
图4和图5都出现了“象脚”变形。这是因为筒仓底部固结,其径向、环向变形受到约束。在空仓状态下,仓壁只受竖向力的作用,使接近于仓底部分的仓壁环向变形很大;在实仓状态下,仓壁不仅受竖向力的作用,还受粮食水平力的作用,使得其环向变形比空仓状态时小,所以在实仓状态下的“象脚”效应比空仓状态下的小。从空仓和实仓屈曲模态图的形状上来看,与袁海龙在《粮食钢板筒仓整体稳定设计综述》[4]一文中所得的结论相一致。
5 有限元模型验证
通过有限元分析计算,选取满仓工况下第一特征屈曲模态图,其特征值屈曲荷载为F=615912kN。根据圆柱壳在轴压作用下的临界荷载值计算公式算得:

式中参数都是根据实际情况取得,通过比较可以看出:有限元分析值和理论计算值仅相差0.4%,故验证所选取的单元类型、网格划分大小和对筒仓的施加约束均合适对该类筒仓做有限元分析。
6 结论
从屈曲分析结果看,钢板浅圆仓屈曲形式为沿高度方向呈正弦特征的变形,同时沿仓壁的四周有不同的层数。为了防止筒仓屈曲失稳,建议适当加强立柱沿径向及环向的抗弯刚度或增大仓壁的厚度。在实际工程中,应在筒仓底部采取必要的构造措施来避免“象脚”效应的发生。
[1]段亚弟,申跃奎.贮仓结构抗震研究的综述[J].清华大学;第六届全国土木工程研究生学术论坛,2008
[2]王新敏.ANSYS工程结构数值分析 [M].北京:人民交通出版社,2007.
[3]郑州粮油食品工程建筑设计院.GB50322-2001粮食钢板筒仓设计规范[S].北京:中国计划出版社,2001.
[4]袁海龙.粮食钢板筒仓整体稳定设计综述 [J].特种结构,2008(8):21-24.
杨莹,女,1982年5月出生,四川乐山人,硕士,助理工程师。)
