基于模糊函数的脉冲信号检测技术

赵 研，苑 蕾，霍 达

(中国电子科技集团公司第五十四研究所，河北石家庄050081)

0 引言

时频变换作为一种信号处理手段，具有优良的时频域分辨特性，能够满足时、频二维对信号的分离，有一定多信号处理的能力，作为时频支撑集而具有聚集性，此外还有其他很多优点。

广大研究人员对威格纳崴利(WVD)进行了深入分析和讨论。比如在二次型分布对于非平稳信号的检测性能、WVD对线性调频脉冲信号的分析性能、时频分析的脉内调试识别、多信号分量的二次型分析、核函数滤波[1]等都取得了许多的研究成果。但一般对于Cohen类[2]的模糊函数在电子侦察领域关注得较少，而模糊函数研究也都是传统雷达信号处理中的匹配信号处理思路对其展开研究，WVD对白噪声中的信号具有良好的检测能力。由于二次型分布具有表现信号瞬时功率谱密度的能力，因此在二次型分布中讨论信号的检测与识别，很大程度是对信号的瞬时功率谱密度的特性分析。根据物理能量准则，依据信号和噪声能量在特定时频域中强弱分布的先验知识，有效地分离噪声和感兴趣的信号，从而再进行信号检测，无疑是一种趋于最优的方法。

1 模糊函数基本理论

1.1 时频分析原理

在信号分析领域中，时间和频率是最基本、最常用、最方便的度量子空间，信号的相关函数和功率谱是这2个子空间中最常用的物理测度。在非平稳信号分析中，传统的傅里叶变换受到了限制，因为非平稳信号的频率成分是时变的，相关函数和功率谱等统计量也是时变函数，这时只了解信号的全局特性是远远不够的，需要获得信号的频谱随时间变化的特征以及信号的时频局部化特征，所以分析非平稳信号要用时间和频率的联合函数来表示。虽然认为信号本身是全局非平稳的，但是在具体局部域却是近似平稳的。这种表示称为信号的时频表示，基于信号时频表示的信号分析称为信号的时频分析。

1.2 脉冲信号的模糊函数

在脉冲信号处理中，模糊函数是一种信号分析与设计的重要工具。当目标被视为“点”目标时，回波信号的波形与发射波形相同，但有不同的时延τ和ξ不同的频偏(多普勒频率)，此时的输出脉冲模糊函数为该信号匹配滤波输出对τ、ξ的二维响应。

在非平稳信号处理中，模糊函数采用不同的定义:对瞬时自相关函数做关于t的傅里叶反变换而不是傅里叶变换。即定义为:

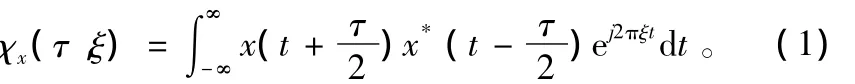
模糊函数也可以用信号的傅里叶变换X(f)定义为:

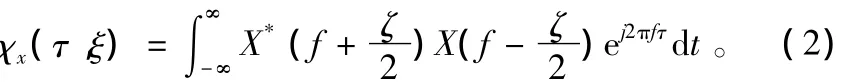
脉冲信号具有多种多样的功能和用途，与之相对应的有各不相同的信号形式(不同的模糊函数特征)。随着综合射频技术及体制的发展，根据不同用途和功能出现了类型繁多、特征各异的综合射频脉冲信号，如从频率域的信号形式来看，基本可以将这类信号分为:单频脉冲信号、调频脉冲信号、调相脉冲信号、频率编码脉冲信号和频率分集脉冲信号等[3]。

2 模糊距离空间

如果将截获的脉冲信号时频截段投入到L2空间(L2是线性空间)中，若使用内积定义，设=(x1，y1)=(x2，y2)均为单位矢量，是空间内的任意2个向量，定义:

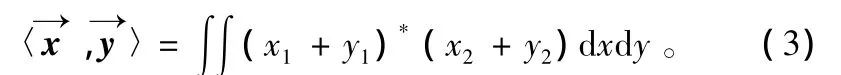
显然式(2)满足内积公理[4，5]，则可成内积空间。由模糊函数的共轭对称性质可推知，当为模糊函数时，内积〈，〉为实数，则有≥0。可知此时信号内积空间同时满足距离的定义，即

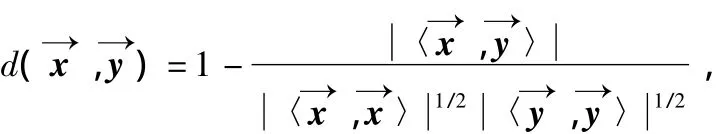
构成距离空间。

基于投影定理(Projection Theorem)[6]得到内积〈〉是信号在上的投影值。使用上面的结论，投影值此时也是2个信号之间的距离的一种表象，其物理概念为在标准笛卡尔正交基下，2个信号模糊函数的相关性度量(相关性越好，距离越小)。

对于本文的应用来说，模糊域内时延τ和频移ξ构成了L2空间的一组正交基。噪声、各种脉冲信号都具有各自特征的模糊函数，根据截获的信号时频截段而产生的模糊函数与特征模糊函数之间是可以通过相关性(距离)的比对进行判决的。

白噪声模糊函数如图1所示，从图1可以看出二次型分布对于局部平稳的噪声检测具有良好的适应性。在模糊域，对于带内的高斯白噪声，模糊函数有极好的非周期相关性。

图1 白噪声模糊函数

白噪声的模糊函数集中在坐标原点(0，0)及周围，而在广大的平面内少有分布。类似于WVD中的分析，对于某随机信号x(t)=s(t)+n(t)，其中s(t)为解析的确定信号，n(t)是一平稳零均值有色噪声。可知加性噪声下确定信号的模糊函数有:

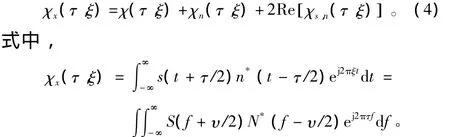
可以证明:χx(τ，ξ)= χs(τ，ξ)+ χn(τ，ξ)。χn(τ，ξ)代表平稳噪声n(t)的模糊函数。若假定噪声是带限白噪声，则上式变为:

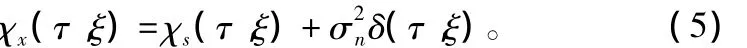
前面提到的空间内积距离的方法原则上是具有检测的能力，但由于噪声具有随机特性，对于使用的噪声模糊函数模板(某特定时间段内的噪声模糊函数)与实际噪声之间的模糊函数相关性，是检验信号检测算法的重要考量。

3 仿真分析

3.1 判决距离仿真分析

通过Matlab仿真工具软件，模拟独立的100次噪声数据截断，与标准噪声模糊函数模板做内积距离估计，得到蒙特卡洛试验结果如图2(a)所示。

从图2(a)可以看出，内积距离结果基本在(0.993，1)区间以内，而相同的噪声模糊函数模板与简单脉冲信号模糊函数之间的内积距离值为0.999 240，二者十分接近。这种结果与预想情况是有明显差距的，究其原因是在内积运算中使用的是复数形式的模糊函数内积。而噪声在独立条件时，其模糊函数的相位是独立的，这反映了噪声的高阶非相关性。所以从内积的结果来看，并没有预想的那样二者内积很小(相似度很高)。这就要对信号检测算法进行改进，以适应噪声的这种特征。

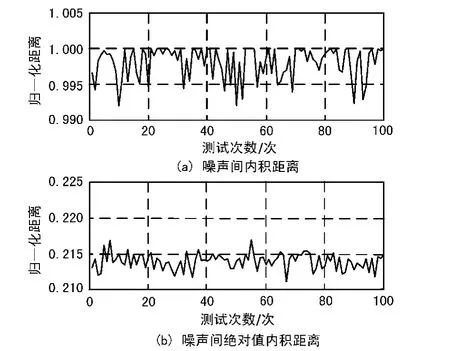
图2 噪声间内积距离测试

由于模糊函数本身具有体积不变的特征，而噪声的模糊函数主要集中于原点附近。于是可以提出基于模糊函数绝对值的内积估计方法，即

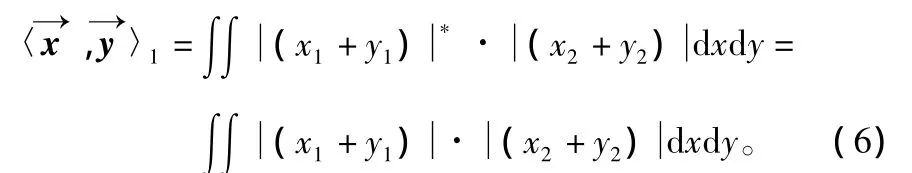
使用绝对值后模糊函数对于相位信息不在敏感，能够对于噪声高阶不平稳性进行一定的滤除。以上面例子中的噪声模拟实验为例，完全相同的数据经过绝对值内积估计后测量值如图2(b)所示，而此时简单脉冲信号与噪声模板模糊函数的绝对值内积估计为0.839 203(典型值)、线性调频为0.846 2(典型值)、二相编码为0.687 9(典型值)，显然这种测算方法优势明显。

3.2 信号检测仿真分析

信号的检测的另一重要考量内容是信号检测所能适应的信噪比，需要考察检测方法受信噪比下降的影响程度，以确定算法处理信号的灵敏度。

对于简单脉冲信号引入加性白噪声(此时噪声可认为是极窄带内或同频噪声)，设置与数据截段长度相适应的噪声信号，控制带内信噪比可得如图3(a)所示绝对值内积距离仿真测量结果。当信噪比大于－10 dB时，信号满足一般门限检测条件。

对相位编码脉冲信号引入加性白噪声(此时噪声可认为是信号带内噪声)，设置与数据截段长度相适应的噪声信号，控制带内信噪比可得如图3(b)所示绝对值内积距离仿真测量结果。当信噪比大于－3 dB时，信号满足一般门限检测条件。

对于线性调频脉冲信号引入加性白噪声(此时噪声可认为是信号带内噪声)，设置与数据截段长度相适应的噪声信号，控制带内信噪比可得如图3(c)所示绝对值内积距离仿真测量结果。当信噪比大于－11 dB时，信号满足一般门限检测条件。

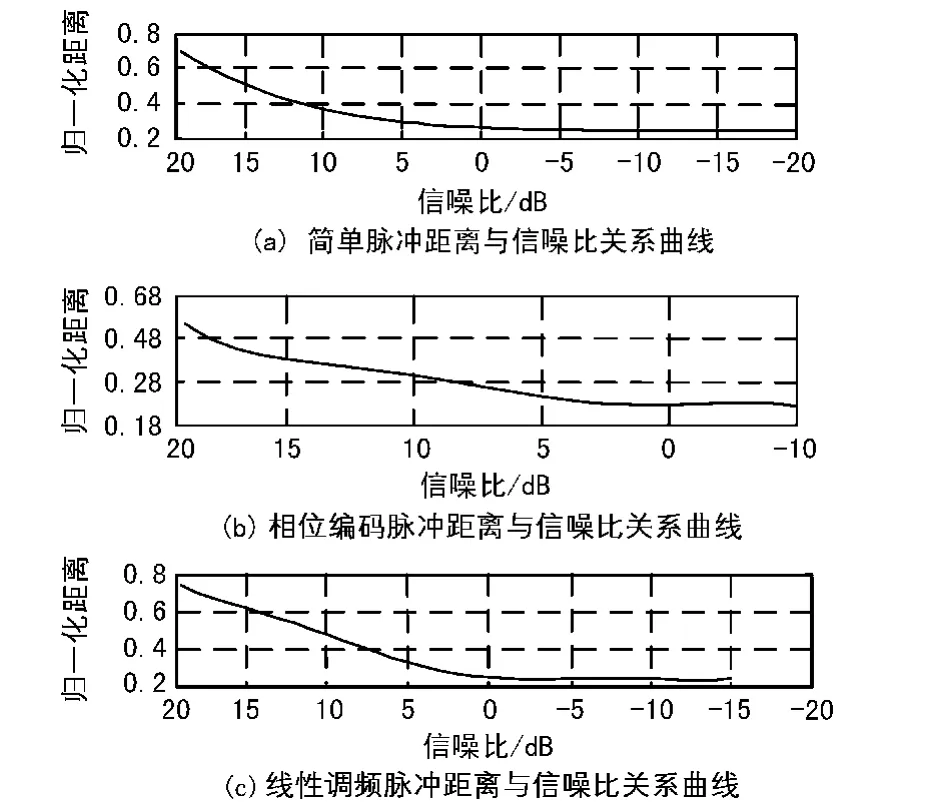
图3 各种脉冲信号距离与信噪比关系曲线

以上分析说明取得这种效果的根本原因是利用了噪声在能量域中的二阶统计特征，这是在常规处理中一般难以取得的。

对于本文的分析来说，噪声、各种脉冲信号都具有各自特征的模糊函数，根据截获的信号时频片段而产生的模糊函数与特征模糊函数之间是可以通过相关性(距离)的比对进行判决的。这种处理思路有2点理论上的缺陷:

①由于样本空间的非稠密性而使得空间不具有完备性，距离不具有绝对的收敛性。简而言之是信号模糊样本不具有针对空间截获信号截段的全部本质表达，存在漏项，因而依据距离的判断归类是不严格准确的。

②由于模糊函数是对信号二阶统计量(相关函数)的处理，对于二阶统计不平稳的信号，如加性噪声等敏感。所以处理算法对于这类信号也存在缺陷。

这2种缺陷主要表现为处理方法理论上的不完备性，对实际的工程应用影响不大。

4 结束语

从以上的理论推导以及仿真结果来看，基于模糊域的绝对值内积距离信号检测方法可以在带内或同频噪声中有效地检测微弱信号。对于简单脉冲、相位编码脉冲和线性调频脉冲等信号可分别在信噪比－10 dB、－3 dB和－11 dB条件下实现信号的检测，该性能指标优于一般处理方法，具有较好的工程应用潜力。在后续开发中需要关注该方法的计算量优化和硬件设计实现等技术。

[1]JEONG J.WILLIAMS W J.Kernel Design for Reduced Interference Distributions[J].IEEE Trans Signal，1992，40(2):402－412.

[2]C OHEN L.POSH T E.Generalized Ambiguous Function[J].Pro IEEE Cof On ASSP，Tampa，1985，27(3):61 －64.

[3]RICHARDS M A.雷达信号处理基础[M].邢孟到，译.北京:电子工业出版社，2008:117－164.

[4]汪学刚，张明友.现代信号理论[M].北京:电子工业出版社，2005:28 －52.

[5]宋国乡，冯有钱.数值分析[M].西安:西安电子科技大学出版社，2002:4－11.

[6]SERGIOS T.模式识别[M].李晶姣，译.北京:电子工业出版社，2006:1－41.