模拟滤波器群时延及驻波比的优化设计

李 鹏,张 丹,马红梅

(华北科技学院 电信系,北京 101601)

模拟滤波器群时延及驻波比的优化设计

李 鹏,张 丹,马红梅

(华北科技学院 电信系,北京 101601)

针对网络综合方法不能直接对滤波器的群时延和驻波比同时设计的问题,提出了一种滤波器的幅频特性、群时延和驻波比特性同时优化的设计方法,即在网络综合法设计滤波电路的基础上,利用无约束优化方法对群时延和驻波比同时优化,降低通带内群时延波动和驻波比的最大值。从仿真结果可以看出,优化后滤波器幅频特性接近算术对称,群时延波动最大值17.337 ns,驻波比最大值仅为1.455 0。

模拟滤波器;幅频特性;群时延;驻波比;算术对称;优化设计

1 引 言

滤波器是电子、通信系统中最常用的器件,随着现代电子技术的不断发展,对滤波器的小型化、集成化也提出了越来越高的要求[1]。滤波器的设计一般采用网络综合设计方法,但该方法只能针对滤波器的幅频特性进行设计,而且设计出的滤波器幅频特性是在对数坐标下对称,而不是实际应用中的线性坐标系下对称。另外,网络综合设计方法也不能分别针对滤波器的群时延特性和驻波比进行设计,更不能同时对群时延特性和驻波比进行设计[2]。

本文是利用优化的设计方法,将滤波器的幅频特性、群时延特性和驻波比同时进行优化,以使综合指标达到各个指标的最佳值。作者在文献[2]中提出了应用极点放置技术的幅频算术对称滤波器的优化设计方法,该方法的主旨是利用极点放置技术和优化技术使滤波器的幅频特性在算术坐标下对称。文献[3]中提出了滤波器群时延内均衡优化设计方法,即将网络综合法设计的滤波器电路与时延均衡器直接耦合,用最小二乘法使群时延特性逼近一个常数,然后利用无约束优化算法对整个电路进行优化来降低通带内群时延波动。文献[4]中提出了一种改进电路的滤波器驻波比优化设计方法,利用电路优化技术使得幅频特性在线性坐标下对称且通带内驻波比接近于1。

在本设计中,因为不改变滤波器的结构和元件个数,只是将初始元件参数进行优化,从而得到更加理想的元件参数,因此存在着滤波器的幅频特性、群时延特性和驻波比这3个性能指标互相矛盾的问题。如何在通带内得到较好的群时延特性和较小的驻波比波动,同时在阻带获得较大的衰减使滤波器的这3个性能指标能够同时达到合理的平衡,是本文设计的重点和难点。本文先利用极点放置技术和优化方法使滤波器的幅频特性在线性坐标下对称,然后再直接耦合时延均衡器,利用最小二乘法使群时延特性逼近常数,再对电路进行整体优化使3个指标都能达到一个合理的平衡。

本文设计的滤波器集线性坐标对称的幅频特性、线性的群时延特性和较小的驻波比于一体,可以减小滤波器的体积,减少元件个数,不需要增加额外的器件,减小损耗,降低制造成本,且电路阶数少、结构简单[2]。

2 滤波器总目标函数数学模型的建立

滤波器总的目标函数就是幅频特性目标函数、群时延特性目标函数与驻波比特性目标函数的代数和。滤波器幅频特性和群时延特性的数学模型的建立参见文献[3],滤波器驻波比特性的数学模型的建立见文献[4]。

2.1 滤波器总目标函数的建立

对幅频特性、群时延特性和驻波比特性的优化过程中,先在通带和阻带取若干个频率点,幅频特性是共取m个频率点,然后求输出电压的实际值与理想值之差的平方和[2]。在通带取p个频率点,然后求驻波比与理想值1的差之和,再求群时延的实际值与理想值之差的平方和,所以总的目标函数一般可以写成

式中,Vo(X,ωi)是由节点电压法求出的输出电压实际值; Vo(ωi)是输出电压理想值,其值是已知的[2];γ(X,ωk)为各频率点上的驻波比,其值的求得可以参见文献[4];τ(X,ωk)为各个频率点上由相位求导得到的实际的群时延值;C为理想的群时延特性曲线,其值为一常数[5],求解方法可以见文献[3];W1(ωi)是幅频特性的权重函数,W2(ωk)为相频特性的权重函数,Wγ(ωk)为驻波比特性的权重函数,在优化的过程中权重函数可以任意调节。

2.2 总目标函数的梯度

利用无约束优化方法进行优化时,首先就要求出总目标函数的梯度,总目标函数的梯度就是滤波器的驻波比、群时延和幅频特性对元件的灵敏度的代数和。要求出目标函数对每个元件的灵敏度,对幅频特性的梯度,可以参见文献[2],对于驻波比特性的梯度,可以参见文献[4],对群时延特性的梯度,可以参见文献[3],其可以由下式求得:

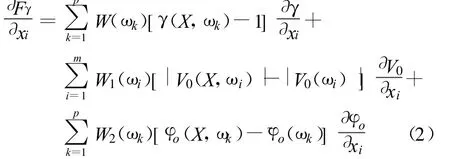
3 滤波器的优化

在优化的过程中,需要对滤波器进行反复优化才能得到合理的元件参数值。首先要利用无约束优化方法对网络综合设计方法得到的滤波器的幅频特性进行优化,使滤波器的幅频特性在线性坐标下接近于算术对称。然后,在此电路上直接耦合时延均衡器,再用最小二乘法对滤波器的群时延特性进行优化,使群时延接近于一条直线。最后,再利用无约束优化方法对整个滤波器进行优化,此时要不断地调整各个频率点的权重函数,使幅频特性、群时延特性和驻波比特性3个指标综合达到一个最佳的合理的平衡点。

本文所采用的无约束优化方法的实质是采用修正的BFGS方法与填充函数法相结合,反复对目标函数进行优化,直到3个性能指标都满足设计要求,即得到全局最优解为止。无约束优化方法即先用修正的BFGS方法求出总目标函数的一个局部最优解X＊,然后以局部最优解X＊构造填充函数,接着再用修正的BFGS方法求出填充函数的新的局部最优解X′,接着再以X′为初始点求出F(X)的局部最优解,此解如果不是全局最优,那么再构造填充函数,如此多次反复,直至得到全局最优解[6]。

具体优化步骤如下:

步骤1:根据滤波器设计指标利用网络综合设计方法确定滤波器原型并计算出滤波器元件参数的初始值;

步骤2:取若干频率点根据公式(1)得到滤波器的幅频特性、群时延特性和驻波比特性的总目标函数;

步骤3:根据公式(2)采用特勒根伴随网络求出总目标函数的梯度;

步骤4:利用修正的BFGS方法对目标函数进行优化,优化的过程不断调整各个频率点的权函数,直到得到一个局部最优解X＊;

步骤5:以局部最优解X＊构造填充函数,接着再用修正的BFGS方法求出填充函数的新的局部最优解 X′;

步骤6:判断此解是否为全局最优或者是否符合滤波器的指标要求,如符合要求则解X′为最优解,优化完成;

步骤7:如此解不是全局最优或者不符合滤波器的指标要求,则以X′为初始点返回步骤2。

4 实例分析

本设计所用的实例采用文献[3]的电路,要求中心频率是490MHz,3 dB带宽为70 MHz,线性坐标下±90MHz处衰减大于55 dB,矩形系数小于2.5,群时延波动小于20 ns,线性坐标下490±35 MHz内驻波比要小于1.5,两端接电阻都是50 Ψ。

该滤波器采用6阶电容耦合谐振滤波器作为设计原型得到滤波器的结构及元件参数[7],利用极点放置技术放置极点后再优化使幅频特性在线性坐标下对称。然后改进电路后耦合时延均衡器,再利用最小二乘法和无约束优化方法使群时延特性接近于一条直线[8]。此时滤波器的幅频特性和群时延特性已经符合要求,具体曲线见文献[3],但是驻波比很大,滤波器电路图和驻波比特性曲线分别如图1和图2所示。

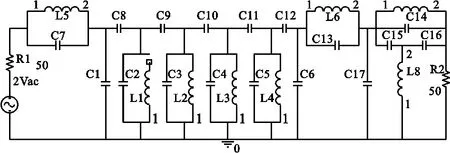
图1 时延均衡器直接耦合电路Fig.1 Filter circuit coupledwith group-delay equalizer

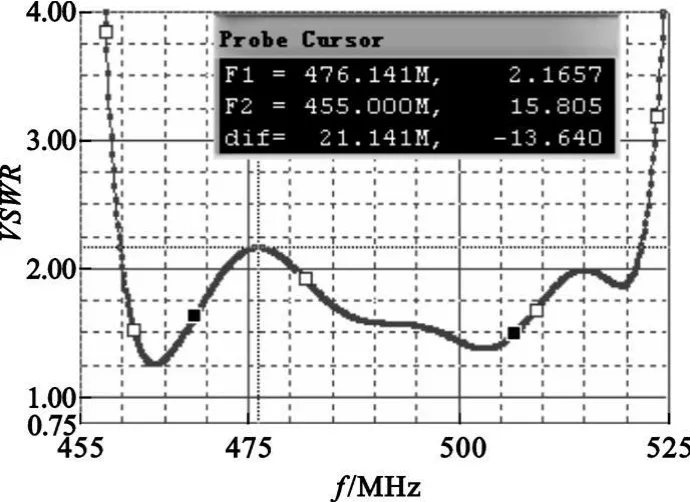
图2 优化前的驻波比特性Fig.2 VSWR before optimization

从仿真图可以看出,此时滤波器驻波比波动的最大值为2.165 7。为降低驻波比的波动,再利用无约束最优化方法对电路进行优化,在优化的同时调整各个权重函数,最后得到优化后的滤波器的幅频特性、群时延和驻波比特性[9]。优化后的滤波器的幅频特性、群时延和驻波比特性如图3、图4和图5所示。

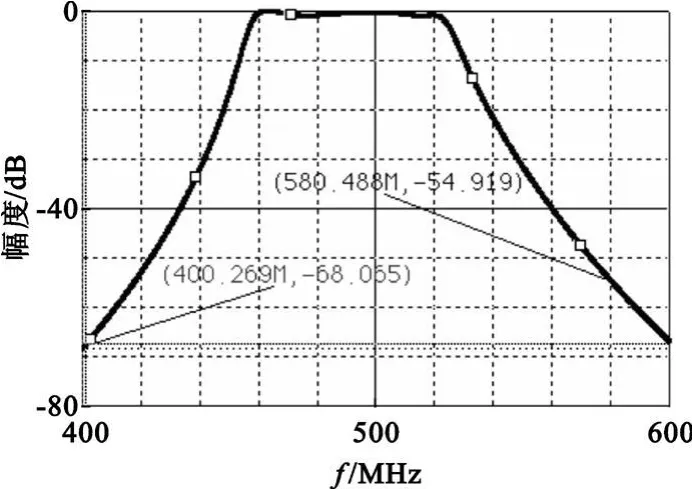
图3 优化后的幅频特性Fig.3 Amplitude-frequency after optimization

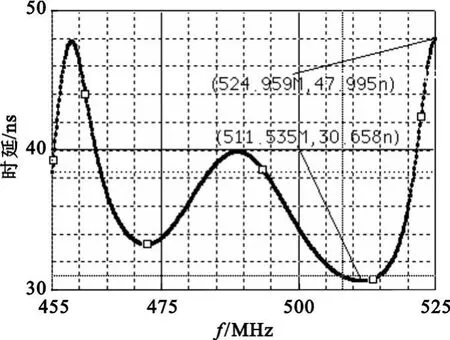
图4 优化后的群时延特性Fig.4 Group-delay after optimization

由仿真可以得出,幅频特性基本能够达到线性坐标下对称,在 490±90MHz处的衰减分别为68.055 dB和54.919 dB,通带内群时延的最大波动为17.337 ns,而滤波器的驻波比波动的最大值由优化前的2.165 7降低到了优化后的1.455 0。

5 结 论

本文利用网络综合法设计的滤波器内接时延均衡器,再进行整体优化,使滤波器的幅频特性、群时延和驻波比特性能够实现合理的折衷。由于电路的结构并没有改变,只是将滤波器元件参数进行了优化,所以滤波器的3个指标之间本身存在着的固有矛盾,因此只能通过在这3个指标中找到一个最佳的平衡点得以解决。

对比仿真曲线可以看出,滤波器幅频特性的阻带抑制在高频端小于文献[2]的阻带抑制,所以幅频特性的对称性相比于文献[2]要差一些。相对于文献[3],通带内群时延的最大波动由10.977 ns增大到17.337 ns,而驻波比波动的最大值由优化前的2.165 7降低到了优化后的1.455 0。

设计实例表明,优化设计方法相对于网络综合设计方法来说,在不改变滤波器结构的情况下,利用优化技术不但能够使滤波器的幅频特性、驻波比特性和群时延特性达到一个合理的折衷,而且能够解决网络综合设计方法难以解决的驻波比和线性群时延设计上相互矛盾的问题,并且具有良好的工程应用价值。

本设计只是在理论上解决了滤波器的幅频特性、群时延和驻波比特性的同时设计问题,在实际的制作中还要考虑电容和电感的精确取值问题、焊点的杂散电容问题、引线的线间电容和电感问题等。

[1]王大寿,赵涛.LC滤波器的小型化制作与生产[J].大连海运学院学报,1994,20(4):60-66.

WANG Da-shou,ZHAO Tao.The miniaturization make of the LC filters[J].Journal of DalianMarine College,1994,20(4):60-66.(in Chinese)

[2]李鹏,马红梅.幅频算术对称无源带通滤波器的优化设计[J].电讯技术,2010,50(6):105-108.

LI Peng,MA Hong-mei.Optimization Design of Amplitude-frequency Arithmetic Symmetry Passive Bandpass Filter[J].Telecommunication Engineering,2010,50(6):105-108.(in Chinese)

[3]李鹏,马红梅.群时延内均衡的模拟滤波器优化设计[J].电讯技术,2011,51(5):99-103.

LI Peng,MA Hong-mei.Optimization Design of Analog Filter′s Group-delay Inner Equalized[J].Telecommunication Engineering,2011,51(5):99-103.(in Chinese)

[4]马红梅,李鹏.UFH频段超带宽模拟滤波器驻波比的优化设计[J].电讯技术,2011,51(6):138-141.

MA Hong-mei,LI Peng.Optimization Design of the UFHBand UWB Analog Filter′s VSWR[J].Telecommunication Engineering,2011,51(6):138-141.(in Chinese)

[5]沙海.卫星导航系统传输信道的群时延测量方法研究与应用[D].长沙:国防科技大学,2009.

SHA Hai.Research and Application of theGroup Delay Measurement Method in Transfer Channel of Satellite Navigation System[D].Changsha:National University of Defense Technology,2009.(in Chinese)

[6]邓振坤,姜爱萍,濮定国.求解无约束全局优化问题的一种方法[J].内蒙古师范大学学报(自然科学汉文版),2008,37(1):6-10.

DENG Zhen-kun,JIANG Ai-ping,PU Ding-guo.A Method for UnconstrainedGlobalOptimization[J].Journalof Inner Mongolia Normal University(NaturalScience Edition),2008,37(1):6-10.(in Chinese)

[7]Williams A B.电子滤波器设计手册[M].喻春轩,译.北京:电子工业出版社,1986:201-208.

Williams A B.Design Handbook of Electric Filter[M].Translated by YU Chun-xuan.Beijing:Publish House of Electronics Industry,1986:201-208.(in Chinese)

[8]张天良,羊恺,孔根升,等.高温超导小型化交叉线自均衡线性相位滤波器[J].科学通报,2010,55(15):1453-1458.

ZHANG Tian-liang,YANG Kai,KONG Gen-sheng,et al.Miniature linear-phase superconducting filter with group delay equalization[J].Chinese Science Bulletin,2010,55(15):1453-1458.(in Chinese)

[9]谢勇,赵文华,薛军.测控站高功放电压驻波比自动检测系统的实现[J].电讯技术,2008,48(3):100-103.

XIE Yong,ZHAO Wen-hua,XUE Jun.Implementation of an Automatic VSWR Detection System for the High Power Amplifier(HPA)of a TT&C Station[J].Telecommunication Engineering,2010,48(3):100-103.(in Chinese)

LI Peng was born in Chifeng,Inner Mongolia Autonomous Region,in 1974.He received the M.S degree from Dalian Marine U-niversity in 2006.He is now a lecturer.His research interests include circuit and system and signal processing.

Email:lp031006@163.com

张 丹(1984—),女,助教,主要研究方向为计算机控制;

ZHANG Dan was born in 1984.She is now a teaching assistant.Her research concerns circuit and system.

马红梅(1975—),女,内蒙古赤峰人,现为讲师,主要研究方向为电路与系统。

MA Hong-mei was born in Chifeng,Inner Mongolia Autonomous Region,in 1975.She is now a lecturer.Her research interests include circuit and system.

Optimization Design of Analog Filter′s Group-delay and VSWR

LI Peng,ZHANGDan,MA Hong-mei
(Department of Telecommunication,North China Institute of Science and Technology,Beijing 101601,China)

For the problem that an analog filter′s group-delay and voltage standing-wave ratio(VSWR)can not be designed simultaneously by the network synthesis method,an optimal design method for amplitude-frequency characteristic,group-delay andVSWR is proposed.Based on design of filter circuit by network synthesis method,the unconstrained optimization method is used to opitmize the group-delay and the VSWR simultaneously to reduce the group-delay ripple and the max value of VSWR.The simulation results show that the proposed method can get arithmetic symmetrical amplitude-frequency,the max value of VSWR is only 1.455 0 and the group-delay ripple is 17.337 ns in pass-band.

analog filter;amplitude-frequency characteristic;group-delay;VSWR;arithmetic symmetry;optimization design

TN713

A

10.3969/j.issn.1001-893x.2012.06.030

1001-893X(2012)06-0979-05

2011-12-02;

2012-03-02

河北省教育厅科学研究基金资助项目(Z2006439);华北科技学院基本科研基金项目(DX1207B)

Foudnation Item:The Natural Science Foundation of Hebei Educational Commission(No.2006439);The North China Institute of Science and Technology Foundation(DX1207B)

李 鹏(1974—),男,内蒙古赤峰人,2006年于大连海事大学获电路与系统专业硕士学位,现为讲师,主要研究方向为电路与系统及信号处理;