扩频测控信号抗干扰性能评价方法研究

孟生云,杨文革

(装备学院测控工程研究中心,北京 101416)

扩频测控信号抗干扰性能评价方法研究

孟生云,杨文革

(装备学院测控工程研究中心,北京 101416)

在分析有源干扰机理和扩频测控信号处理原理的基础上,提出以基于模糊图的有效面积和一定高度下切割面积评价扩频测控信号固有抗干扰性能的方法。模糊图的有效面积和切割面积越小,则扩频测控信号的固有抗干扰性能越强。仿真示例表明,所提面积指标均可有效反映信号固有抗干扰性能。该方法具有可计算性,可为扩频测控信号的抗干扰性能评价提供方法依据。

测控系统;扩频信号;固有抗干扰性能;模糊函数

1 引 言

空间电子对抗理论与技术的不断发展要求空间信息平台的测控系统应具备较强抗干扰能力。抗干扰测控系统的研究与开发已成为我国测控界关注的重点之一,如已走向实用的直扩统一测控系统,以及近年来提出的抗干扰测控体制如基于混沌扩频技术[1]、基于直扩/跳频混扩技术[2]、基于多载波技术[3]等。

对扩频测控系统的抗干扰性能分析主要集中于分析系统的信息传输功能的抗干扰性能[4],未见文献从信号自身特征的角度考察扩频测控信号抗干扰性能。文献[5]从模糊函数的角度提出了引信的固有抗干扰性能评价方法。受其启发,本文从信号自身特性出发,研究了扩频测控信号固有抗干扰性能的评价问题。

模糊函数[6]反映了信号在时延-多普勒频移二维联合域中的分辨情况。扩频测控系统完成信息传输及测量任务的基础均是基于信号相关处理理论。本文以信号模糊分辨特性为纽带,建立了基于模糊图有效面积和切割面积的信号固有抗干扰性能评价指标,给出了仿真实例,分析说明指标的客观合理性。

2 有源干扰机理及模型

航天测控系统通常采用连续波体制,其发射信号为周期信号,但在接收处理过程中是以单周期或整周期的时间长度信号为对象,因此接收处理信号可归属为有限时间信号。

设有限时间信号x(t,·)的集合记为S(TD),可表示为

式中,TD为信号持续时间,α为信号的n维的独立特征参量,A为包括信号时间、频率和空域的独立特征参量的完备矢量集合。

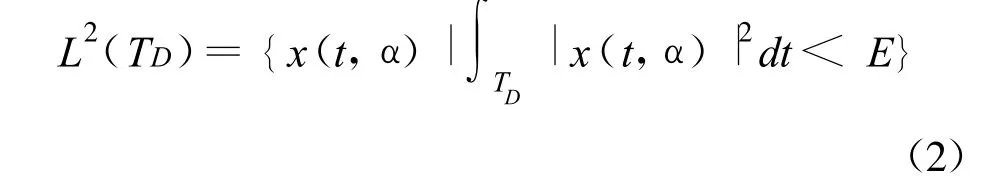
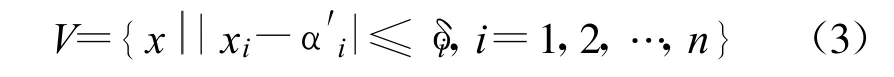
式中,δi为信号特征参量α′i不分辨距离的度量,区域V为接收信号x(t,α′)在特征参量空间 Χ中的不分辨区域,即接收方不能分辨落在区域内的两个参量 α′1、α′2。

若干扰的参量也落在不分辨区域内,则接收方将分辨不了该干扰信号,则对参量 α′的分辨形成了有效干扰,故不分辨域 V也称为干扰有效区域。于是有效干扰条件是干扰的特征参量αJ需要落在接收信号特征参量空间Χ的干扰有效区域V内。

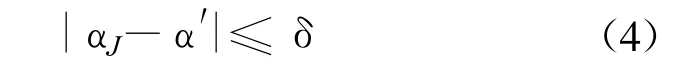
式中,δ为干扰有效区间距离度量的矢量形式。可见距离测度 δ越大即干扰有效区域越大,干扰特征参量越容易进入区域 V,信号就越容易受到干扰,则信号的固有抗干扰性能越弱。图1给出特征参量为二维时的干扰有效区域示意图。干扰aJ(τ′,η′)落在 V外,干扰与信号能分开,干扰aJ(τ,η)落在有效干扰区域V内,干扰与信号不能分开则干扰有效。

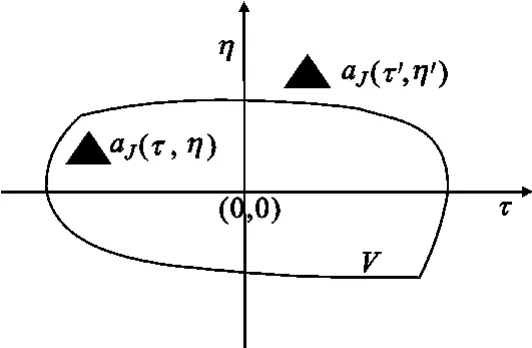
图1 干扰有效区域示意图Fig.1 Effective jamming domain

3 扩频测控信号固有抗干扰性能评价指标

3.1 扩频测控信号处理原理

统一扩频测控系统利用一路载波、一副天线完成对航天器的跟踪测量、遥控遥测和数传的打包传输等任务。在测控系统完成系统捕获基础上,包括天线伺服系统完成角捕获、星上应答机锁定上行信号、地面跟踪接收机锁定下行信号等,地面测控站通过上行信道发送遥控测距信号,星上应答机利用扩频序列良好的相关特性,完成对上行信号的高精度跟踪、解扩解调及时延和多普勒提取,解调出的遥控信息送给执行单元,并将时延多普勒、遥测数传信息通过下行信道转发给地面测控站,地面测控站从下行信号中提取时延和多普勒频移,从而解算出地面站与航天器间的距离和相对速度,同时解调出遥测和数传信息,实时监控航天器自身及运行的状态。

扩频测控系统实现测距测速和遥测遥控等任务均是以信号相关处理为基础,利用了扩频序列良好的二维相关特性。测控系统关注的参量为收发信号间的相对时延和多普勒,故测控信号的特征参量限定为时延和多普勒两维。模糊函数反映了发射信号与带有时延和多普勒频移副本信号间的相关关系,可用于分析信号在时延维和频率维的模糊特性及分辨特性。基于干扰机理的认知,模糊函数在时延-多普勒的主瓣越尖锐,干扰特征参量越难落在主瓣中,此时表明信号特征参量空间避开干扰特征参量的能力越强,则扩频测控信号固有抗干扰性能越好。

3.2 固有抗干扰性能评价指标

式(4)中度量δ是对干扰有效区域各维度距离的度量,不适用于对时延-多普勒联合区域评价。为了便于衡量时延-多普勒联合域的分辨能力或尖锐程度,需要建立能反映干扰有效区域V面积的指标,指标应该遵从联合分辨越好或者模糊图越尖锐指标值越低的原则。本节给出两个衡量信号固有抗干扰性能指标,即模糊图的有效面积和一定高度下的切割面积,两者均在不考虑干扰类型的情况下,从信号自身特性出发,评价信号固有抗干扰能力。

(1)模糊图有效面积

定义干扰有效区域面积为对模糊函数进行一定操作后的二维积分,故也称模糊图有效面积:

式中,A(τ,η)为信号单周期模糊函数的模方,即

式中,＊为复数共轭运算,TD为信号周期,τ为时延,η为多普勒频移。

根据模糊函数的体积不变性,并进行归一化得

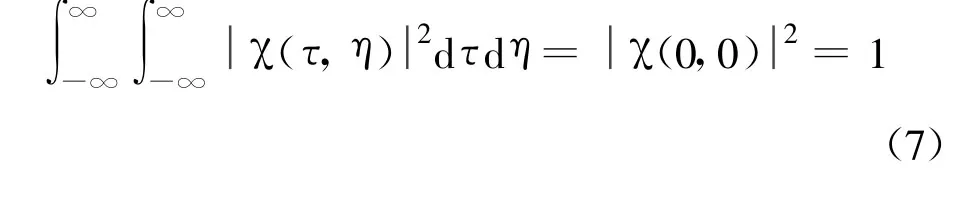
在式(7)的约束下,当模糊函数在有限域内均匀分布时即对于离散情况取值1/NM,模糊图有效面积达最大值(MN)q-1(Δτ Δη)q,其中 N 、M 、Δτ、Δη分别为时延和多普勒的采样点数和采样间隔;而当模糊函数为冲激函数时,有效面积为最小值(Δτ Δη)q;模糊函数在 N1≤N 离散点上均匀分布时的有效面积大于同点数的其他模糊函数的有效面积,且要比在N2≤N1点上均匀分布时的指标值大,两个的比值为(N1/N2)q-1。由此可知,模糊图有效面积确实反映了模糊函数值的集中程度,面积越小,模糊图越尖锐。

信号模糊函数中存在较小的值,可发现当q取大数值时,这些较小的模糊函数值对有效面积的贡献不可忽略,但在计算过程中由于积分域的局限性,往往会忽略掉较小的值而使得有效面积有偏真实。为了提高计算的鲁棒性,q的值不宜取大,取2或4。

(2)模糊图切割面积

模糊图在一定高度下的切割面积为[5]

在一定高度下切割模糊图形成的区域作为有效干扰区域,也符合联合分辨越好或者模糊图越尖锐指标值越低的原则。该度量指标与高度h有关,而高度与信号体制及接收机的信号处理方法和抗干扰措施有关。

3.3 与扩频增益的关系

扩频增益G定义为扩频信号经过相关器前后信噪比的比值。在白噪声环境中,扩频增益为信号带宽Bc与信息带宽Bb之比。经过相关处理,扩频信号在时间上得到压缩并产生相关峰进而提高输出信噪比。从信号模糊函数理论知,信号的时延分辨率δτ与信号带宽近似呈反比关系,于是GBb=Bc≈1/δτ,则扩频增益实际上是对信号在时延维度上的分辨能力的度量。不考虑多普勒维,模糊图有效面积和切割面积的一维表示为

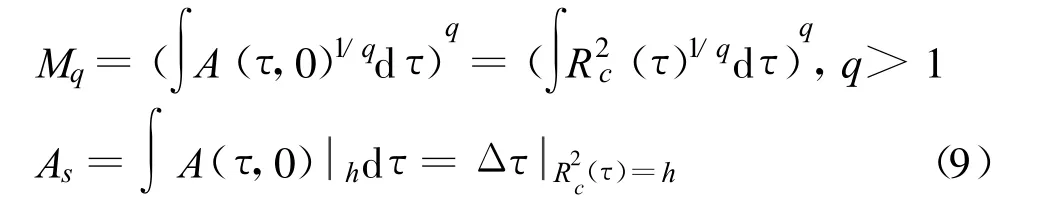
式中,Rc(τ)为时延相关函数。式(9)表明,有效面积和切割面积在时间维度上的表示,也衡量了信号对时延的分辨情况,因此,扩频增益是有效面积和切割面积退化为时间维上的表示,而有效面积和切割面积是扩频增益向时延-多普勒频移的二维扩展形式。

4 仿真与分析

不同码长和码速率下,有效面积和切割面积曲线如图3所示,(a)、(b)中码长为2p-1,p取4～11,码速率1 Mchip/s,(c)、(d)中码率为1～10 Mchip/s。由图3可知,模糊图有效面积及切割面积基本是随着码长增加而减小,即码长越长,信号固有抗干扰性能越好。信号带宽保持恒定,信号在时延维中的分辨宽度不变,但随着码长的增加,在多普勒频移维的分辨宽带减少,有效干扰区域减少。值得注意的是在码长小于63时有效面积取值趋势反向,其原因是模糊图能量太分散而致使数值计算中漏掉很多有用值,故其不适合评价模糊函数值分布偏分散的信号;而当码长较长时,切割面积变化不明显,故其较难区别对比具有良好分辨性能的信号,因此两者对评价信号固有抗干扰性能具有互补特性。从(c)、(d)中可见,有效面积和切割面积几乎不随码速率的变化而变化。信号带宽随码率增加而增加,但信号时长在缩短,其时延-多普勒联合分辨能力不变,信号固有抗干扰性能不变。

图3 有效面积、切割面积与码长、码率的关系Fig.3 Effective and incision areas vs chirp lengths and rates

图4给出了码长为31和255、码速率为1 MHz的直扩信号模糊图及-3 dB切割图,可直观地表现模糊图有效面积及切割面积随码长的变化情况。

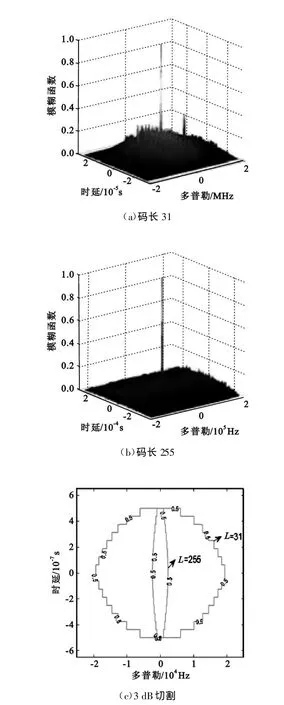
图4 信号模糊图及切割面示意图Fig.4 Ambiguity plots and incision areas

5 结 论

通过对有源干扰的机理分析和扩频测控信号基于相关理论的处理过程的阐述,建立了模糊函数与信号固有抗干扰性能的联系,采用模糊图有效面积及其在一定切割高度下切割面积来度量信号固有抗干扰性能,并指出所提指标实际上是扩频增益向时延-多普勒频移联合域的二维拓展。仿真分析结果表明,模糊图的有效面积和切割面积均可有效反映扩频测控信号固有抗干扰性能,而由于数值计算的近似作用,有效面积不适合评价模糊函数值分布偏分散的信号,而切割面积则较难区分具有良好分辨性能的信号,故两者具有互补特性。该方法既适用于扩频测控信号的评价,也适用于雷达信号、通信信号和引信等。

[1]刘嘉兴,文吉.Ka频段混沌扩频测控系统的设想[J].电讯技术,2009,49(5):33-49.

LIU Jia-xing,WEN Ji.Conception for a Ka-band Chaotic Spread Spectrum TT&C system[J].Telecommunication Engineering,2009,49(5):33-49.(in Chinese)

[2]孟生云,杨文革,王金宝,等.DS/FH测控信号同步方案的捕获性能[J].宇航学报,2010,31(8):2036-2042.

MENG Sheng-yun,Y ANG Wen-ge,W ANG Jin-bao,et al.Acquisition Performance of a Synchronization Scheme of DS/FH Hybrid Spread Spectrum signals for TT&C[J].Journal of Astronautics,2010,31(8):2036-2042.(in Chinese)

[3]Huang Wenzhun,Wang Yongsheng,Ye Xiangyang.Studies on novel anti-jamming technique of unmanned aerial vehicle data link[J].Chinese Journal of Aeronautics,2008,21(2):141-148.

[4]郭琦,高飞,李国民.扩频测控系统抗干扰性能及措施分析[J].飞行器测控学报,2005,24(1):80-84.

GUO Qi,GAO Fei,LI Guo-min.Analysis for performance and measures of anti interference in a spread spectrum TT&C system[J].Journal of Spacecraft TT&C Technology,2005,24(1):80-84.(in Chinese)

[5]赵惠昌,周新刚.基于模糊函数切割法的线性调频连续波引信抗干扰性能测度[J].兵工学报,2009,30(12):1591-1595.

ZHAO Hui-chang,ZHOU Xin-gang.Anti-jamming evaluation of linear frequency-modulated continuous wave fuze based onambiguity function incision[J].Acta Armamentar,2009,30(12):1591-1595.(in Chinese)

[6]Satyabrata Sen,Arye Nehorai.Adaptive Design of OFDM Radar Signalwith Improved Wideband Ambiguity Function[J].IEEE Transactions on Signal Processing,2010,58(2):928-933.

MENG Sheng-yun was born in Maanshan,Anhui Province,in 1983.He is currently working toward the Ph.D.degree.His research interests include TT&C and interference suppression.

Emial:msy-ttc@163.com

杨文革(1966—),男,江西金溪人,教授、博士生导师,主要研究方向为航天器测量与控制、信号处理。

YANG Wen-ge was born in Jinxi,Jiangxi Province,in 1966.He is now a professor and also the Ph.D.supervisor.His research interests include TT&C and signal processing.

Research on Anti-jamming Capability Evaluation Method for Spread Spectrum TT&C Signals

MENG Sheng-yun,YANG Wen-ge
(TT&C Research Center,Equipment Academy,Beijing 101416,China)

Based on the analysis of active jamming mechanism and spread spectrum Tracking Telemetry and Command(SS TT&C)signals processing principle,a method using the ambiguity plots effective areas and the incision areas at a certain level to evaluate inherent anti-jamming capability of SS TT&C signalsis put forward.The smaller the computed areas become,the stronger the anti-jamming performance gets.Simulation results show that the proposed metrics are effective to assess signals anti-jamming performance.The methodology is computable,which provides reference for signals anti-jamming capability evaluation.

TT&C system;spread spectrum signal;inherent anti-jamming capability;ambiguity function

TN974

A

10.3969/j.issn.1001-893x.2012.06.010

1001-893X(2012)06-0883-05

2011-10-31;

2012-04-09

孟生云(1983—),男,安徽马鞍山人,博士研究生,主要研究方向为航天器测量与控制、干扰抑制;