一种基于二阶锥规划的新时差定位算法

金家保,张 颂,杨景曙

(1.解放军电子工程学院信息系,合肥 230037;2.总参陆航研究所,北京 101121)

一种基于二阶锥规划的新时差定位算法

金家保1,张 颂2,杨景曙1

(1.解放军电子工程学院信息系,合肥 230037;2.总参陆航研究所,北京 101121)

针对传统时差定位算法在量测噪声较大情况下定位性能不佳的缺点,提出了一种基于二阶锥规划的新时差定位算法。该算法通过凸松弛和引入惩罚项,将难以求解的用户位置最大似然估计问题转换为一个易于求解的二阶锥规划问题,并将松弛问题的最优解作为用户位置的初始估计,利用传统的泰勒级数展开法得到最终定位结果。仿真给出了不同基站数目及量测噪声下算法的定位性能。仿真结果表明,在量测噪声较大的情况下,新算法的定位精度仍可以逼近理论克拉美罗下限,而且算法中惩罚因子的选取范围易于确定。

到达时差;定位算法;最大似然估计;泰勒级数展开;二阶锥规划;惩罚因子

1 引 言

随着移动通信技术的迅速发展,无线定位技术已经成为第三代移动通信系统所必须具备的业务,而基于用户位置的各种应用也成为最具发展潜力的数据业务之一[1]。移动通信定位根据定位采用的信息不同,可以分为到达信号能量定位法、到达时间(Time of Arrival,TOA)定位法、到达时差(Time Difference of Arrival,TDOA)定位法。由于TDOA定位法不要求移动台与基站之间的时间严格同步,能应用于各种移动通信系统,且定位精度较高,因而受到广泛关注。

在时差定位问题中,由于TDOA量测值与目标位置之间的非线性关系,使得即使在高斯量测噪声的情况下,也难以得到目标位置的最大似然估计。因此,时差定位算法主要集中于求解目标位置的近似最优解,常用的时差定位算法可以分为闭式解法和迭代解法两种。基于泰勒级数(Taylor)展开的迭代算法[2]具有较高的定位精度,但需要一个接近真实位置的初始估计值以避免算法收敛到局部最优解处。闭式解法不需要初始位置估计值,也不存在收敛问题,且计算量较小,但定位精度较差。常见的闭式解法主要有球面插值法(SI)[3]、LCLS方法[4-5]、两步加权最小二乘法(Chan算法[6])等。其中,Chan算法在量测噪声较小的情况下具有较高的定位精度,但随着量测噪声的增大或几何布局不佳时,该算法的定位性能将急剧下降。为了克服Chan算法和Taylor法各自的缺点,文献[7]提出了一种基于Chan算法和Taylor法的组合定位方法,即首先通过Chan算法得到初始用户位置,然后将其作为Taylor法的初始迭代点求解出最终的用户位置。虽然这种组合方法有效地提高了定位精度,但当Chan算法得到的初始用户位置误差较大时,会导致后续迭代无法收敛;另外,当参与定位的基站个数等于3时,Chan算法将求解不出用户初始位置,从而使得这种组合定位算法完全失效。

近年来,随着凸优化理论的发展和成熟,凸优化[8]在信号处理领域的应用也得到了人们的广泛关注,基于凸优化的定位算法也陆续被提出,但这些方法往往是针对TOA定位问题的。本文针对移动用户的TDOA定位问题,提出了一种基于二阶锥规划(Second Order Cone Programming,SOCP)[9]松弛的定位算法,该算法通过凸松弛以及引入惩罚项,将难以求解的非线性非凸最大似然估计问题转换为易于求解的凸优化问题,并将其最优解作为泰勒级数法的初始迭代点从而得到精确的用户位置。计算机仿真实验表明本算法的定位性能优于传统的Chan算法和组合定位法。

2 基本原理

2.1 定位模型

假设定位系统中共有 N个基站,向量 si=[xi,yi]T表示基站i的位置坐标,u=[xu,yu]T表示用户的位置坐标。在假定电磁波传播速度为常数的情况下,基于TDOA与距离差定位是完全一致的。下面的讨论就是建立在距离差上的。不失一般性,以基站s1作为量测参考站,相应的量测方程为

将式(1)写为向量的形式:

定位算法所要解决的问题就是在给定基站位置和一组距离差量测值 d的情况下,如何快速、准确地确定用户的位置。为了充分利用量测信息,本文采用最大似然准则来估计用户位置,假设噪声向量n服从均值为零、协方差阵为Qn的高斯分布,则量测向量 d的似然函数为

其中,K为常数。求使似然函数最大的用户位置坐标值等价于求解如下的优化问题:

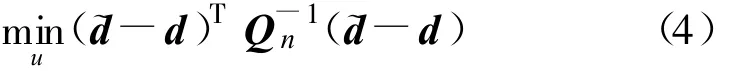
优化问题(4)是一个关于用户坐标的非线性非凸二次优化问题,其全局最优解难以得到,传统的非线性迭代求解方法(如泰勒级数展开法、牛顿法)需要一个接近真实位置坐标的初始估计,否则迭代法难以收敛。

2.2 二阶锥规划简介

所谓SOCP,就是在有限个二阶锥的笛卡尔乘积的仿射子空间的交集上极小化一个线性函数,其数学表述一般为

3 基于二阶锥规划的定位算法

对于难以求解的非线性非凸优化问题(4),首先引入辅助变量ri=‖u-si‖,则问题(4)可以描述为

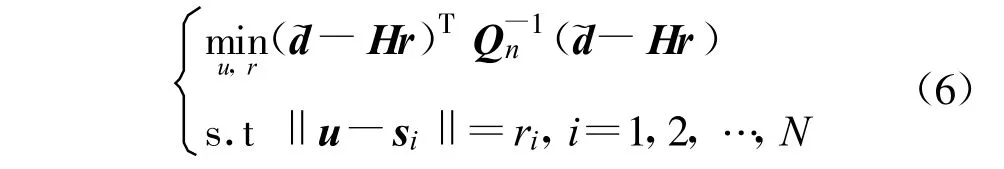
其中,r=[r1,r2,…,rN]T,H=[-1 I],1为(N-1)×N的全1向量,I为单位矩阵。

在优化问题(6)中,目标函数是关于优化变量r的二次凸函数,而非线性的等式约束使的该问题仍然是一个非线性非凸的优化问题。为了将其转化为SOCP问题,考虑将等式约束松弛为不等式约束‖u-si‖≤ri,并引入惩罚项 ρ rTr对松弛的约束条件加以限制,则可以得到松弛后的优化问题为

其中,ρ>0是一个较小的常数,称为惩罚因子。

为了将优化问题(7)表示成SOCP形式,首先对目标函数进行如下变换:

将式(8)代入问题(7)中,注意到目标函数中的常数项并不影响优化问题的求解,将其忽略得到

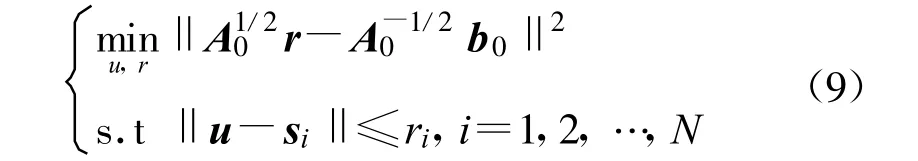
再次引入辅助变量ξ,则优化问题(9)与下述优化问题等价:

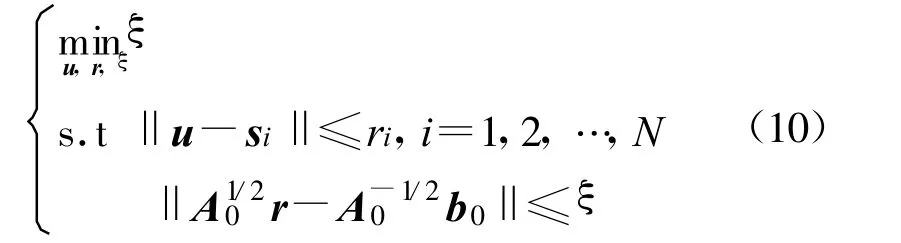
至此,得到一个与问题(7)完全等价的SOCP问题(10),其全局最优解可以通过内点算法[9]进行有效求解,具体求解过程此处不再叙述。得到其全局最优解 x＊=(u＊,r＊,ξ＊),x＊中的 u＊即为用户位置估计,将其作为Taylor级数展开法的初始位置估计,进一步提高用户位置估计精度。

4 仿真实验

为了评估和比较算法的定位性能,并考虑实际中可能出现的多种情况,进行了2 000次统计独立的Monte-Carlo仿真实验。量测噪声 n为零均值高斯分布,其协方差矩阵Qn主对角线上的元素值为σ2d,非主对角线元素的值为0.5σ2d,即假设各基站之间的量测噪声是相互独立的,采用定位结果的均方根误差(Root Mean Square Error,RMSE)来衡量算法的定位性能,实验中通过逐次改变噪声方差的值,得到不同噪声方差下算法的定位性能。N表示参与定位的基站数目,SOCP问题采用凸优化工具箱CVX进行求解。

(1)实验1(N=3)

本实验中,用户位置为u=(40 m,30 m)T,3个基站的坐标分别为 s1=(-20 m 80 m)T,s2=(120 m 40 m)T,s3=(0 m-60 m)T。图1给出了SOCP松弛算法(惩罚因子设为ρ=10-6)和Chan算法在不同量测噪声方差下的定位误差RMSE曲线,同时为了评估算法的性能,给出了定位RMSE的克拉美罗下限(Cramer-Rao Lower Bound,CRLB)。由于Chan算法中的系数矩阵在N=3时为奇异阵,本实验中用伪逆操作代替了原始的求逆操作。从实验结果中看以看出,在基站数目为3时,本算法不但能够完成对用户的位置估计,并且定位性能达到了CRLB,而Chan算法在这种情况下则无法完成用户的有效定位。

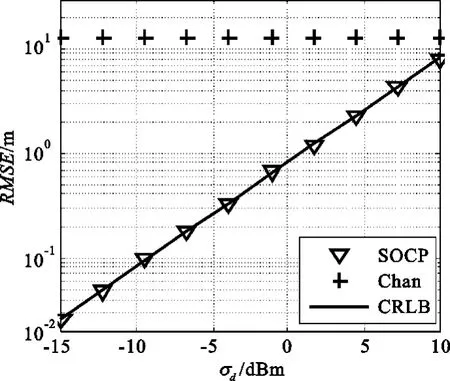
图1 不同量测噪声下的定位RMSEFig.1 Location R MSE versus measurement noise

惩罚因子对SOCP松弛定位算法的性能有着很大影响,为了确定惩罚因子合适的选取范围,分别就两种不同量测噪声情况下,惩罚因子对定位性能的影响进行了研究,结果如图2所示。从中可以看出,惩罚因子的合适选取范围为[10-7,10-2],在此区间内该算法均可完成对用户的有效定位。

图2 惩罚因子对定位R MSE的影响Fig.2 Location R MSE versus different penalty factor

(2)实验2(N>3)

本实验考虑超定情况下算法的定位性能,设定4个基站,各基站坐标为 s1=(80 m 98 m)T,s2=(70 m-80 m)T,s3=(-80 m-75 m)T,s4=(-91 m 82 m)T。用户位置为 u=(12 m,10 m)T。分别就SOCP松弛算法、Chan算法、Chan+Taylor组合法、SOCP+Taylor组合算法的定位性能进行了研究,其中SOCP松弛算法中的惩罚因子仍设为10-6,仿真结果如图3所示。在量测噪声较小的情况下,Chan算法、Chan+Tayor组合法以及SOCP+Taylor组合法的定位精度相当,都可以达到定位的CRLB。但随着量测噪声的增大,Chan算法的性能开始急剧下降,基于该算法的组合定位法由于初始用户位置估计误差较大,定位误差RMSE迅速增大,并且会出现无法收敛的情况。SOCP松弛算法的定位性能却始终比较稳定,并且基于该方法的组合定位算法在量测噪声较大时仍可以达到定位的CRLB。

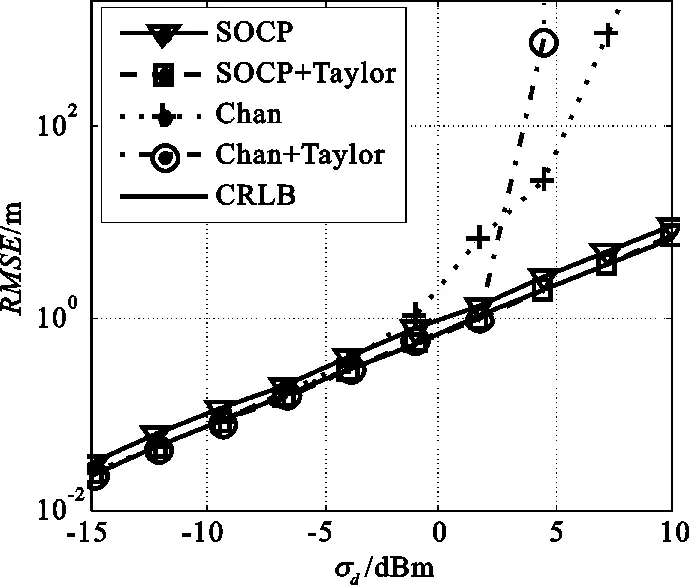
图3 不同量测噪声下的定位R MSEFig.3 Location RMSE versus measurement noise

图4给出了本实验场景下惩罚因子对SOCP松弛算法的影响。从结果中可以看出,使算法有效的合适区间为[10-7,10-2],与实验1中的相同。可见不同场景以及不同的量测噪声对惩罚因子的选取范围基本没有影响。

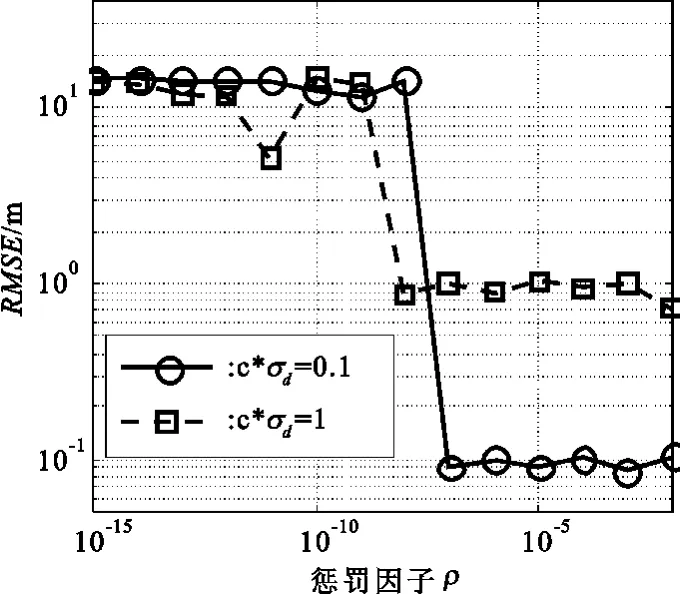
图4 惩罚因子对定位RMSE的影响Fig.4 Location RMSE versus different penalty factor

5 结束语

针对基于时差量测信息的移动用户定位问题,本文提出了一种基于SOCP的时差定位方法。仿真结果表明,基于SOCP松弛的新时差定位算法对量测噪声不敏感,具有较好的定位性能。在基站数目为3时,相比于其他定位算法,文中所提算法仍可以实现用户的有效定位;当基站数目大于3时,通过将本算法的位置估计作为Taylor展开法迭代的初始点,可以取得逼近于CRLB的定位性能。本算法求解一次用户位置的时间大约为1 ms,且算法中的惩罚因子选取范围容易确定,在工程上具有一定的应用前景。

[1]Zekavat R,Buehrer R M.Handbook of Position Location:Theory,Practice and Advances[M].Wiley:IEEE,2010:25-28.

[2]Foy W H.Position-Location Solutions by Taylor-series Estimation[J].IEEE Transactions on Aerospace and Electronic Systems,1976,12(2):187-193.

[3]Schau H C,Robinson A Z.Passive Source Localization employing intersecting spherical surfaces from time-of-arrival differences[J].IEEE Transactions on Acoustics,Speech,and Signal Processing,1987,35(8):1223-1225.

[4]Yiteng Huang,Jacob Benesty,Elko G W,et al.Real-time Passive Source Localization:A Practical Linear-Correction Least-Squares Approach[J].IEEE Transactions on Speech and Audio Processing,2001,19(8):943-956.

[5]Beck A,Stoica P,Li Jian.Exact and Approximate Solutions of Source Localization Problems[J].IEEE Transactions on Signal Processing,2008,56(5):1770-1778.

[6]ChanY T,Ho K C.A Simple andEfficient Estimator for Hyperbolic Location[J],IEEE Transactions on Signal Processing,1994,42(8):1905-1915.

[7]熊瑾煜,王巍,朱中梁.基于泰勒级数展开的蜂窝TDOA定位算法[J].通信学报,2004,25(4):145-150.XIONG Jin-yu,W ANG Wei,ZHU Zhong-liang.TDOA location algorithm based on T aylor series expansion[J].Journal on Communications,2004,25(4):145-150.(in Chinese)

[8]Boyd S,Vandenberghe L.Convex Optimization[M].Cambridge,UK:Cambridge University Press,2005.

[9]Lobo M S,Vandenberghe L,Boyd S,et al.Applications of second-order cone programming[J].Linear Algebra and its Application,1998,284(1-3):193-228.

JIN Jia-bao was born in Changfeng,Anhui Province,in 1982.He received the M.S.degree in2008.He is currently working toward the Ph.D.degree.His research concerns passive location and convex optimization application.

Email:jin-jiabao@qq.com

张 颂(1984—),男,江苏徐州人,2011年获博士学位,现为工程师,主要研究方向为无线电通信、信号处理等;

ZHANG Song wasborn in Xuzhou,Jiangsu Province,in1984.He received the Ph.D.degree in 2011.He is now an engineer.His research interestsinclude wireless communication and signal processing.

杨景曙(1950—),男,安徽合肥人,教授、博士生导师,主要研究方向为无源定位、通信信号处理、导航技术等。

YANG Jing-shu was born in Hefei,Anhui Province,in 1950.He is now a professor and also the Ph.D.supervisor.His research concerns passive location,signal processing and radio navigation.

A New TDOA Location Algorithm Based on Second Order Cone Programming

JIN Jia-bao1,ZHANG Song2,YANGJing-shu1
(1.Information Department,Electronic Engineering Institute,Hefei 230037,China;2.The Army Aviation Research Institute of Headquarters of General Staff,Beijing 101121,China)

The traditional TDOA(Time Difference of Arrival)location algorithms have large performance loss as the measurement noise is high.To overcome this drawback,this paper proposes a new effective TDOA location algorithm based on second order cone programming(SOCP).By introducing a penalty term and relaxing the equality constrains,the nonlinear and nonconvex maximum likelihood estimation problem for user position is transformed into a convex optimization problem,named second order cone programming that can be efficiently solved by modern interior point methods.The optimal solution of relaxed problem is used as the initial guess for traditional Taylor method to estimate the user position.The simulation provides the location performance versus measurement noise under different numbers of base station.Simulation results show that the performance of proposed algorithm can attain the Cramer-Rao lower bound as the noise variance is high.The intervals of penalty factor are also discussed in this paper.

TDOA;location algorithm;maximum likelihood estimator;Taylor series expansion;second order cone programming;penalty factor

TN929.5

A

10.3969/j.issn.1001-893x.2012.06.011

1001-893X(2012)06-0888-05

2012-04-11;

2012-06-04

金家保(1982—),男,安徽长丰人,2008年获硕士学位,现为博士研究生,主要研究方向为无源定位、凸优化应用等;