线性调频-伪码调相复合信号的伪码盲估计新算法

何丹娜,张天骐,高春霞,高 丽

(重庆邮电大学信号与信息处理重庆市重点实验室,重庆 400065)

线性调频-伪码调相复合信号的伪码盲估计新算法

何丹娜,张天骐,高春霞,高 丽

(重庆邮电大学信号与信息处理重庆市重点实验室,重庆 400065)

针对线性调频-伪码调相复合信号的伪码估计问题,提出一种基于离散多项式相位变换和频谱搬移的伪码盲估计新算法。首先采用平方法消去伪码的相位突变,然后利用离散多项式相位变换估计调频斜率,利用估计的高精度调频斜率重构二阶指数项,对原复合信号进行解线调,再对解线调后的信号取实部从而可得正弦载波与伪码调相的复合信号,采用频谱搬移的方法可恢复出原伪码序列。仿真结果表明,该算法在信噪比大于等于3 dB时可正确估计出伪码,且性能随子脉冲个数的增加而改善,与FM-AM时频分析方法相比具有更好的估计效果。

线性调频-伪码调相;离散多项式相位变换;频谱搬移;伪码盲估计

1 引 言

线性调频-伪码调相复合信号(LFM-PRBC)是一种脉内调频、脉间调相的复合信号,既具有伪码调相信号良好的抗干扰能力,又具有线性调频信号对多普勒频移的不敏感性,因而具有截获概率低、抗干扰性能好等优点。目前,这种复合信号已被用于多种雷达和微小型探测器中,所以研究该信号的参数估计和伪码估计具有重要意义。

目前,针对该复合信号已提出各种参数估计方法。文献[1-2]提出基于循环谱的时差估计方法,但需已知码片宽度和载频。文献[3-4]采用谱相关的方法进行参数估计和信号识别,需满足调频带宽大于伪码数与脉冲宽度之比,且计算量大、运行时间长。文献[5-6]提出了基于时频分布函数的参数估计算法,由于要进行时频平面的二维搜索,该算法计算量大且较复杂。文献[7-8]提出了快速参数估计算法,该算法计算量小且实时性好。以上文献只是针对线性调频-伪码调相复合信号的参数进行估计,并没有涉及伪码的估计。文献[9]中提出频谱搬移的方法用来实现正弦波调制的伪码调相信号的伪码估计,该方法要进行两次快速博里叶变换(FFT),计算量较大。文献[10]中采用基于FM-AM时频分析方法可对该复合信号的码型进行估计,但涉及滤波器组的设计及多次乘法运算,实现较为复杂。目前,针对线性调频-伪码调相复合信号的伪码盲估计的研究很少,本文将深入研究这个难点问题。

本文的核心思想是先消除伪码的相位突变,再利用多项式相位变换估计调频斜率用以解线调,从而将线性调频信号降阶为单音频信号,然后利用频谱搬移的方法恢复出伪码序列。

2 信号模型

线性调频-伪码调相复合信号的时域表达式为[11]

本文只考虑一个伪码周期内的信号(即N=1),此时该复合信号可表示为

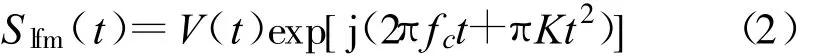
3 伪码盲估计的算法原理

3.1 线性调频-伪码调相复合信号的解线调

假设已经估计出伪码调相信号的子脉冲宽度Tp、子脉冲重复周期T1、子脉冲个数P这几个参数,而线性调频信号的载频和调频斜率未知。设接收到的信号为

式中,s(t)为接收到的线性调频-伪码调相复合信号,w(t)是均值为0、方差为的高斯白噪声。

对接收的信号以Ts为采样间隔进行采样,采样后的接收信号为

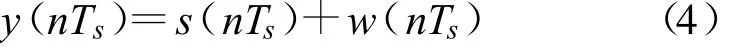
为了简化,令 n=nTs,则上式表示为

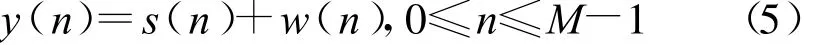
式中,s(n)为采样后的线性调频-伪码调相复合信号,w(n)是采样后的高斯白噪声序列,M为采样后信号的长度。对该复合信号进行伪码的估计,首先要通过解线调的方法消除信号的线性调制,使其变成单频率载波与伪码调相的复合信号。解线调的结构框图如图1所示。

图1 线性调频-伪码调相复合信号的解线调结构框图Fig.1 Block diagram of dechirp of LFM-PRBC signal

首先利用平方法对采样后的信号进行处理,使伪码的符号由随机的±1变为1,消除了伪码的相位突变。将式(5)平方后为

其中:

式中,slfm1(n)为经平方后新的线性调频信号,载频为2fc,调频斜率为2K;w1(n)是经平方后产生的新的噪声。

线性调频信号是多项式相位信号的一种特殊形式,它的最高阶数为2,则可以采用离散多项式相位变换的方法[12]来估计线性调频的参数。由于该方法在估计最高阶系数时比较精确,而其他系数的估计依赖于最高阶系数估计的精度,存在传递误差,所以这里只用该方法估计调频斜率。

令z(n)=y2(n)为平方后的信号,则z(n)的二阶瞬态矩表示为

式中,R为有用信号与噪声、噪声和噪声的延迟相乘之和,可看作对有用信号二阶瞬态矩的噪声干扰。

经DP2[z(n),τ]变换将接收信号变为正弦信号和新的噪声,通过FFT将在 ω0处呈现峰值,从而可从最大峰值估计出调频斜率:

式中 ,ω0=2!τ a2,由于最高阶系数 a2=2πK,则调频斜率的估计值 K= a2/2π。

通过上式得到了调频斜率K的精确估计,故可重构二阶指数项exp[j(π Kn2)],将重构二阶指数项的共轭与接收到的信号相乘,有

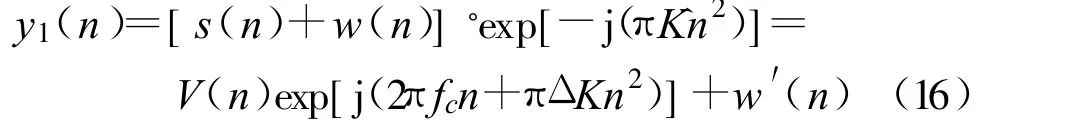
式中,Δ K=K- K为调频斜率的真实值与估计值的差值,w′(n)为噪声与二阶指数项相乘后新的噪声,当 Δ K 较小时就有 exp(jπΔ Kn2)≈1,此时

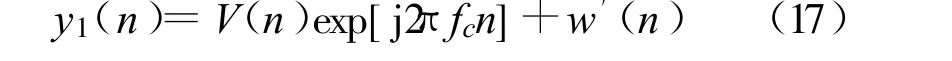
由式(17)得到的y1(n)是解线调后的单音频信号与伪码调相的复合信号及产生的新噪声,接下来对该信号进行伪码估计。

3.2 伪码的盲估计

对上一节得到的信号y1(n)取实部得

式中,real(·)表示取信号的实部。从式(18)可以看出,此时y2(n)的有用信号为正弦波与伪码调相的复合信号,正弦载波的作用相当于对伪码调相信号进行了上变频处理,通常为了得到基带伪码调相信号采用下变频的方法。

将式(19)通过低通滤波器滤除高频分量,便可得基带伪码信号V(n),从而可以恢复出伪码序列。

但实际对载频fc的估计不可能做到完全准确,此时估计值与真实值之间存在偏差(即频偏),在频偏存在的情况下,利用下变频的方法获得伪码调相信号时会出现误差。

令估计的载频f′c=fc+Δfc,Δfc即为频偏,此时式(19)变为

上式通过低通滤波器滤除高频分量后,还是有残留频偏引起的正弦波存在,这使得伪码序列不能正确地恢复出来,因此通过下变频恢复伪码序列的时域方法是不可行的。

通过分析上述时域方法有很大的局限性,因此考虑在频域进行伪码序列的恢复。

信号y2(n)的傅里叶变换为

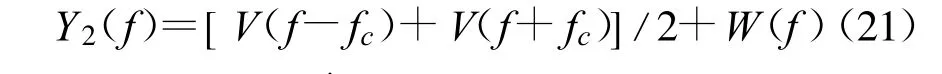
其中,W(f)为real(w′(n))的傅里叶变换,[V(f-fc)+V(f+fc)]/2为正弦波与伪码调相复合信号的频谱,且有

由式(22)可以看出,伪码调相信号的频谱包络近似为sa(πfTp),主瓣宽度窄且高,旁瓣相比较占的频谱很宽且幅度低。正弦载波的作用相当于将伪码信号的频谱分别向两边频移了 fc,形状没有发生变化。当fc较小时V(f-fc)和 V(f+fc)混叠的部分较多,当fc较大时V(f-fc)和 V(f+fc)混叠的部分较少。频谱搬移的思想是:先对接收的信号进行FFT变换,对变换后的频谱进行搬移,使之恢复伪码序列的频谱,再进行IFFT变换,从而得到所求的伪码序列。该算法流程如下:

(1)对信号y2(n)进行长度为2M的FFT变换(M为信号y2(n)的长度),记为Y2(f),此时频谱关于中心位置是对称的;

(2)将频谱沿中心位置对折相加,相加后的频谱记为Y21(f),此时Y21(f)频谱的长度为Y2(f)的一半,即为 M;

(4)对频谱进行搬移,得所求伪码信号的频谱为 V(f)=[Y21(α:M),Y21(1:α-1)];

(5)对搬移后的频谱 V(f)进行IFFT变换,取前半个周期序列可得正确的伪码序列。

该算法的实质是通过FFT变换及频谱的搬移,将频偏抑制从而不会对伪码估计产生影响,且不存在反码的问题。只是由于第一步中进行的傅里叶变换的长度是信号长度的2倍,使得恢复出来正确的伪码序列的长度是原序列长度的一半,由于伪码的参数是已知的,可对估计出来的伪码序列扩展得原长度的序列波形。单音频信号与伪码调相复合信号的伪码估计原理见图2。图2中累加平均的作用是使伪码序列保持不变而大部分噪声被平均掉,从而使恢复出来的序列波形清晰可见。

图2 单音频信号与伪码调相复合信号的伪码估计结构框图Fig.2 Block diagram of the PN code estimation of reconnaissance signal combined single tone signal and PRBC

3.3 计算复杂度分析

针对本文提出的伪码盲估计算法,以复数乘法作为衡量计算复杂度的指标。设经采样后接收信号的长度为M,则经平方法去除伪码相位突变需要M次复数乘法,离散多项式相位变换主要包括延时相乘和FFT变换,延时相乘需要约0.5M次复数乘法,FFT变换需要50Mlb(100M)次复数乘法,重构二阶指数项的共轭与接收信号相乘所需M次复数乘法,伪码估计时FFT变换需要Mlb(2M)次复数乘法,IFFT变换需要(Mlb(M))/2次复数乘法,则总计需要的复数乘法约为3.5M+Mlb(2M)+(Mlb(M))/2+50Mlb(100M)。

4 仿真实验及其分析

实验一:设接收的信号为

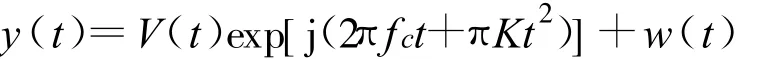
式中,w(t)为高斯白噪声。其中,子脉冲宽度 Tp=0.3 μ s,子脉冲重复周期 T1=0.5 μ s,子脉冲个数 P=7,载频 fc=100MHz,调频斜率K=30×1012Hz/s,采样频率为fs=128MHz。

图3给出了线性调频-伪码调相复合信号平方后分别在没有噪声和信噪比为10 dB时经过瞬态矩变换后的信号实部幅值特性图。从图中可以看出,在没有噪声时,经过瞬态矩后,信号变为带有占空比的正弦波,信号二阶瞬态矩的长度与延时有关,若延时越大,则信号二阶瞬态矩的长度越小,反之,则信号二阶瞬态矩的长度越长。对于线性调频信号而言,延时 τ一般取采样后信号长度的一半。当信噪比为10 dB时信号为正弦波和新的噪声。图4给出信噪比为10 dB时信号的二阶瞬态矩经离散多项式相位变换后的谱线,从最大峰对应的位置可以得到调频斜率。

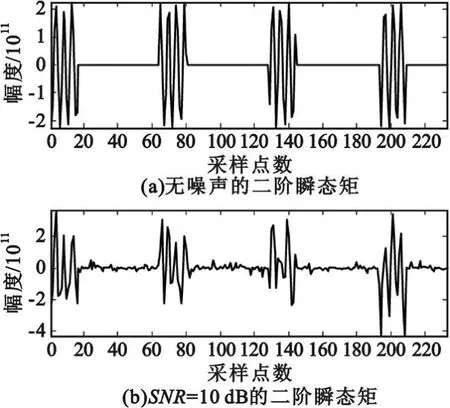
图3 平方后LFM-PRBC信号的二阶瞬态矩Fig.3 Transient second-order moment of squared LFM-PRBC signal

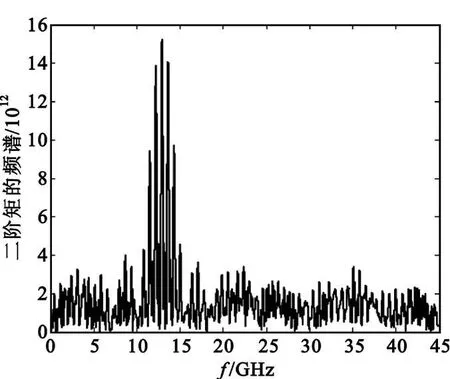
图4 多项式相位变换谱线图Fig.4 Spectral line graph of polynomial phase transform

图5是经过200次Monte-Carlo仿真的结果,它给出了调频斜率的均方误差和CRB随信噪比变化的曲线,从图中可以看出信噪比小于10 dB时,随着信噪比的增大,线性调频的均方误差与CRB越来越接近,此时理论值与真实值的偏差逐渐减小;当信噪比大于等于10 dB时,随着信噪比的增加,调频斜率的均方误差保持不变。

图5 LFM-PRBC信号的调频斜率估计Fig.5 Chirp rate estimation of LFM-PRBC

实验二:在实验一的基础上,对正弦波与伪码调相复合信号的伪码进行估计,参数和实验一相同,并仿真子脉冲个数不同时的正确估计次数性能曲线。

图6给出了信噪比为5 dB时正弦波与伪码复合信号的频谱,从图中可以清楚地看到两个较高的主瓣,旁瓣范围较宽且易受到噪声的影响,两个主瓣之间的部分旁瓣是混叠的,这是由于频移而产生的。图7给出了信噪比为5 dB时,经过累加平均后恢复出来的伪码序列波形,从图中可以看出恢复出来的伪码序列与原序列相比,符号完全相同,只是长度减为原序列的一半。通过下采样及取符号可得伪随机二进序列 -1,1,-1,1,-1,-1,-1。

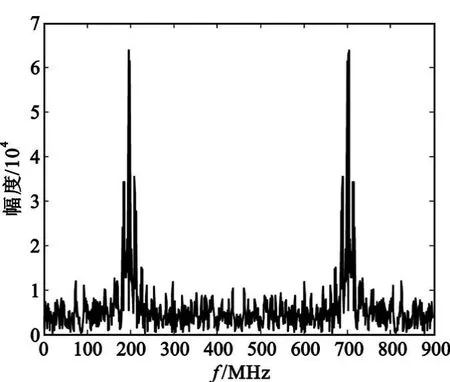
图6 正弦波与伪码复合信号的频谱Fig.6 Spectrum of reconnaissance signal combined sine wave and PRBC

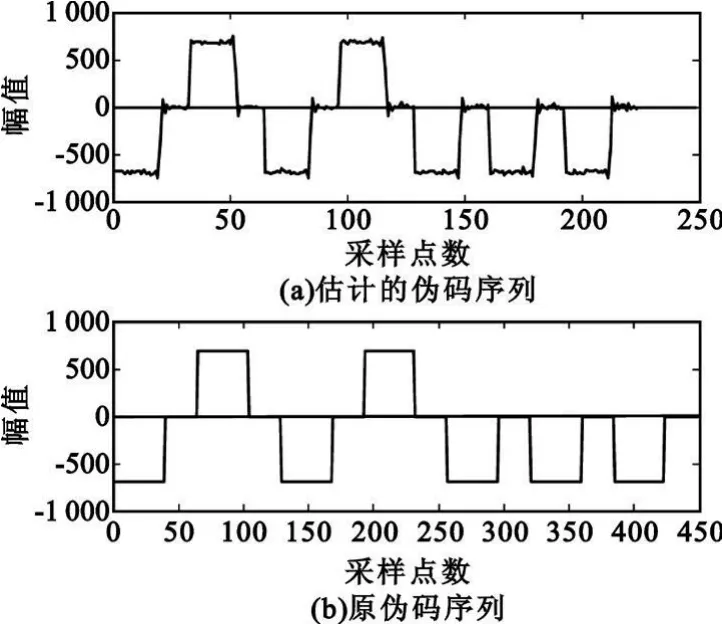
图7 估计的伪码序列Fig.7 Estimated PN sequence

图8是进行200次实验用来验证不同子脉冲条件下正确估计的性能。从图中可以看出随着信噪比的增大,正确估计的次数逐渐增大,到25 dB时都趋近200次。在同一信噪比下,子脉冲个数越多,正确估计次数越大。从图中还可以清楚地看到子脉冲个数多的可以工作在更低的信噪比下,估计性能更好,当子脉冲个数为31时,在信噪比为0 dB时也可以正确估计出伪码序列,且当信噪比大于等于5 dB时,正确估计率达到90%以上。

图8 不同子脉冲个数的性能分析Fig.8 Performance analysis for numbers of sub-pulse

图9给出了子脉冲个数为7时,本文算法与文献[10]中提出的FM-AM时频分析方法的性能对比。从图中可见,同一信噪比下,本文算法的正确检测概率高于FM-AM时频分析方法,由此表明本文算法具有一定的优越性。

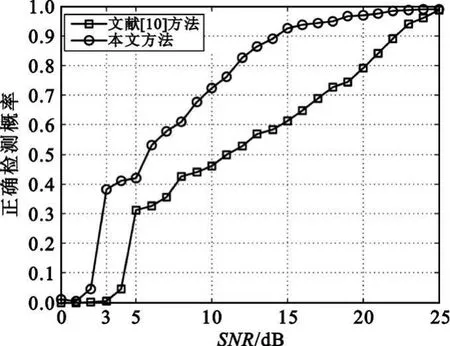
图9 性能对比曲线Fig.9 Performance comparison

5 结 论

本文提出一种基于离散多项式相位变换和频谱搬移的线性调频-伪码调相复合信号的伪码盲估计算法。首先采用平方法消去伪码的相位突变,然后采用离散多项式相位变换估计调频斜率,通过估计的调频斜率重构二阶指数项用来对该复合信号解线调,再对解线调后的信号取实部从而可得正弦载波与伪码调相的复合信号,通过频谱搬移的方法可恢复出原伪码序列。通过相应的仿真分析可以看出该方法有效、可行。与FM-AM时频分析方法相比,本文算法在子脉冲个数为7时可在信噪比大于等于3 dB的情况下正确估计伪码,随着子脉冲个数的增大,估计性能进一步提高,在子脉冲个数为31时可达到信噪比为0 dB,且本文的算法不涉及滤波器组的设计,实现较为简单。因此本文的算法将为解决该类伪码体制复合信号的伪码盲估计提供一种途径,为电子侦察和抗干扰通信的研究铺平道路。

由于本文提出的伪码盲估计算法中间步骤较多,存在误差传播,且伪码估计性能的好坏受到调频斜率估计的影响,后期工作将围绕这方面深入研究,以便进一步提高伪码的估计性能。

[1]Gardner W A,Spooner CM.Detection and source location of weak cyclostationary signals:simplifications of the maximum-likelihood receiver[J].IEEE Transactions on Communications,1993,41(6):905-916.

[2]Chin-Kang C,Gardner W A.Signal-selective time-difference-of-arrival estimation for passive location of manmade signal sources in highly corruptive environments:Theory and method[J].IEEE Transactions on Signal Processing,1992,40(5):1168-1184.

[3]熊刚,赵惠昌,林俊.伪码-载波调频侦察信号识别的谱相关方法(I):伪码-载波调频信号的谱相关函数[J].电子与信息学报,2005,27(7):1081-1086.

XIONG Gang,ZHAO Hui-chang,LIN Jun.Reconnaissance signal recognition of PN code-carrier FM based on spectral correlation method(I):spectral correlation function of PN code-carrier FM[J].Journal of Electronics&Information Technology,2005,27(7):1081-1086.(in Chinese)

[4]熊刚,赵惠昌,王李军.伪码-载波调频侦察信号识别的谱相关方法(II):伪码-载波调频信号的调制识别和参数估计[J].电子与信息学报,2005,27(7):1087-1092.

XIONG Gang,ZHAO Hui-chang,WANG Li-jun.Reconnaissance signal recognition of PN code-carrier FM based on spectral correlation method(II):The modulation recognition and parameter estimation of PN code-carrier FM[J].Journal of Electronics&Information Technology,2005,27(7):1087-1092.(in Chinese)

[5]林俊,熊刚,王智学.基于时频分析的伪码与线性调频复合体制侦察信号参数估计研究[J].电子与信息学报,2006,28(6):1045-1048.

LIN Jun,XIONG Gang,WANG Zhi-xue.Study on reconnaissance signal parameter evaluation of PN and LFM based on time-frequency analysis[J].Journal of Electronics&Information T echnology,2006,28(6):1045-1048.(in Chinese)

[6]熊刚,杨小牛,赵惠昌.基于平滑伪Wigner分布的伪码与线性调频复合侦察信号参数估计[J].电子与信息学报,2008,30(9):2115-2119.

XIONG Gang,YANG Xiao-niu,ZHAO Hui-chang.Parameter estimation of reconnaissance signal combined PN and LFM based on smoothed pseudo Wigner distribution[J].Journal of Electronics&Information Technology,2008,30(9):2115-2119.(in Chinese)

[7]曾德国,熊晖,龙柯宇,等.伪码-线性调频复合信号快速参数估计方法[J].系统工程与电子技术,2010,32(5):891-894.

ZENG De-guo,XIONG Hui,LONG Ke-yu,et al.Fast parameter estimation approach of reconnaissance signal combined PRBC and LFM[J].Systems Engineering and Electronics,2010,32(5):891-894.(in Chinese)

[8]张佳芬,和小冬,唐斌.伪码-线性调频信号快速参数估计算法[J].电讯技术,2009,49(12):100-104.

ZHANG Jia-fen,HE Xiao-dong,TANG Bin.A Fast parameter estimation approachfor multiplicative signal combined PRBC and LFM[J].Telecommunication Engineering,2009,49(12):100-104.(in Chinese)

[9]熊波,秦钊,路明,等.伪码调相脉冲信号识别[J].四川兵工学报,2011,32(9):73-74.

XIONG Bo,QIN Zhao,LU Ming,et al.PN code phase modulation pulse signal recognition[J].Journal of Sichuan Ordnance,2011,32(9):73-74.(in Chinese)

[10]李明孜,赵惠昌.伪码体制复合引信信号识别及参数提取技术研究[D].南京:南京理工大学,2006.

LI Ming-zi,ZHAO Hui-chang.Study on signal recognition and parameter extraction of pseudo-code compound system fuze[D].Nanjing:Nanjing University of Science and Technology,2006.(in Chinese)

[11]朱晓华.脉位调制脉冲串雷达信号理论与应用研究[D].南京:南京理工大学,2002.

ZHU Xiao-hua.Study on pulse-position-modulated pulse-sequence radar signal theory and its applications[D].Nanjing:Nanjing University of Science and Technology,2002.(in Chinese)

[12]高春霞,张天骐,金翔,等.基于离散多项式变换的宽带线性调频信号波达方向估计[J].计算机应用,2011,31(10):2872-2875.

GAO Chun-xia,ZHANG Tian-qi,JIN Xiang,et al.Arrival direction estimationof wideband linear frequency modulation signal based on DPT[J].Journal of Computer Applications,2011,31(10):2872-2875.(in Chinese)

HE Dan-na was born inTianshui,Gansu Province,in 1988.She received the B.S.degree from Chongqing University of Posts and Telecommunications in 2010.She is now a graduate student.Her research direction is blind detection and estimation of composite signal in high dynamic system.

Email:hedanna886@163.com

张天骐(1971—),男,四川眉山人,现为教授、硕士生导师,主要从事宽带微弱无线电信号处理、盲信号与信息处理以及通信对抗理论研究;

ZHANG Tian-qiwas born in Meishan,Sichuan Province,in 1971.He is now a professor and also the instructor of graduate students.His research interests include weak wideband radio signal processing,blind signal and information processing,communication confrontation theory.

Email:zhangtq@cqupt.edu.cn

高春霞(1987—),女,河南周口人,硕士研究生,主要研究方向为宽带信号的波达方向估计、阵列信号处理;

GAO Chun-xia was born in Zhoukou,Henan Province,in 1987.She is now a graduate student.Her research interests include DOA estimation of broadband signal and array signal processing.

Email:gaochunxia888@163.com

高 丽(1985—),女,山东菏泽人,2010年于菏泽学院获学士学位,现为硕士研究生,主要研究方向为图像和通信信号的盲源分离。

GAO Li was born in Heze,Shandong Province,in 1985.She received the B.S.degree from Heze University in 2010.She is now a graduate student.Her research direction is blind source separation of image and communications signals.

Email:gaoli5106794@126.com

The NationalNaturalScience Foundation of China(No.61071196,61102131);The Program for New Century Excellent Talents in University(NCET-10-0927);The Project of Key Laboratory of Signal and Information Processing of Chongqing(CSTC2009CA2003);The Chongqing Distinguished Youth Foundation(CSTC2011jjjq40002);The Natural Science Foundation of Chongqing(CSTC2009BB2287,CSTC2010BB2398,CSTC2010BB2409,CSTC2010BB2411)

A New Blind Estimation Algorithm for PN Code of Reconnaissance Signal Combined PRBC and LFM

HE Dan-na,ZHANG Tian-qi,GAO Chun-xia,GAO Li
(Chongqing Key Laboratory of Signal and Information Processing,Chongqing University of Posts and Telecommunications,Chongqing 400065,China)

A new algorithm is proposed to blindly estimate the pseudo noise(PN)code of reconnaissance signal combined pseudo-random binary phase code(PRBC)and linear frequency modulated(LFM),which uses methods of discrete polynomial-phase transform(DPT)and spectrum shifting.Firstly,the square of the

signal is computed to eliminate the phase mutation.Then,DPT is adopted to obtain chirp rate,which is used to reconstruct the second-order index.The original signal is multiplied by the conjugated second-order index to get a new compound signal.And then,the real part of the new compound signal is made of a sine carrier and the PRBC signal,the original pseudo-code sequence can be restored by the way of spectrum shifting.Simulation results show that the algorithm can correctly estimate PN code when the signal-to-noise ratio(SNR)is greater than or equal to 3 dB,and performance will be improvedwith the increase in the number of sub-pulse.It also has a better performance compared with FM-AM time-frequency analysis method.

LFM-PRBC;discrete polynomial-phase transform;spectrum shifting;blind estimation of PN code

TN911.7

A

10.3969/j.issn.1001-893x.2012.06.015

1001-893X(2012)06-0906-07

2012-01-20;

2012-03-16

国家自然科学基金资助项目(61071196,61102131);教育部新世纪优秀人才支持计划项目(NCET-10-0927);信号与信息处理重庆市市级重点实验室建设项目(CSTC2009CA2003);重庆市杰出青年基金项目(CSTC2011jjjq40002);重庆市自然科学基金资助项目(CSTC2009BB2287,CSTC2010BB2398,CSTC2010BB2409,CSTC2010BB2411)

何丹娜(1988—),女,甘肃天水人,2010年于重庆邮电大学通信与信息工程学院获学士学位,现为硕士研究生,主要研究方向为高动态体制复合信号的盲检测与盲估计;