WSN中一种基于延迟限定的数据收集算法

赵 通

(武汉理工大学信息工程学院，湖北武汉430070)

0 引言

综合了无线通信技术、传感器技术、嵌入式计算技术和分布式信息处理技术的无线传感器网络(Wireless Sensor Network，WSN)是目前国际上前沿热点的研究领域。传感器节点能够协作地实时监测、感知网络区域内各种信息，然后以多跳的方式将这些信息传送给远方的基站(Sink)［1］。在一些持续性的监视应用中，如:森林火警监视、矿道瓦斯监测和战场监控等，不仅要求网络能保存能量长期地工作，还要求网络在收集到数据后能尽快地将数据传送给用户进行处理，即网络需要满足最大化生命周期和最小延迟这2个要求。下面针对该问题进行研究。

1 相关工作

目前有很多工作分别研究网络生命周期最大以及传输延迟最小的数据收集协议，以达到目标的方式进行划分，主要有以下3类:① 功率控制。就是为传感器节点选择合适的发射功率。比较典型的协议有:拓扑控制维护网络连接(TCMNC)［2］和能量与延迟协议(TOED)［3］等。②睡眠调度。就是控制传感器节点在工作状态和睡眠状态之间的转换。比较典型协议有:延迟敏感的寿命最大化(MLDS)［4］和最小能量消耗(MEC)［5］。睡眠调度能使冗余节点进入睡眠状态，大幅度地降低网络的能量消耗和竞争信道冲突，这对于节点密集型和事件驱动型的网络十分有效。但它需要在保证网络覆盖的情况下构造最优的连通支配集，这也是一个NP完全的问题。③拓扑生成。就是将节点按一定方式组织起来，协作地传输数据。比较典型的协议有基于簇的协议、基于链的协议和基于树的协议更迭逼近算法(IAA)［6］、延迟限定 － 最小生成树(DB-MDST)［7］等。其中基于树的协议经常被用于在持续性的监视应用中进行数据收集，是目前研究的热点。然而，IAA和DB－MDST等在构造生成树的过程中，树外节点是作为叶子节点被考虑并加入树的，在树没有最终建立前无法确定一个节点最终在树上拥有多少孩子。因此它们的生成树往往存在节点负载不均衡、树的高度无法控制的情况，这样不利于最大化树的生命周期，而且容易导致很大的延迟。在前人研究的基础上，提出了一个新的算法——DBDG，来构造一颗限定高度、负载均衡的生成树，从而有效满足延迟限定和网络生命周期最大化的要求。最后的仿真实验也验证了本文方法的有效性。

2 系统模型和问题描述

2.1 网络模型

n个传感器节点随机地分布在一个面积为M×M m2的正方形区域A内，存在1个Sink节点。整个传感器网络组成一个连通的无向图G(V，E)，其中V是节点集合，V={v0，v1，v2，…，vn}，|V|=n+1，其中v0是 Sink 节点，v1，v2，…，vn是传感器节点;E 是 G 中边的集合，如果2个传感器节点vi和vj相互处于对方的通信半径内，则(vi，vj)∈E。|E|=m为边的数量。网络具有如下性质:①网络是连通的静态网络，节点部署后不再移动;② 传感器节点的种类可以有多种，它们的初始能量是异构的，且不能补充。

2.2 相关定义

定义1:轮是从所有传感器节点收集一次数据，并传送到Sink节点的过程。

定义2:在一轮中节点vi在树T上的能量耗费S(T，vi)为:

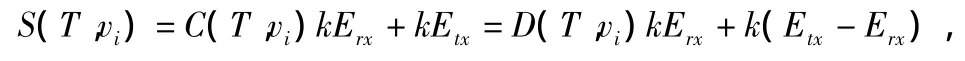
式中，C(T，vi)为节点vi在树T上孩子的数量;D(T，vi)=C(T，vi)+1为节点vi在树T上的度数。

定义3:节点的生命周期是节点vi在一棵树T中能存活的轮数。存活指节点vi的能量E(vi)＞0。节点vi在一棵树T中的生命周期可定义为:

定义4:树的生命周期是树T中第一个节点死亡时，该节点存活的轮数。定义为:

定义5:最优树是根据当前网络中所有节点的能量水平构造的一棵生成树，其生命周期比网络中其他生成树的生命周期都要大。定义为:

式中，T'为网络G中任意一棵生成树;TS(G)为图G中所有生成树的集合。

定义6:瓶颈节点是指一棵树中最早消耗完能量的节点，其生命周期与树的生命周期一致。

2.3 问题描述

在一些持续性的监视应用中，传感器网络的延迟与树的高度是密切相关的。此外，网络中节点的数量n等于树上各层节点孩子的总和，即

式中，h'为树高;hi为树上第i层所有节点的集合。根据式(3)，如果n是固定的，则树中每个节点的度越小，树的高度越大;反之，树高越小。因此，要得到越小的延迟，需要越小的树高，但是这样树上节点的度会比较大。

另一方面，根据式(1)和式(2)，生命周期最大的树可以表示为:

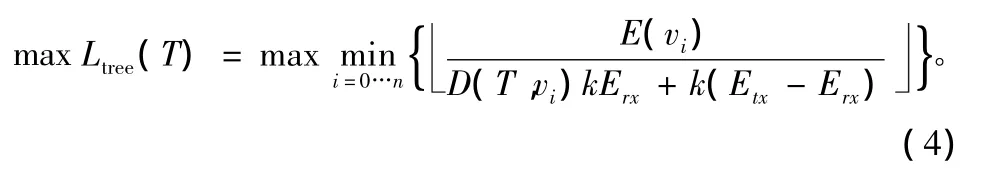
由于Erx和Etx是固定的，只有D(T，vi)可以调节，是主要的优化目标。为了简化表达，对式(4)进行等价变换:

式中，c=Etx/Erx－1。根据式(5)，要使树的生命周期最大，每个节点的度越小越好。但是根据式(3)这样会增加树的高度，加大时间延迟，与最小延迟的要求矛盾。因此，树的生命周期最大和最小时间延迟这两个目标是相互矛盾的，很难同时实现。因此，研究的问题是:在限定延迟的条件下，如何使得树的生命周期最大。

3 算法DBDG的设计

首先，利用网络G的拓扑构造一棵最少跳生成树T。方法为:先将图G中所有的边赋予相同的权值1，然后采用Dijkstra算法从Sink节点出发求解到各个节点的最短路径即可。树T肯定是网络G的所有生成树中最矮的，但是树上节点的度比较大。

接下来，以树T为基础进行优化，不断地将树上“瓶颈节点”的孩子转移到“非瓶颈节点”上去，以减小“瓶颈节点”的度(D(T，vi))。但是，D(T，vi)在式(5)中是式子的分母，并不容易进行调整。因此，将式(5)转换为如下等价的形式:

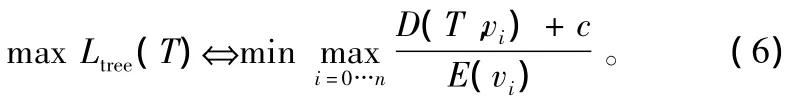
定义

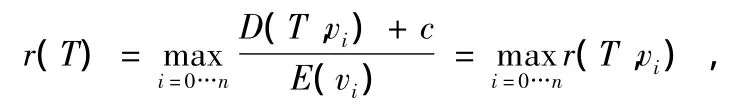
称为树T的最大反生命周期，r(T，vi)是树T上节点vi的反生命周期。这样，问题max Ltree(T)就转化为求树的最大反生命周期最小化问题，即

此外，要减少“瓶颈节点”的度，首先要明确哪些节点属于“瓶颈节点”。根据定义6，“瓶颈节点”是与树T的生命周期(或反生命周期)一致的节点。再观察式(6)，除去Sink节点，树T上节点反生命周期的最小变化幅度是δ=1/Emax，其中因此，根据反生命周期大小将树上节点划分到3个不同的集合V1、V2、和V3中:

① V1={vi|r(T)－δ＜r(T，vi)≤ r(T)，vi∈V}，在这个集合中节点的反生命周期与树T的反生命周期在同一区间内，属于“瓶颈节点”。

② V2={vi|r(T)－δ－1/E(vi)＜r(T，vi)≤r(T)－δ，vi∈V}，在这个集合中节点的反生命周期非常接近于“瓶颈节点”的反生命周期。如果它们的孩子增加一个，它们就会变为“瓶颈节点”。因此，称这个集合中的节点为“次瓶颈节点”。

③ V3=V－V1－V2，这个集合中节点的负载较轻，即使增加一个孩子也不会成为“瓶颈节点”，称为“富裕节点”。

接着，再定义算法DBDG中“优化”操作的含义为:在树T中针对某个节点x的优化，就是从图G中选择一条合适的边(u，v)加入树T并产生一个包含节点x的圈，接着再选择性地删除另一条在圈上且与x相连的边，使x的度减1同时产生的新树的高度不增长或者增长最小以不超过树高限定h。

由于节点能量的异构性，树中任何一个节点都可能属于“瓶颈节点”、“次瓶颈节点”或“富裕节点”中的一种。DBDG的主要目标是优化“瓶颈节点”，如果加入树的边(u，v)所依附的节点u和v都属于“富裕节点”，则优化操作可直接进行;如果加入树的边(u，v)所依附的节点u和v有1个或2个都属于“次瓶颈节点”，则优化操作不能执行。

综上所述，算法DBDG的描述如下:

输入:图G和树高限定h

输出:高度最多为h的最大化生命周期树

1.将图G中的边赋权值1，采用 dijkstra算法从v0出发构造一棵最小跳生成树T;

2.if(树T的高度 ＞ h)return false;

3.Ischanged=TRUE;

4.while(Ischanged)

5.{Ischanged=FALSE;LV1= Φ ;i=0;

6. FindEdge(T，LV1);

7. while(i＜Length(LV1))

8. {访问记录LV1［i］，将其包含的边(u，v)加入树 T中产生一个圈C;

9. for(圈C中的每一个“瓶颈节点”vj)

10. if(Optimal(vj，T)){Ischanged=TRUE;break;}

11. if(Ischanged)break;∥成功优化，进入下一轮迭代

12. 把边(u，v)从树T中删除;

13. i=i+1;

14. }∥while

15.}∥while

函数FindeEdge(T，＆LV1)的作用描述如下:

1.计算树T及其上所有节点的反生命周期，判断节点属于V1、V2或V3中的哪个集合;

2.T0←T;

3.将树T0中所有属于V1和V2的节点删除，得到一个组件的集合F;

4.for(图G中每一条连接不同组件的边(u，v))

5.{w(u，v)=level(T，u)+level(T，v);

6.根据权值 w(u，v)的大小，按递增的次序将记录(u，v，w(u，v))保存到表LV1中;

7.}

4 实验结果与分析

假设网络中所有节点随机地分布在一个200 m×200 m的正方形区域。每个节点的初始能量在［1J，1.5J］之间随机分布，节点的数据产生率为1 000 bits/round，Erx=50 nJ/bit，所有节点的最大通信半径为20 m。由于提出的数据收集方案是基于树结构的，因此选择基于树的算法FHT、IAA、DBMDST来进行对比。采用Matlab进行模拟实验。设定了2个实验场景:场景1中Sink节点位于区域的中心，坐标(50，50);场景2中Sink节点位于区域的边缘，坐标(100，50)。在2个场景中以50为增量，分批放置100～400个节点。分别观察各个算法的生命周期和生成树的树高，实验的结果是各个算法执行100次后的平均结果，如图1、图2、图3和图4所示。

图1 场景1中的生命周期对比

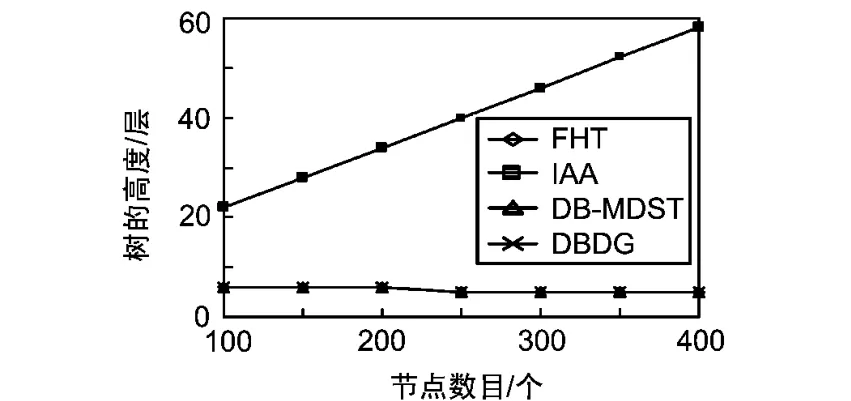
图2 场景1中的树高对比

图3 场景2中的生命周期对比

图4 场景2中的树高对比

由图1和图2可以看到在场景1中，不同的节点密度下，最少跳树FHT的生命周期最小，这是因为它虽然树高最小但树上节点的度很大，而且不能均衡节点的能量消耗。IAA树的生命周期最大，这是因为它没有高度限制，算法能对树上节点进行近似最优的优化。但是，IAA的树高明显比FHT的树高大很多。DB-MDST在与FHT同样树高的限制下，由于只对度最大的节点进行了部分优化，没有实现负载均衡，因此树生命周期比 FHT高，但是比DBDG低。

在图3和图4所示的场景2中，与场景1相比，FHT的平均生命周期增加了18%，IAA的平均树生命周期基本保持不变，DB-MDST的平均树生命周期增加了3%，DBDG的平均树生命周期增长了24%。这是由于Sink节点位于区域的边缘，使得位于区域另一端的节点到它的距离更远，需要更多跳才能到达。因此，FHT树的高度增加了(在场景1中是最大是6，在场景2中最大是9)。虽然FHT的树高增加了，减轻了对DB-MDST树高的限制，但DB-MDST的树生命周期并没有明显提高。与DB-MDST不同，FHT树高的增加和节点度的减少，都有利于DBDG进行优化操作，使其生成树的生命周期有较大提高。因此，DBDG在低节点密度(100个和150个)时做到了与IAA相同的优化程度。只在节点密度增加后，其树的生命周期才逐渐下降。综上所述，DBDG在各种条件下均优于DB-MDST和FHT。

5 结束语

无线传感器网络在工作过程中，节点会不断地感知到周边环境的数据。而在无线传感器网络任何一个应用中，用户都需要获取相应的数据进行处理。采集网络中用户需要的数据，就被称为数据收集。数据收集是无线传感器网络中最重要的操作之一，能否有效地采集到合适的数据，直接关系到应用的效果。针对目前的数据收集方法造成的能量浪费和网络传输延迟较大的问题，提出了一种限定延迟的算法DBDG，并通过仿真实验验证了本文方法的有效性。下一步工作主要研究密集部署网络中的生命周期最大化问题。

［1］李方敏，徐文君，刘新华.无线传感器网络功率控制技术［J］.软件学报，2008，19(3):716 －732.

［2］GAO Yan，HOU Jennifer，NGUYEN Hoang.Topology Control for Maintaining Network Connectivity and Maximizing Network Capacity under the Physical Model［C］∥Proc.of the IEEE 27th Conference on Computer Communications(INFOCOM2008)，2008:1 013 －1 021.

［3］AMMARI H M，DAS A K.A Trade-off between Energy and Delay in Data Dissemination for Wireless Sensor Networks Using Transmission Range Slicing［J］.Computer Communications，2008，31(9):1 687 －1 704.

［4］KIM Joohwan，LIN Xiaojun，SHROFF N B，et al.On Maximizing the Lifetime of Delay-sensitive Wireless Sensor Networks with Anycast［C］∥Proc.Of The IEEE 27th Conference on Computer Communications(INFOCOM2008)，2008:807－815.

［5］COHEN R，KAPCHITS B.An Optimal Algorithm for Minimizing Energy Consumption while Limiting Maximum Delay in a Mesh Sensor Network［C］∥Proc.of the IEEE 26 th Conference on Computer Communications(INFOCOM2007)，2007:258－266.

［6］WU Yan，FAHMY S，SHROFF N B.On the Construction of a Maximum-Lifetime Data Gathering Tree in Sensor Networks:NP-Completeness and Approximation Algorithm［C］∥Proc.Of The IEEE 27th Conference on Computer Communications(INFOCOM2008)，2008:356 －360.

［7］KWON Soonmok，KIM Jeong-gyu，KIM Cheeha.An Efficient Tree Structure for Delay Sensitive Data Gathering in Wireless Sensor Networks［C］∥Pro of 22nd IEEE International Conference on Advanced Information Networking and Applications，2008:738 －743.

［8］CORMEN T，LEISERSON C，RIVEST R，et al.Introduction to algorithms［M］.McGraw-Hill，2001.