基于RO模型的公钥加密方案安全性分析与证明

黄贻望 袁科,2 杨英杰

1铜仁学院数学与计算机科学系 贵州 554300 2南开大学信息技术科学学院 天津 300071

0 引言

密码方案或协议的安全性证明在设计阶段又是很难做到的，基于此目前普遍做法是，提出一种方案或协议后，根据某种困难性假设，做出具体的安全性分析，然后给出其安全性论断：如果在一段时间内找不到该方案协议的漏洞，则接受其安全性论断；否则，加以修正以继续使用，直至超出应用所能承受的代价。可证明安全性理论方法是首先确定所设计的方案或协议安全性目标和攻击敌手模型，通过敌手在多项式时间内成功破解的概率优势是可以忽略的，从而给出其安全性证明，通过可证明安全性方法得到证明的方案或协议可以防止一些未知的攻击。

1 随机预言模型可证明安全及归约论断

一个典型的RO模型首先确定安全目标和敌手模型，因此，实现可证明安全性的首要工作是在为密码体制确定合适的安全性目标，由于密码体制因应用要求不同而有所侧重，大致分为加密安全性和签名安全性：

1.1 安全性目标

加密方案的安全目标：

(1) 单向性：由密文不能恢复相应的明文。

(2) 不可区分性：对敌手给定的两个明文，加密者随机选择其中一个进行加密，敌手无法从密文中知道是对哪个明文的加密。

(3) 语义安全性：敌手在知道密文的情况下，能计算出明文的信息量并不他在不知道密文的时候多，除了明文长度。

(4) 不可延展性：敌手无法构造与已给密文有关系的新密文。

(5) 明文可意识性：敌手不能以一个不可忽略的概率，在不知道明文的情况下，构造一个密文。

1.2 敌手模型定义

加密方案的敌手攻击类型有：

(1) 选择明文攻击(CPA)：敌手可加密所选的任何明文，获得相应的密文。

(2) 非适应性选择密文攻击(CCA1)：敌手在得到挑战密文C*之前可以选择密文询问解密机，以获得相应的明文，但在得到C*后就不再询问解密机。

(3) 适应性选择密文攻击(CCA2)：敌手在得到挑战密文C*前后都可以询问解密机，以获得相应的明文，但在得到C*后，不能询问C*的明文。

对于加密方案，目前接受的安全性是适应性选择密文攻击下的不可区分性(IND—CCA2)，所以具有语义安全的加密方案是指该方案具有IND—CCA2安全性。

其安全性证明可以用以下的对局实现：

(1) 密钥生成器生成系统的公钥和私钥，公钥向敌手公开而私钥对其保密。

(2) 敌手A选择密文解密机进行一系列的询问，对每一个询问解密机用私钥解密并将解密结果给敌手。敌手可以任意的方式构造这些密文，不一定用加密算法来构造。

(3) 敌手A也可以对加密机进行一系列的询问。敌手选择两长度相同的消息M0和M1交给加密机，该加密机随机选b∈R{ 0,1}，然后对Mb进行加密得到密文Cb*交给敌手A。

(4) 敌手A仍然可象第(2)步一样向解密机提出新的询问，但他不能询问目标密文Cb*。

(5) 敌手A输出b'∈ { 0 ,1}，表示它对b的猜想，如果b=b'，则敌手赢得对局。

在对局中，敌手A的优势(Advantage)定义为概率

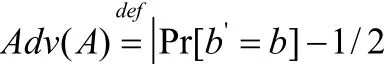
称一个公钥加密体制是IND—CCA2安全的，是指对于任意的多项式时间敌手A，它的优势是可以忽略的。

1.3 RO模型介绍

完整的RO模型：假定各方共同拥有一个公开的Random Oracle就可以构建一个安全协议P，首先在RO模型中证明PR，然后用函数h取代Oracle。需指出的是，这种模型的可证明安全性并非严格意义上的。

假设我们提出一个协议问题∏(这个问题和h函数“独立”)，要设计一个安全协议P解决该问题，可按如下步骤执行：

(1) 建立∏在RO模型中的形式定义，RO模型中各方(包括敌手)共享随机OracleR；

(2) 在RO模型中设计一个解决问题∏的有效协议P；

(3) 证明P满足∏的定义；

(4) 在实际应用中用函数h取代R。

1.4 归约论断及其安全性

在RO模型中的归约论断一般表现为：首先形式化定义方案的安全性；假设PPT敌手能够以不可忽略的概率破坏协议的安全性(如伪造签名)；然后模仿者S(就是设计者或分析者)为敌手提供一个与实际环境不可区分的模拟环境(RO模型)，回答敌手的所有Oracle询问(模拟敌手能得到的所有攻击条件)；最后利用敌手的攻击结果(如一个存在性的伪造签名)设法解决基础难题，如果把RO模型换成现实模型就得到标准安全性证明。

归约论断的思想：(1)指明问题P1的难解性意味着另一个问题P2的难解性；(2)求解P2的算法可以用来求解P1。

具体安全性处理的一个重要目标就是：在把一个基本原子命题转化成相应协议时，尽可能多地表现原子的强度，这表现为要求“紧”的归约方法，因为一个“松”归约意味着要求采用更长的安全参数，从而降了效率。

2 公钥加密方案的可证明安全性分析与证明

可证明安全理论能够保证密码方案或协议在某种强度下的安全性，能够预防未知的攻击，因此，成为现代密码学一个热点研究方向，许多密码学者做出一些相关的可证明安全方案或协议，这里仅就RO模型下的满足选择密文安全性的加密方案(BR)作简要说明。

2.1 RO模型下的IND-CCA2安全性证明思想

由前面可得到如图1所示的公钥加密的RO模型。

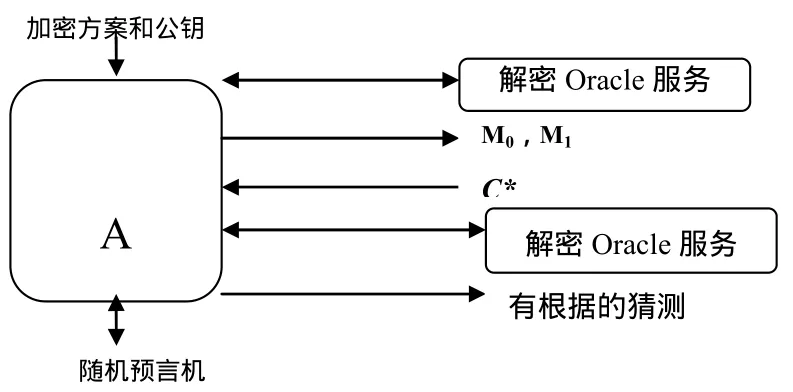
图1 加密RO模型

假设有个具有一定优势的敌手 A，则得到它的攻击 RO模型如图2所示。

图2 攻击RO模型

2.2 BR方案的IND-CCA2安全性证明

2.2.2 BR方案的IND—CCA2安全性证明

选择密文安全性证明(IND-CCA2)：假设存在优势为λ(k) 的IND—CCA2敌手，构造算法M，任意给定y，M的目标是求解f-1(y),步骤如下：

(1) 在find-stage，M仿真oracle G，H和DG，H；M回答解密询问a| |w||b方法；如果A做过G询问r和H询问ru且满足于a=f(r)andw=G(r) ⊕u，则返回u，否则返回“无效”。

(2) 当A选择 (m0,m1) 后，M选择密文a←y||w||b，其中w和b随机选择。

(3) 在guess-stage，M以同样的方式仿真oracleG,H和DG,H；若有G询问r满足f(r) =y；此明M就会成功。若为了使 A感觉不到欺骗，M可以计算G(r) =w⊕mb*,H(mb*) =b,b*是抛币的结果。

(4) 令事件Ak表示 A 能构造密文a| |w||b仅当A提过r的G询问或ru的H询问，其中r满足a=f-1(r)。令事件Lk表示a| |w| |b(满足b=H(f-1(a) | |w⊕G(f-1(a))))的DG,H询问，但从未提出过关于f-1(a) | |w⊕G(f-1(a))的H询问。令n(k)表示A提出的询问总次数，k是安全参数，显然是有Pr[Lk] ≤n(k) · 2-k，容易看出：A有成功优势当且仅当事件 Ak或Lk发生，即Pr[Asucc[Lk∧Ak]=1/2，故

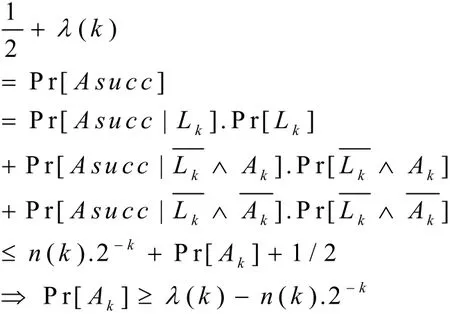
注意到事件 Lk则M将会失败，故Pr[Mi n vertf]≥λ(k) -n(k)·2-k，因此方案具有选择密文的安全性。

3 结语

可证明安全性理论是基于一定的基础假设的选取，因此安全强度依赖于某一假设为基础，因此，假设越弱的安全性证明越可靠。同时，两种可证明安全性模型相比较，随机预言(RO)模型尽管是在一定的条件下的安全性，但是具有重要实际应用价值；而标准模型的可证明安全性由于实现的代价大，因此，适应于理论分析。

[1]Bellare M. Practice-Oriented provable-security.In: Damgard I,ed.Modern Cryptology in Theory and Practice.LNCS 1561,Berlin,Heidelberg:Springer-Verlag.1999.

[2]Goldreich O.Foundations of Cryptography.Cambridge:Cambridge University Press.2001.

[3]Goldwasser S, Micali S. Probabilistic encryption. Journal of Computer and System Science.1984.

[4]Goldwasser S,Micali S,Rivest R.A digital signature scheme secure against adaptive chosen-message attacks.SIAM Journal of Computing.1988.

[5]Bellare M,Rogaway P.Random oracles are practical:A paradigm for designing efficient protocols.In: Proc.of the 1st ACM Conf. on Computer and Communications Security.New York:ACM Press.1993.

[6]张文政.公钥密码密码体制可证明安全性的几点注记[J].信息安全与通信保密.2005.

[7]冯登国.可证明安全性理论与方法研究[J].软件学报: Vol.16,No.10.