一种基于聚集系数的复杂网络社团划分算法

王学凯 马英红

山东师范大学管理科学与工程学院 山东 250014

0 引言

复杂网络的特征和性质在近些年来已经成为研究的热点。对社团结构的研究对于理解和分析网络结构及其功能有着至关重要的作用已广泛应用到生物学、计算机科学、社会学等领域中。社团结构是指其社团内部节点连接紧密，社团之间连接相对稀疏的一种结构。许多研究人员从不同角度出发提出了划分社团算法，例如Kernighan-Lin算法，Kernighan算法是一种基于贪婪算法原理将网络分割为两个大小已知的社团的二分法，但该算法必须已知网络社团的确切规模才能得以应用；基于Laplace图特征值的谱平分法，利用网络结构的Laplace矩阵中不为零的特征值所对应的特征向量，和同一个社团内的节点对应的元素近似相等的原理对网络社团进行划分，在规模为n个节点的网络中，该算法的复杂度为O(n3)；GN算法通过从网络中移除介数最大的边将整个网络分成越来越小的部分，其不足在于对网络社团划分优劣没有一个定量描述。Newman等人经过研究提出了一种度量网络社团划分质量的标准，成功地解决了这个问题。Wu和Huberman提出了基于电阻网络电压谱的快速分割算法，该方法须已知分属于不同社团的两个节点。Newman义了模块度Q，用来衡量网络划分质量，Q值越大，说明划分结果越好。Clauset等通过节点的局部信息，提出局部模块度，该方法的优点是计算量比较小。在很多情况下，研究人员关注的是网络的局部社团结构。例如，在社会网络中搜索时通常只关心某个人所在的社团，此时就不需要耗时寻找网络的全局社团结构，而只需搜索网络中某个节点所在的局部社团。

本文提出一种局部社团划分的新算法，通过搜索邻居节点以及计算有关节点聚集系数，选择符合条件的节点加入局部社团，最终获得待求节点所在的社团。局部社团对邻居节点的吸引力取决于社团对该节点的重要程度。节点的聚集系数就是表征某节点邻居之间连接的紧密程度，因此通过考察某局部社团存在前后其邻居节点聚集系数的变化情况来确定社团和节点之间的关系。利用该算法寻找到某个节点的社团后，从网络中社团外的任一节点开始寻找其社团，重复此过程，即可得到网络的全局社团结构。

1 相关概念

在一个无向无权网络G=＜V,E＞中，具有n个节点，m条边，eij表示节点i和节点j之间的连边，V={i|i∈n}，E={eij|i,j∈n且i≠j} 。

(1) 邻居节点集合

节点i的邻居节点集合：Ni={j|节点i和节点j 直接相连}；社团Ψ的邻居节点集合：

n表示社团Ψ具有的节点的个数。

(2) 聚集系数

① 节点的聚集系数

节点i的聚集系数Ci定义为：Ci=Ei/Ti,,Ci∈[0,1]。

其中，设节点i的度是ki，Ei表示节点i的k个邻居节点之间实际的连接边数，Ti表示节点i的k个邻居节点之间可能形成的最大连接数，Ti=ki(ki-1)/2。当Ci=1时，表示节点i的所有邻居节点之间都相互连接，节点i和它的邻居节点之间形成了全局耦合网络，连接紧密。

② 边的聚集系数

边eij的聚集系数：Ci,j=|Nij|/(ki+kj-|Nij|-2)，

式中Nij=Ni∩Nj，表示节点i和节点j的公共邻居集合，|Nij|表示以eij为边组成的实际三角形的数量。边的集聚系数Ci,j∈[0,1]，它表示被这条边所连接的两个节点的连接强度，值越大，强度就越强，表示这两个节点在同一个社团的可能性就越大。

(3) 社团的度

在社团Ψ 中，Din(Ψ)表示社团的内度，Dout(Ψ)表示社团的外度，n表示社团Ψ内节点的个数，表示节点i和社团Ψ内部节点连接度，表示节点i和社团Ψ外部节点连接度，其中对∀i∈Ψ。

① 社团的内度

社团Ψ的内度为：

② 社团的外度

设社团Ψ的外度为：

③ 节点的内外度差：

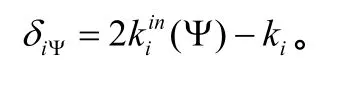
2 算法描述

本文提出的算法从待求节点开始到最终划分出全部社团为止。首先将待求节点加入到一个空社团，即得到一个局部社团，通过邻居节点的度和聚集系数等相关比较计算，不断地添加邻居节点，直到发现没有符合条件的节点时，即刻停止便可获得一个社团。在剩余网络中重复运行，最终将网络划分为若干个社团。为方便算法的描述，在确定社团时可以根据以下定义提出以下约定：

(1) 若社团外的某一节点i有一半以上连接与该社团相连，那么这个节点也在社团中。

(2) 在与社团连接的所有边中，若存在一条边eij满足以下条件，那么节点j也属于该社团。该条件是边eij的聚集系数是在与社团连接的所有边中是最大的，其中节点i是该社团内的一点，j是该社团的邻居节点，并且与节点j相连的其它边的聚集系数小于等于该边的聚集系数。

(3) 要求社团的内度大于社团的外度。

(4) 计算所形成初步社团中每一个节点的内外度差，优化社团结构。

具体算法过程如下描述：

输入：一个无向无权网络G=＜V,E＞，V是网络中节点集合，E是网络中边的集合。

输出：网络的社团结构。

① 初始社团Ψi为空。

② 选取剩余网络中度数最大的节点i作为社团Ψi的初始节点。令Ψi←Ψi+i ，V←V-i，建立社团Ψi的邻居集合NΨi。

③ 计算社团Ψi的邻居集合NΨi中的每个节点的度，如果节点的度有一半或者以上的与社团Ψi相连，将把这些节点并入到社团中；在剩余的邻居节点中计算每个节点与社团连接边的聚集系数，找到与边的聚集系数最大的对应的那个邻居节点并计算与该节点连接的其他边的聚集系数，比较与社团连接的聚集系数，如果与社团连接的聚集系数是最大的，那么将该节点加入到社团中，否则，计算找到聚集系数为第二大、第三大...的边，并计算与该边对应的邻居节点连接的其他边的聚集系数，如果是最大加入社团中，直到没有符合条件的节点为止。Ψi←Ψi+Vi，V←V-Vi，并更新邻居集合NΨi，直到Ψi的邻居集合中不再有新的节点加入。重复②③形成所有社团结构。

④ 比较③中形成的社团的内度和外度，如果内度大于外度，则进行步骤⑤，否则将小度社团与邻居社团中内度最大的社团合并后进行步骤⑤。

⑤ 计算所形成的初始社团中每一个节点的内外度差δ，如果δ≤0，计算该节点的邻居节点属于不同社团的邻居数并加入具有最大邻居数的社团；如果δ＞0，则节点所属的社团不变。

⑥ 输出所有社团。

3 实验与分析

为了验证该算法的可行性以及划分的精确性，本次试验选择了Zachary空手道俱乐部成员网络和Dolphin social network经典网络进行划分。

(1) Zachary空手道俱乐部成员网络

Zachary空手道俱乐部网络是复杂网络在社会学分析中常用的经典问题之一。20世纪70年代初，Zachary用了两年时间观察美国一所大学空手道俱乐部成员间的相互社会关系，基于这些成员在俱乐部内部和外部的社会关系，Zachary构造了该网络。Zachary空手道俱乐部网络由34个节点和78条边组成，节点代表俱乐部的成员，边代表成员之间的关系。将本文提出的算法应用于该网络，得到的划分结果如图1所示。

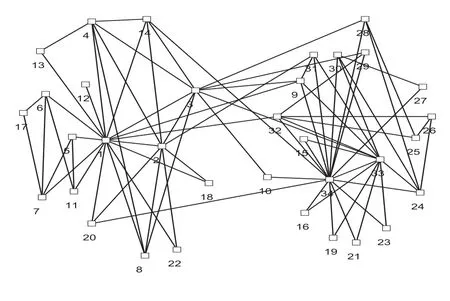
图1 Zachary俱乐部网络

(2) Dolphin social network网络

Lusseau在1994年-2001年研究了生活在新西兰的62只海豚，通过观察它们之间的联系情况，构建了海豚社会网络。在他观察期间，随着一只关键海豚的离开，这个群体分成了两个小群体，利用本文中的算法将该网络划分成3个社团结构，图2是利用本文的算法对该网络划分的结果。

5 结术语

复杂网络社团研究中，存在着许多种社团发现的算法，本文提出了一种基于聚集系数的局部社团划分最终求出整个网络的社团划分，该算法用时少，划分准确，并通过实验得到的理想结果证明其划分的准确性，该算法同样可以应用于数据挖掘的多个领域，在今后的研究中，应结合新的理论成果和技术方法寻找新的更有效的算法。

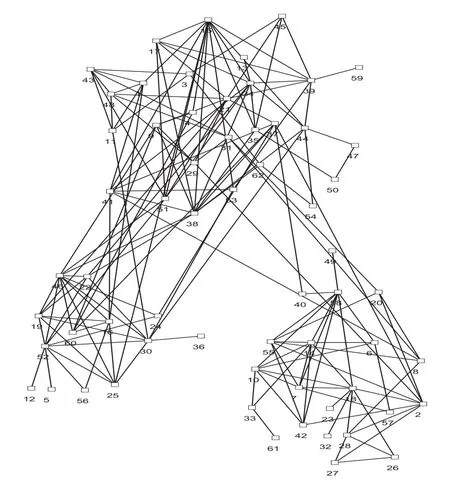
图2 海豚网络的社团结构

[1] Kernighan B W, Lin S. An efficient heuristic procedure for partitioning graphs[J]. Bell Syst Tech J.1970.

[2] Kleinberg J. Authoritative sources in a hyperlinked environment[J].JACM.1999.

[3] Girvan M, Newman M E J. Community structure in social and biological networks[J].Proc Natl Acad Sci USA.2002.

[4] Newman M E J, Girvan M. Finding and evaluating community structure in networks[J].Phys Rev.2004.

[5] Wu F, Huberman B A. Finding communities in linear time： A physics approach[J]. Eur Phys J B, 2004.

[6] Newman M E J,Girvan M. Finding and evaluating community structure in networks[J].Phys Rev.2004.

[7] Clauset A, Newman M E J, Moore C. Finding community structure in very large networks[J].Phys Rev.2004.

[8] Zachary W. An information flow model for conflict and fission in small groups[J].J Anth Res.1977.

[9] Lusseau D, et al. The bottlenose dolphin community of doubtful sound features a large proportion of long-lasting associations, can geographic isolation explain this unique trait[J].Behavioral Ecology and Sociobiology.2003.