针束型回热器熵产率的分析

杨志春，吴 锋, 余仕成

(1. 海军驻武汉438厂军事代表室，湖北 武汉 430064；2.武汉工程大学理学院，湖北 武汉 430074)

0 引 言

热声发动机和制冷机没有或者很少有运动部件，并且使用环境友好气体作为工质，以上突出优点使其在近年来备受关注[1].回热器是热声热机的关键部件[2-3]，实际热声装置中使用了多种结构形式的回热器包括平行板结构、圆孔结构和钢丝型结构等[4-5].Swift等[6-7]引入了一种被称为针束结构的新型回热器：针束型结构如图1所示，在回热器轴向位置平行布置多根细针，单根针半径为rd，每根针处于一个正六边形流道中心.理论与实验均已证明针束型回热器结构优于其它规则几何结构的回热器[8].

图1 针束结构回热器横截面局部示意图Fig.1 A schematic diagram of the pin-array stack

工质在回热器内振荡时的换热和黏性损耗会导致不可逆损失，这种不可逆损失可以通过熵产率[9-10]来分析.文献[11-16]对热声装置不可逆性进行了分析，但这些研究仅仅集中于单板、平行板或钢丝型回热器以及换热器.本文对针束回热器中由换热和黏性耗散导致的熵产率进行了分析，研究了间距、尺寸、角频率、温度梯度和阻抗比等参数对熵产率的影响.

1 理论分析

线性化动量守恒方程为[4]

(1)

在无滑边界条件下，有：

u1(rd)=0

(2)

在针的表面，对称边界条件下：

(3)

连续性方程为：

(4)

其中cp为工质的复密度振幅.

线性化能量方程为：

(5)

其中cp为比定压热容，T1为复温度振幅，dT/dx为温度梯度，T0为平均温度，β为等温膨胀系数，k为工质导热系数.

线性化状态方程为：

(6)

其中a为工质绝热声速，γ为比热比.

由公式(1)-(6)可得：

(7)

(8)

其中

(9)

(10)

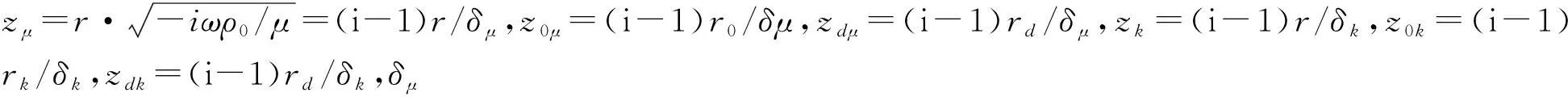
单位质量工质能量方程为

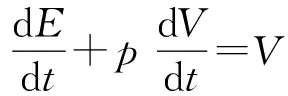
(11)

由傅里叶导热定律

(12)

可得：

-[T⊥T)2]

(13)

将公式(11)代入(5)得：

(14)

将Gibbs 方程Tds=dE+pdV代入公式(14)并忽略一阶小量得：

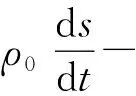
(15)

其中s为单位体积熵产.

公式(15)左边第一项为单位体积熵产率，第二项为熵流.公式(15)右边第一项为黏性不可逆性引起的熵产率，第二项为传热引起的熵产率.由此可得单位体积熵产率：

(16)

在层流和小扰动条件下，黏性耗散函数为：

ø=μ(⊥u1)2

(17)

将公式(17)代入公式(16)并取时间平均得：

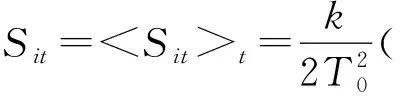
(18)

其中*表示复共轭.

将公式(7)和公式(8)代入公式(18)并取实部可得针束型回热器时均熵产率：

(19)

其中

由公式(19)可知Sir与r有关，即Sir沿流道横向截面有一分布，取其截面平均得：

(20)

其中

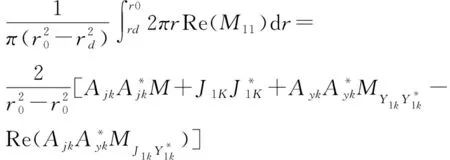
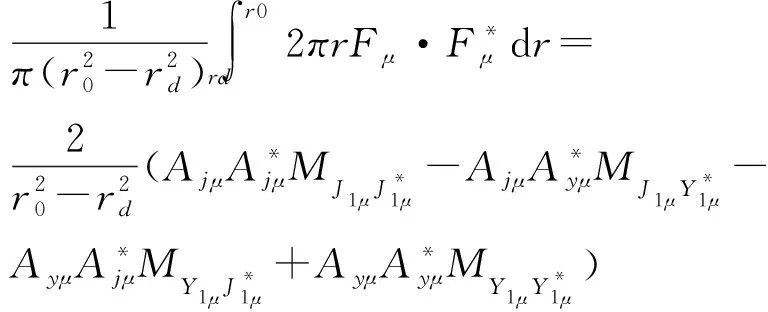
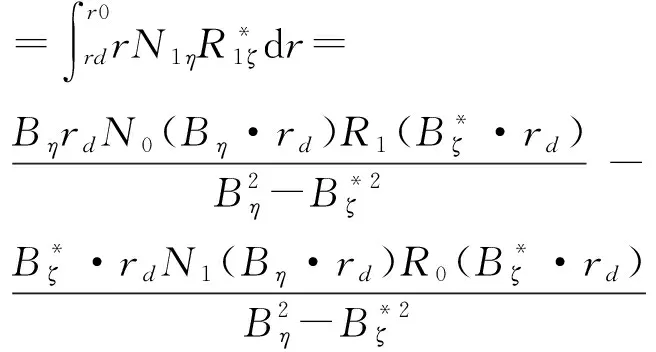
(N,R=J,Y;η,ζ=μ,k)

2 数值结果分析

根据公式(19)和(20)，可分析得出不同参数对熵产率的影响：

2.1 截面分布熵产率

公式(19)表明截面分布不可逆熵产率Sir是针束距中心点距离r的函数.计算时所取参数T0=600 K,T0β=1,f=ω/2π=400 Hz,dT/dx=1 000 K/m,Z=1,rd=0.000 1 m,ρ0=1.9 kg/m3,σ=0.68和k=0.13W/(m2·K).由图2可知：在不同的r0/rd下Sir随着r的增大而减小.这是因为离针束越远，换热与黏性耗散的程度越小，回热器的不可逆性越小.

图2 熵产率的截面分布Fig.2 Cross-section entropy generation rate distribution

2.2 温度梯度对截面平均分布熵产率的影响

取参数T0=600 K,T0β=1,f=ω/2π=400 Hz,Z=1,rd=0.000 1 m，ρ0=1.9 kg/m3,σ=0.68和k=0.13 W/(m2·K)，如图3所示：在不同r0/rd时Sir随温度梯度dT/dx的增大而增大，这是由于换热导致的不可逆性受温度梯度影响.

图3 截面平均熵产率随温度变化规律Fig.3 Cross section average entropy generation rate versus temperature gradient

2.3 针束型回热器的优化频率

给定特征尺寸r0/δk和rd/r0时，当角频率ω变化时，存在最小截面平均熵产率Si.由公式(20)，当∂Si/∂ω=0时可得：

(21)

ω0为截面平均不可逆熵产率最小时的优化角频率.计算时取参数T0=600 K,T0β=1,dT/dx=1 000 K/m,Z=1,rd=r0/5,ρ0=1.9 kg/m3,σ=0.68和k=0.13 W/(m2·K)，在不同r0/rd时Sir随ω的变化规律如图4所示.

图4 截面平均熵产率随角频率的变化规律Fig.4 Cross section average entropy generation rate versus the circular frequency

优化频率f0经计算可得：

2.4 针束型回热器的优化阻抗比

取参数T0=600 K,T0β=1,f=ω/2π=400 Hz,dT/dx=1 000 K/m,rd=0.000 1 m,ρ0=1.9 kg/m3,σ=0.68和k=0.13 W/(m2·K)，在不同r0/rd时Sir随阻抗比Z的变化规律如图5所示.当Z变化时存在最小Si，对应的最优Z为：

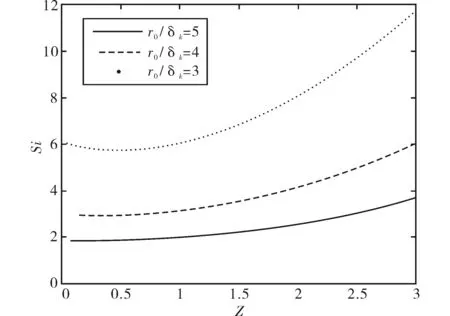
图5 截面平均熵产率随阻抗比的变化规律Fig.5 Cross section average entropy generation rate versus impedance ratio

3 结 语

本文对针束型回热器中由于换热和黏性耗散的不可逆性导致的熵产率进行了研究，计算获得了截面熵产率的分布.在给定参数下，截面平均分布熵产率随温度梯度的增大而增大，随阻抗比变化时存在最小值.给定特征尺寸时，获得了最小熵产率对应的最优频率.本文结果有利于选择针束型回热器的优化尺寸.

参考文献：

[1] 吴锋, 李青, 郭方中, 等. 热声理论的研究进展[J]. 武汉工程大学学报, 2012, 34(1): 1-6.

[2] Swift G W. Thermoacoustic engines[J]. J Acoust Soc Am, 1984, 84(4): 1145-1180.

[3] Tominaga A. Thermodynamic aspects of thermoacoustic theory[J]. Cryogenics, 1995, 35(7): 427-440.

[4] Hofler T J. Thermoacoustic refrigerator design and per-formance[D]. San Diego: Physics Department, University of California at San Diego, 1986.

[5] Swift G W. Analysis and performance of a large th-ermoacoustic engine[J]. J Acoust Soc Am, 1992, 92(3): 1551-1563.

[6] Swift G W, Keolian R M. Thermoacoustics in pin-array stacks[J]. J Acoust Soc Am, 1993, 94(2): 941-943.

[7] Hayden M E, Swift G W. Thermoacoustic relaxation in a pin-array stack[J]. J Acoust Soc Am, 1997, 102(5): 2714-2721.

[8] Gibson R J, Nessler F S, Keolian R M. Measurements of a thermoacoustic pin stack[J]. J Acoust Soc Am, 1996, 100(4): 2735-2742.

[9] Bejan A. The thermodynamic design of heat and mass transfer processes and devices[J]. Heat and Fluid Flow, 1987, 8(4): 398-406.

[10] Bejan A. Entropy generation through heat and fluid flow[M]. New York: Wiley, 1982.

[11] Shohel Mahmud, Roydon Andrew Fraser. The Ther-moacoustic irreversibility for a single-plate thermoa-coustic system[J]. International Journal of Heat and Mass Transfer. 2006, 49: 3448-3461.

[12] Hadi Babaei, Kamran Siddiqui. Design and optimiz-ation of thermoacoustic devices[J]. Energy Conver-sion and Management, 2008, 49: 3585-3598.

[13] Ishikawa H, Hobson P A. Optimisation of heat excha-nger design in a thermoacoustic engine using a second law analysis[J]. Heat mass transfer, 1996, 23(3): 325-334.

[14] 吴锋, 陈林根, 孙丰瑞,等.斯特林机的有限时间热力学优化[M]. 北京: 化学工业出版社, 2008.

[15] 余仕成. 平板型回热器的不可逆熵产率分析[J]. 武汉化工学院学报, 1999, 21(2): 85-89.

[16] 余仕成, 王克协, 吴锋. 钢丝型回热器的不可逆熵产率分析[J], 吉林大学自然科学学报, 1999, 3: 52-56.