基于M allat算法的小波分解重构的心电信号处理

钟丽辉，魏贯军

（1.西南林业大学 云南 昆明 650224；2.郑州大学 河南 郑州 450001）

由于心电信号微弱（mV级）；超低频，心电的主要成份<50 Hz；并且信噪比低，同时在采集过程中常常掺杂各种噪声和干扰。所以对心电信号的预处理对心脏疾病的客观诊断具有重要意义。现代信号处理技术的发展推动了生物医学信号处理方法的更新。在传统的傅立叶变换基础上产生的小波变换由于具有多尺度多分辨率的优异特性，因此非常有助于心电信号的处理。

由于心电信号属于微弱的电信号，而且采集过程受多种噪声干扰，特别是干扰中的肌电干扰跟心电信号的频谱有部分的重叠，普通的频带滤波无法滤除频率重叠部分的噪声，所以心电信号的去噪处理成为目前研究的热点和难点。在文献[1]中，采用小波阈值法对心电信号进行去噪，主要去除白噪声型的干扰；在文献[2]中，采用小波熵的对心电信号去噪，主要去除高频干扰；在文献[3]中，结合小波分解和小波阈值处理心电信号，虽然能同时去除多种噪声，但是该算法导致心电信号产生吉布斯现象；在文献[4]中，采用自适应小波阈值算法仅去除了心电中肌电干扰；在文献[5]中，采用卡尔曼滤波去除心电倒相中的畸变和白噪声。在实际应用小波分析去噪过程中，怎样去除多种干扰，并不已损耗心电信号有用特征为前提，同时算法运算速度快等问题需要进一步探讨。

笔者采用Mallat算法的小波分解重构法对MIT-BIT心律失常数据库的心电记录进行仿真。首先确定小波分析的小波基；其次确定小波分解的层数；然后直接提取心电信号特征波所在的频带进行重构，最后Matlab仿真结果表明小波分解重构法成功的实现了心电信号中的基线漂移和肌电干扰的去除；同时该算法运行速度快，使用比传统的滤波器方便。

1 小波分析M allat算法

由于低信噪比心电信号的特征波与部分干扰信号（肌电干扰）的频带相互重叠，普通的频带滤波方法不能将两者分开。小波变换由于具有良好的时频局部化特性，同时小波理论研究的不断深入，非常有助于心电信号的处理。

设 WM为 VM在 VM-1中的补空间，即 VM-1=VM⊕WM，WM⊥VM，则 {WM}构成一组相互正交的子间序列，即∀M≠N有WM⊥WN，并且 L2（R）=Wj。

设多尺度分析的生成元为 φ（t），若〈ψ（t-k）；k∈z〉构成W0中的一组标准正交基，则尺度函数φ（t）和小波函数V（t）满足以下双尺度方程[6]：

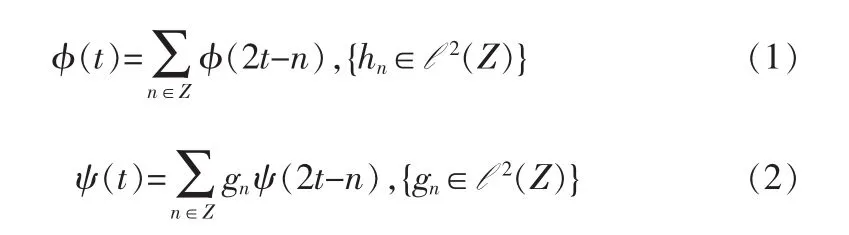
则信号分解和重构的Mallat算法如下：

1）分解算法

对任意的 f（t）∈L2（R），设存在{}n∈Z∈l2，使得

2）重构算法

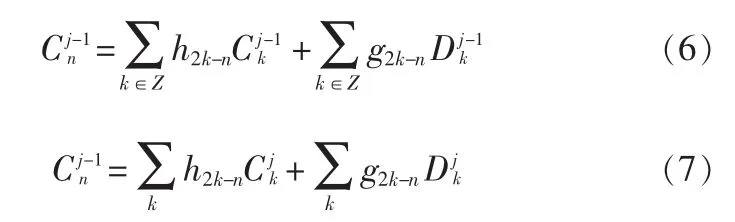
尺度函数和小波函数的傅里叶变换具有低通和带通滤波器的性质，所以小波的多尺度分析可以看做相应信号频段的低通和高通滤波。本文心电信号的处理中仅仅用到了分解和重构的马拉算法。

2 文中算法的实现

小波分解与重构是一种原理简单的小波去噪方法，它主要是利用小波的多分辨率分析特性对带有基线漂移和肌电干扰的心电信号按照采样频率进行分解，将不同频率组成的含噪心电信号分解成不同频带的子信号，然后对含有心电信号特征波的频段给予保留，其他的频段直接置零来进行去噪。

2.1 文中方法去噪的实现

1）确定心电信号去噪的小波基[7]

文中小波基的选择是根据小波函数的数学特性和小波的尺度函数。Sym8小波函数的数学特性为正交但不严格对称；Sym8小波的尺度函数很接近心电信号的特征波段，所以本文选用sym8小波对心电信号进行去噪处理。

2）确定心电信号的分解层数

文中利用心电信号、基线漂移和肌电干扰的频率范围确定分解层数。心电信号的QRS波群的频率范围为3～40 Hz；P、T波的频率范围为0.7～10 Hz。常见的心电干扰中的肌电干扰频率在5～2 000 Hz之间；基线漂移一般频率<1 Hz。文中的分解层数为8层。

3）将基线漂移的低频段和肌电干扰的高频段置零。

4）用剩下的频段对心电信号进行重构，重构的信号就是去噪后的心电信号。

2.2 M atlab实验结果

文中实验数据来自采用MIT－BIT心律失常数据库的心电记录。MIT－BIT标准数据库中的心电信号采样频率为fs=360 Hz，以下实验给出的图表是103号心电数据仿真的结果。截取103号心电信号的一段进行研究，起始时间为20 s，取信号长度为N=2 048点。因为103号记录的心电信号所含噪声比较少，属于比较干净的数据，为了更好的观察本文方法的去噪效果，在该段心电信号上叠加了均值为0，方差为QRS波峰0.02倍的高斯白噪声和周期为2 s，峰值为心电信号最大峰值的0.2倍的正弦信号来模拟肌电干扰和基线漂移。

采用Sym8小波分解含噪心电信号八层后的通带频率如表1所示（CAi和CDi表示第尺度下的逼近信号和细节信号）。

表1 小波分解后的通带频率Tab.1 Pass-band frequency after wavelet decomposition

由于心电信号的QRS波群的频率范围为3～40 Hz，而P、T波的频率范围为0.7～10 Hz，又由于基线漂移的频率小于1 Hz，所以从表1可以得出第8尺度的逼近信号CA8为基线漂移。由于肌电干扰的频率范围为5～2 000 Hz，表1可以得出肌电干扰主要集中在第1、2尺度的细节信号上。由此本文把低频段的基线漂移和高频段的肌电干扰直接置零，把剩下的频段进行心电信号的重构，重构后得到的信号记为f^1（n）：

重构信号如图1所示。

图1 小波分解与重构法的103号心电信号去噪结果Fig.1 Result of the wavelet decomposition and reconstruction denoising No.103 record

为了更清晰地观察和评价小波分解与重构去噪法的去噪效果，图1中的混有噪声的信号为103号记录心电数据上叠加有基线漂移和肌电干扰，文中方法处理的结果如图1最后一个子图，从图可以直观看到小波分解重构法能够很好滤除基线漂移和肌电干扰。

表2 对103号记录去噪效果评价Tab.2 Evaluation of the result of denoising No.103 record

小波去噪性能评价常用标准为信噪比增益（Gain of Signalto-Noise Ratio，简记为 G）、均方根误差（Root-Mean-Square Error， 简称RMSE）和信噪比 （Signal-to-Noise Ratio， 简称SNR）。表2为103号心电数据小波分解重构法去噪后效果的评价。由表2可以得出，小波分解重构法去噪后心电信号的信噪比得到了很好的改善，同时均方根误差有明显的减少。结合表2和图1可得，小波分解重构法可以有效去除心电信号中基线漂移等的噪声。

3 结 论

对MIT-BIT心律失常数据库的心电记录作大量的仿真分析，结果表明小波分解重构法成功的实现了心电信号中的基线漂移和肌电干扰的去除，同时该算法运行速度快，使用比普通的滤波器方便，因为小波分解重构法不需要设计不同截止频率。

小波去噪方法原理简单，处理心电信号时，把干扰信号所在频段直接置零，同时把心电信号的特征波段进行重构，就可以得到去噪后的心电信号。当噪声的频带和信号的频带没有重叠且噪声的频带范围已知时，小波分解重构法有很好的滤波效果。

由于肌电干扰基本覆盖了心电信号的整个频段，所以小波分解重构能够去除大部分的肌电干扰，但是本文采用的算法完好的保留了心电信号的特征波，有用的特征波没有任何的损失。

[1]韦高.基于小波变换的心电信号去噪法[J].中国医学装备，2010，7（8）:9-11.WEI Gao.Denoising algorithm of ECG signals based on wavelet transform[J].China Medical Equipment，2010，7（8）:9-11.

[2]侯宏花，桂志国.基于小波熵的心电信号去噪处理[J].中国生物医学工程学报，2010，29（1）:22-29.HOU Hong-Hua，GUI Zhi-Guo.Denosing Processing of ECG signal Based on Wavelet Entropy[J].Chinese Journal of Biomedical Engineering，2010，29（1）:22-29.

[3]张坤，曹鸣.一种基于小波变换的心电去噪算法[J].现代生物医学进展，2009（9）:3744-3746.ZHANG Kun，GAO Ming.A denoising algorithm of ECG signals based on wavelet transform[J].Progress in Modern Biomedicine，2009（9）:3744-3746.

[4]吕振肃，马文.自适应小波阈值算法在心电信号去噪中的应用[J].数据采集与处理，2009，24（3）:313-317.LU Zhen-su，MA Wen.Application of adaptive wavelet threshold algorithm in ECG signal denoising[J].Journal of Data Acquisition and Processing，2009，24（3）:313-317.

[5]Aydinu，Serinagaoglu D Y.A kalman filter-based approach to reduce the effects of geometric errors and the measurement noise in the inverse ECG problem[J].Medical and Blogical Engineering and Computing，2011（49）:1003-1013.

[6]王晶，那兴宇，谢湘，等.基于多分辨率分析的特征波形分解与重构算法[J].中国科技论文在线，2011，6（7）:519-521.WANG Jing，NA Xing-yu，XIE Xiang，et al.Charac-teristic waveform decomposition and reconstruction algorithm based onmultiresolutionanalysis[J].Sciencepaperonline，2011，6（7）:519-521.

[7]何俊，马有良.心电信号降噪小波函数选取的定量研究[J].信息与电子工程，2010，8（3）：286-289.HE Jun，MA You-liang.Quantitative study on the selection of wavelet functions for the de-noising of ECG signal[J].Information and electronic engineering，2010，8（3）：286-289.