基于无抽样Contourlet变换的图像增强方法
2012-06-09周锦标赵乾宏
李 康,周锦标,赵乾宏
(中国卫星海上测控部 江苏 江阴 214431)
无抽样Contourlet变换不仅具备多尺度、多方向和各向异性特征,还具备平移不变性,因而是一种优良的图像处理工具。文中在无抽样Contourlet变换域构造了一种有效的非线性映射函数,给出了一种基于无抽样Contourlet变换的图像增强方法。实验结果表明,和无抽样小波变换相比,无抽样Contourlet变换可以更好地增强图像的细节信息。
1 无抽样Contourelet变换
Contourlet变换[1]在进行分解和重构过程中,有大量的下采样和上采样操作,使得Contourlet变换缺乏平移不变特性,而变换的平移不变特性在信号处理中发挥着重要的作用。为此,Cunha等Contourlet变换的基础上,提出了无抽样Contourlet变换 (NSCT),它是Contourlet变换的平移不变版本,并且已经应用于图像去噪和图像增强等领域中。
与Contourlet变换类似,NSCT也是将尺度分解与方向滤波分开进行:首先采用无抽样的塔式滤波器(Nonsubsampled Pyramid Filter Bank,NSPFB)获得信号的多尺度分解,然后用无抽样方向滤波器组 (Nonsubsampled Directional Filter Banks,NSDFB)对得到的各尺度子带信号进行方向分解,从而得到不同尺度、方向的子带。与Contourlet变换不同的是,NSCT在信号的分解和重构过程中,取消了下采样和上采样操作,使得NSCT不仅具备多尺度、良好的时频聚集性、高度的方向性和各向异性,而且具有平移不变特性以及各子带之间具有相同尺寸大小等特性。
NSCT采用的NSPFB为二通道无抽样滤波器组,如图1(a)所示。 其中,分解滤波器{H0(z),H1(z)}和合成滤波器{G0(z),G1(z)}满足 Bezout恒等式,如式(1)所示,从而保证了NSPFB满足完全重构(Perfect Reconstruction,PR)条件。与一维“à trous”小波[2]算法相似,NSPFB的每一级滤波器需要对上一级中采用的滤波器按采样矩阵D=2I(其中I为2阶单位矩阵)进行上采样。对于多层NSPFB,j尺度下低通滤波器的理想频率域支撑区间为 [-(π/2j),(π/2j)]×[-(π/2j),(π/2j)],而相应的带通滤波器的理想频率域支撑区间为从频率区间[-(π/2j-1),(π/2j-1)]×[-(π/2j-1),(π/2j-1)]中去除频率支撑区间 [-(π/2j),(π/2j)]×[-(π/2j),(π/2j)]后的部分。因为分解后的低通信号和各尺度下的子带信号与原信号大小尺寸相同,所以NSPFB的冗余度为J+1(J为NSPFB分解的级数)。

NSCT采用的NSDFB也是一组二通道非下采样滤波器组,如图 1(b)所示。 其中,分解滤波器{U0(z),U1(z)}和合成滤波器{V0(z),V1(z)}也满足 Bezout恒等式,如式(2)所示,从而也保证了NSDFB满足完全重构条件。采用理想频率支撑区间为扇形的滤波器U0(z)和U1(z)可以实现二通道方向分解。在此基础上,对滤波器 U0(z)和 U1(z)采用不同的采样矩阵进行上采样,并对上一级方向分解后的子带信号进行滤波,可以实现频域中更为精细的方向分解。例如,可以对滤波器U0(z)和 U1(z)分别按采样矩阵进行上采样得到滤波器 U0(zQ)和 U1(zQ),然后再对第一级二通道方向分解后得到的子带进行滤波,可以实现四通道方向分解。对于更多方向的分解,需要采用更为复杂的采样矩阵对滤波器进行上采样。如果对某尺度下的子带进行1级方向分解,可得到21个与源信号尺寸大小相同的方向子带。
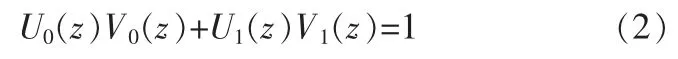

图1 NSCT中的二通道无抽样滤波器组Fig.1 Nonsubsampled filter banks in NSCT
将NSPFB与NSDFB相结合,就可以实现NSCT。源信号经NSPFB分解后得到的高频带通信号再输入到NSDFB中以获得带通方向子带,该过程在NSPFB输出的近似分量上迭代进行,从而实现对源信号的多尺度、多方向分解。由NSPFB和NSDFB的冗余特性,可以得到NSCT的冗余度为,其中J为分解尺度数,lj为j尺度下的NSDFB分解级数。
2 图像增强方法描述
基于多尺度变换的细节信息增强方法的基本思想是用映射函数来修改原始信号的变换系数,然后用修改后的变换系数进行重构[3-5]。为了有效抑制噪声系数、增强细节信息系数,通常使用的是非线性映射函数且该函数应具备以下条件[6]:1)强边缘不应变模糊;2)细节信息应当比强边缘得到更高的增强;3)具有单调性;4)具有反对称性。我们在NSCT域构造了一种简单而有效的非线性映射函数:

其中,角标 j、k 和(m,n)分别代表尺度、方向和位置;C(j,k,m,n)表示 原 始 信 号 的 NSCT 系数 ,C^(j,k,m,n)表示 修 改 后 的 NSCT 系数;M(j,k)表示子带内系数幅值的最大值;T(j,k)是门限阈值,用于抑制随机噪声,这里我们选用K-sigma阈值;p是一个常数,用于控制映射函数的形状和增强的程度,图2给出了p值不同时,修改后的NSCT系数和原始信号的NSCT系数之间的关系。可以看到:为了增强细节信息,参数p应当满足0<p≤1;而且增强的程度随着参数p的减小而增大。在增强区间[T(j,k),M(j,k)]和[-M(j,k),-T(j,k)]内,映射函数的斜率大小随 着系数幅值 的增大而减小,从而,和强边缘相比,对应于较小幅值系数的细节信息会得到更大的增强;小于和略大于门限 T(j,k)的小幅值系数对应于噪声和扰动,这些系数可被有效地抑制;此外,该非线性映射函数显然满足单调性和反对称性。
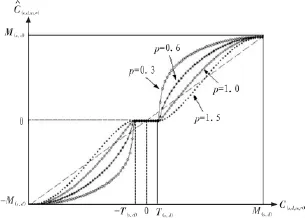
图2 修改后NSCT系数和原始系数之间的关系Fig.2 Enhanced coefficients versus original coefficients
基于无抽样Contourlet变换的细节信息增强的方法可总结如下:
1)对输入的二维信号进行NSCT变换,从而得到NSCT系数。
2)用式(3)的非线性映射函数修改系数 C(j,k,m,n),从而得到修改后的系数C^(j,k,m,n)。
3)用C^(j,k,m,n)进行 NSCT 重构,得到增强后的信号。
3 实验结果
我们选择 512×512大 小 的标准 图 像 Barbara、Lena、Peppers进行实验,采用3尺度NSPFB变换,从最细尺度到最粗尺度,每个尺度下的方向数目依次取8、4、4,取0.7。表给出了使用不同方法降噪后图像的细节方差 (DV)和背景方差(BV),可以看到,基于无抽样Contourlet变换的图像增强方法可以更好地增强图像的微弱信息。

表1 不同增强方法的增强效果比较Tab.1 Enhancement results with different m ethod
4 结 论
文中研究了基于无抽样Contourlet变换的图像增强方法,在无抽样Contourlet变换域构造了一种简单有效的非线性映射函数,利用无抽样Contourlet变换的多尺度、高度方向性和各向异性以及平移不变特性实现图像细节的增强,并用测试图像算例验证了该方法的优越性。
[1]Do M N,Vetterli M.The contourlet transform:an efficient directional multiresolution image representation[J].IEEE Transactions on Image Processing,2005,14(12):2091-2106.
[2]Mallat S.A wavelet tour of sinal processing[M].2nd ed.New York:Academic,1999.
[3]Lu J,Jr.Healy D M.Contrast enhancement of medical images using multiscale edge representation[J].Optical Engineering,1994,33(7):2151-2161.
[4]Laine A,Fan J,Yang W.Wavelets for contrast enhancement of digital mammography[J].IEEE Engineering in Medicine and Biology Magazine,1995,11(5):536-551.
[5]ZONG Xu-li, Andrew F L, Edward A G, et al.De-noising and contrast enhancement via wavelet shrinkage and nonlinear adaptive gain[J].Wavelet Applications,Proceedings of SPIE,1996,2762:566-574.
[6]Sakellaropoulos P,Costaridou L,Panayiotakis G.A waveletbased spatially adaptive method for mammographic contrast enhancement[J].Physics in Medicine and Biology,2003,48(6):787-803.
