模糊参数自适应自整定的逆变电源系统研究
2012-06-09金平,尚凯
金 平, 尚 凯
(1.中国商用飞机上海飞机设计研究院 上海 200232;
2.西北工业大学 无人机特种技术重点实验室,陕西 西安 710065)
随着正弦波脉宽调制(SPWM)逆变技术的日益成熟,逆变电源被广泛应用到微波通讯、野外活动、高速公路、海岛、军事、医疗、航空航天等各个领域。逆变电源的负载可能具有不同的性质,如阻性负载、感性负载和整流型负载等,当某一负载投入运行时,特别是非线性负载,很可能引起逆变器的输出电压波形周期性畸变,谐波增加。谐波对供电系统的污染日益严重,它对各种电气设备都有不同程度的影响和危害[1]。因此逆变电源需要向各种负载提供高质量的电能,也就显示出了逆变器输出波形控制的重要性。
逆变电源的控制有多种方案,如闭环控制[2],重复控制[3],无差派控制[4]和模糊控制[5]等。其中模糊控制器以其不需要被控对象的精确数学模型,较强的鲁棒性和自适应能力,查找模糊控制表只需要占用处理器很少的时间等优点,因而可以采用较高采样率来补偿模糊控制规则和实际经验的偏差。文中正是基于模糊控制的原理提出了一套逆变电源的自适应自整定控制方法,并通过SIMULINK仿真实现了逆变电源电路模型的建立、模糊推理运算、自整定和自适应的功能,利用powergui模块测量了总谐波含量,验证了该方法的可行性和优越性。
1 逆变电源自适应自整定控制系统模型
模糊自适应自整定控制器结合了自适应和自整定的功能,所以该新型控制器的模糊参数自整定控制器用来在线整定Kp的大小,模糊参数自适应控制器用来在线自适应比例因子的大小[6]。基于这些分析,文中设计了该新型控制器的原理框图,如图1所示。
MATLAB作为一种开放的编程语言,提供了多种用户扩展工具,相继推出的建模可视化功能SIMULINK和工具箱为控制系统仿真和设计提供了有力的工具。MATLAB为电力系统仿真设计了电力系统模块集,用其中的元件可以方便搭建较为精确的逆变控制系统的仿真模型。
自整定控制器整定Kp,自适应控制器对于自整定控制器的比例因子进行在线调整。误差e和它的导数ec作为这两个二维模糊控制器的输入,经过设置好相应的模糊规则推理后进行输出。自整定控制器输出结果和自适应控制器输出结果相乘后作为反馈结果信号。这样就实现了对于逆变电源Kp参数的在线模糊自整定自适应控制。
2 模糊控制器参数的设置
在系统控制过程中,比例因子对系统控制性能和稳定性影响最为明显,尤其表现在系统初始运行阶段。从手动控制经验看也是如此,操作者主要是根据误差和误差变化,以及系统的控制性能指标来调整控制器的输出增益,即比例因子的大小,以达到理想的控制效果。比例因子自整定模糊控制器就是基于这种思路而产生的。
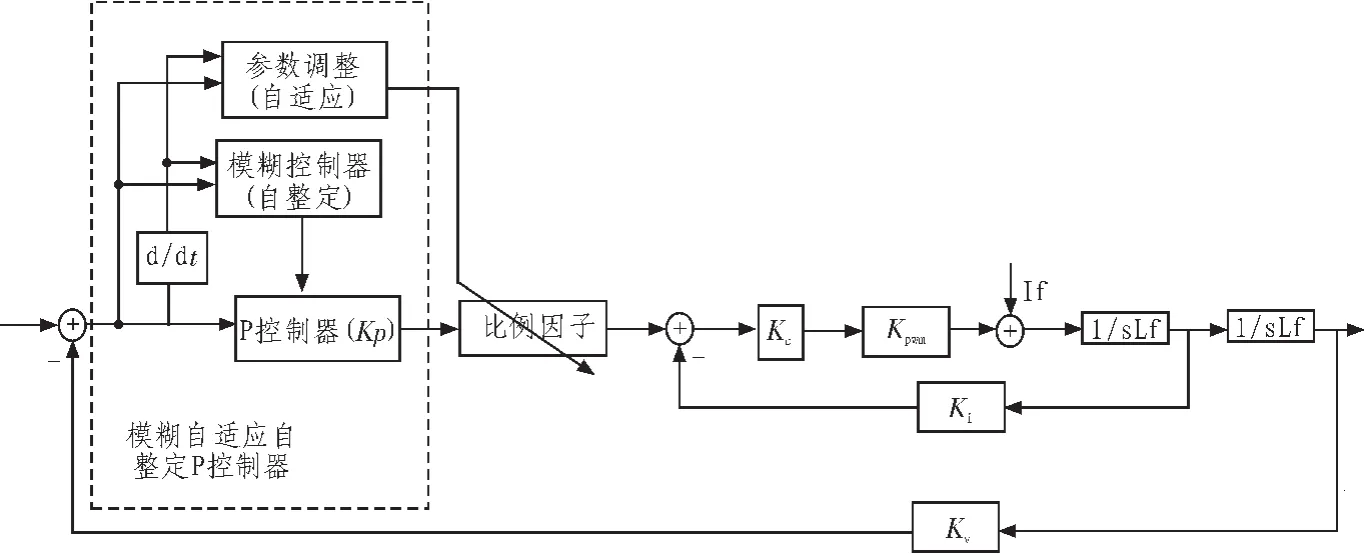
图1 模糊自适应自整定控制器原理框图Fig.1 Adaptive fuzzy self-tuning controller block diagram
所采用的自整定模块控制器和自适应模块控制器的输入输出隶属度函数均采用七段标准高斯分布函数,模糊规则排列方式也相同,差别仅在于分布区间不同。以自整定控制器模糊规则图为例说明所有模糊控制器参数的设置,如图2所示。

图2 自整定控制器模糊规则图(输入和输出)Fig.2 Self-tuning controller fuzzy rules(Input and Output)
自整定控制器的输入输出规则和区间分布均相同,按照{NB,NM,NS,ZO,PS,PM,PB}顺序排列。自适应控制器模糊规则图的输入区间为[-1,1],输出区间为[0.5,1.5],排列方式和与图2所示相同。
3 仿真实验及波形结果
仿真实验是通过MATLAB/SIMULINK进行的。其中幅值较大的为仿真电压波形,幅值较小的为仿真电流波形。通过FFT analysis可以直观的看到对应仿真波形的总谐波失真(Total Harmonic Distortion, THD)。
3.1 阻性负载 R=10Ω
此处实现的逆变电源[7]系统性能为输入单相交流电压220 V,频率50 Hz;输出交流电压115 V(有效值115 V,峰值163 V),频率400 Hz。在图3所示的输出波形图中,幅值高的为输出电压波形,幅值低的为输出电流波形。由图可得,自适应自整定控制器阻性负载启动调节时间仅为2个周期左右,而且几乎无超调;图4所示的阻性负载输出电压的THD值仅为0.34%,远小于一般的要求。阻性负载的突减/突加负载波形十分完美,因篇幅所限,阻性负载突减/突加负载波形图略去。
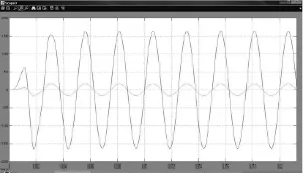
图3 带载启动电压波形图Fig.3 Load to start the voltage waveforms

图4 阻性负载输出电压THD值Fig.4 Resistive load output voltage THD value
3.2 非线性负载(整流桥负载)
将整流桥负载加至逆变器输出端,并进行仿真实验。由SIMULINK仿真结果可看出,自适应自整定控制器带整流桥负载启动时间仅为2个周期左右如图5所示,几乎无超调;非线性负载输出电压的THD值仅为0.38%,远小于一般的要求如图6所示。

图5 整流桥负载启动电压波形Fig.5 Bridge rectifier load to start the voltage waveform
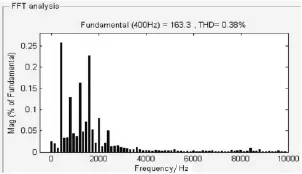
图6 整流桥负载输出电压THD值Fig.6 Bridge rectifier load output voltage THD value
由图7所示的突减整流桥负载和图8所示的突加整流桥负载可看出,该新型控制器对于突变整流桥负载具有十分优越的波形。从(图3~图8)仿真图形结果可以看出,无论是线性负载还是非线性负载,无论是启动波形还是突变负载波形,该新型自适应自整定控制器超调量小,调节时间短,突加突减负载输出电压波形几乎不变化,性能十分优越。
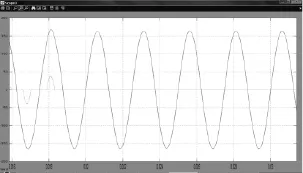
图7 整流桥突减负载电压波形Fig.7 Rectifier bridge suddenly reduce the load voltage waveform

图8 整流桥突加负载电压波形Fig.8 Rectifier bridge suddenly increase the load voltage waveform
4 结 论
文中针对逆变电源系统提出了一种全新的模糊参数自整定自适应控制系统。从仿真结果可以看出,这种新的控制方法的引入,既可以实时修改系统的Kp,又可以修改比例因子,从两方面同时使系统获得十分优良的动态性能。其快速的响应速度和较强的鲁棒性说明这种自整定自适应模糊控制是一种具有实用价值的控制方案,完全能够逆变电源苛刻的精度要求,对相关工程技术人员有很好地参考价值。
[1]刘凤君.正弦波逆变器[M].北京:科学出版社,2002.
[2]Kawamura A,Yokoyama T.Comparison of five different approaches for real time digital feedback control of PWM inverter[J].IEEE IAS,1990:1005-1011.
[3]李翠艳,张东纯,庄硅义.重复控制综述[J].电机与控制学报,2005,9(1):37-44.LI Cui-yan,ZHANG Dong-chun,ZHUANG Gui-yi.Repetitive control-a survey[J].Electric Machines and Control,2005,9(1):37-44.
[4]郭卫农,段善旭,康勇,等.电压型逆变器的无差拍控制技术研究[J].华中理工大学学报,2000,28(6):30-33 GUO Wei-nong,DUAN Shan-xu,KANG Yong,et al.The deadbeat control of PWM VSI[J].Journal of Huazhong University of Science and Technology,2000,28(6):30-33.
[5]李士勇,模糊控制.神经控制和智能控制[M].哈尔滨:哈尔滨工业大学出版社,1998.
[6]马长华,朱伟兴.比例因子对模糊控制器动态性能的影响[J].江苏理工大学学报:自然科学版,2000,21(5):87-90.MA Chang-hua,ZHU Wei-xing.Scale factor on the dynamic performance of the fuzzy controller[J].Journal of Jiangsu University of Science and Technology,2000,21(5):87-90.
[7]刘辉,韩如成,智泽英.基于同伦算法的逆变电源特定消谐法的研究[J].现代电子技术,2009(8):173-177.LIU Hui,HAN Ru-cheng,ZHI Ze-ying.Homotopy-based Research on Harmonic Elimination Model in PWM Inverter[J].Modern Electronics Technique,2009(8):173-177.
