结构化与非结构化网格融合技术研究
2012-06-08项立银
项立银,陈 杨
(中国船舶重工集团公司第七二四研究所,南京 210003)
0 引言
网格划分是有限元计算的基础,高质量的网格对有限元计算的结果至关重要。数值计算中采用的网格通常可以分为两类,结构化网格与非结构化网格[1]。结构化网格是指网格区域内的节点都具有相同数目的毗邻单元,具有所需单元数量少、计算速度快、计算精度高等优点,但适应性差,适用于形状规则的几何体;非结构化网格是指网格区域内的内部点不具有相同的毗邻单元,即与网格剖分区域内的不同内点相连的网格数目不同。非结构化网格消除了结构网格中节点的结构性限制,节点和单元的分布可控性好,因而能较好地处理边界。适用于模拟真实复杂外型,但收敛特性较差,计算精度低。
为了兼顾有限元计算对精度和效率的要求,本文将结构化与非结构化网格划分技术融合起来。对于大型的三维模型,其相对规则部分用结构化网格划分,不规则部分用非结构化网格划分。通过网格拓扑转化技术将交界面处的四面体网格转化成三角形网格来满足拓扑一致,实现网格连接,生成高质量的有限元计算网格。
1 方法原理
工程或物理学中的许多问题通常是以未知函数应满足的微分方程和边界条件的形式提出来的,可以一般地表示为未知函数u 应满足微分方程组[2-3]:

同时,未知函数u 还应满足边界条件:
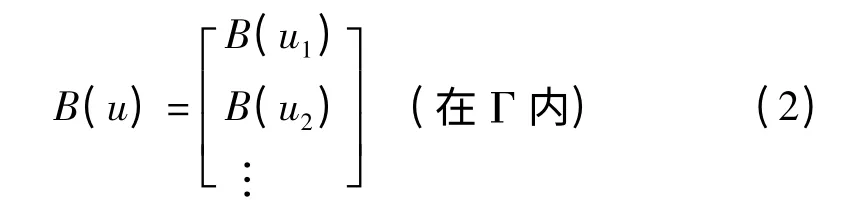
其中,Ω为域,Γ为域Ω的边界。
假如边界条件(2)同时满足边界上的每一点,则等效积分方程

在求解域Ω中,若场函数u 是精确解,则在域Ω中任一点都满足微分方程(1),同时在边界Γ 上任一点都满足边界条件(2),此时等效积分形式(3)必然得到严格满足。但是,对于复杂的实际问题,这样的精确解往往是很难找到的,因此需要找到具有一定精度的近似解。
假设u 可以采用近似函数来表示,一般形式为
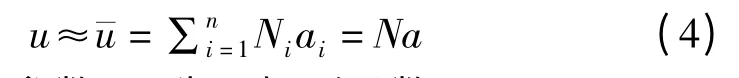
其中,ai是待定参数,Ni为已知形函数。
对于三维力学问题,可取近似解:

显然,在通常n 取有限项数的情况下近似解是不能精确满足(1)和(2)的,形函数Ni的项数n 越多,近似解的精度将越高。对于三维力学问题,四面体的形函数n=4,六面体的形函数n=6,显然在相同条件下六面体的计算精度要高于四面体。
有限元计算的精度和效率一直是一对矛盾体。采用非结构化网格可以自动化分,但计算精度低,有时为了得到较精确结果而细化网格,计算量又太大甚至导致现有计算机无法计算。采用结构化网格计算精度高,但现有软件通常不能自动划分,需要用户手动参与,对几何体进行分割等操作[4]。对于一些特别复杂的模型,即便人工参与划分网格,要将三维模型切割成几十甚至上百块,结构化网格难以实现。
为了取长补短,充分利用结构化网格和非结构化网格的各自优势,在网格划分的时候把几何拓扑相对规则的部分化成六面体网格,而把相对复杂的部分化成四面体网格,但六面体网格无法向四面体网格自由过渡。本文采用网格拓扑转换实现网格连接,将六面体网格的交界面四边形网格转化成三角形网格来满足连接拓扑一致,通过将转化而来的三角形网格作为网格边界实现连接面的节点匹配,最终生成期望的高质量网格。
2 算例
2.1 网格划分方法
以一简单例子说明本文的网格划分方法。如图1所示,将模型分为两个区域(六面体网格区域和四面体网格区域),首先进行六面体网格区域的网格划分,并将图示交界面区域的四边形网格转化成三角形网格,以转化的三角形网格作为四面体网格划分的边界条件,进行四面体网格划分[5]。从最终的网格模型可以看出,在交界处这两类的网格匹配得相当好。

图1 网格划分方法示意
2.2 模型介绍
为了验证上述方法的可行性与有效性,选取某通用机柜对其进行模态分析。如图2所示,该机柜总体尺寸较大,高度达到了1510 mm,而两侧壁较薄,仅为4 mm。但两侧壁几何相对规则,而顶部和底部几何形状复杂,小特征较多。

图2 通用机柜三维模型
2.3 有限元模型
分析机柜的结构特点可以看出,机柜主体中间两侧壁部分形状较为规则,顶部和底部几何形状复杂。若全部采用非结构化四面体网格划分,能较好地处理顶部和底部复杂的边界,但单元数较多,达到了47204个单元,15778个节点;若全部采用结构化六面体网格划分,单元数较少,两侧壁较容易实现但顶部和底部几何过于复杂,难以实现。因此,本文提出结构化与非结构化相融合的网格对其进行网格剖分。首先,对两侧壁进行六面体网格划分,并将交界面区域的四边形网格转化成三角形网格,以转化的三角形网格作为顶部和底部网格划分的边界条件,进行四面体网格划分。图3左侧为纯四面体网格模型,右侧为融合网格模型,共划分了28037个单元,18086个节点。

图3 机柜两种网格划分对比
2.4 仿真结果
仿真计算的约束条件与试验安装状态一致,约束机柜底部3个方向的平动自由度与转动自由度,对四面体网格模型和融合网格模型进行模态分析,四面体网格模型的一阶模态为37.13 Hz,振型如图4所示。融合网格模型的一阶模态为24.87 Hz,振型如图5所示。

图4 四面体网格机柜一阶模态振型

图5 融合网格机柜一阶模态振型
2.5 仿真与实验结果对比
在振动试验平台上固定机柜底部对该机柜进行振动实验。由于该实验平台测量范围的限制,故只采集了一阶模态,为28 Hz,结果见图6。四面体网格模型和融合网格模型一阶模态仿真结果与实验结果对比见表1。

图6 机柜一阶模态试验结果

表1 机柜一阶模态仿真与实验结果对比
从结果中可以看出,两种网格划分的机柜的一阶模态振型一致,与实验结果都存在一定的偏差,但四面体网格的结果误差较大且偏大,这是由于四面体网格偏刚性所致;混合网格的结果误差较小,与实验结果吻合较好。
3 结束语
本文中所述结构化与非结构化相结合的融合网格,所需单元数量少、计算速度快,采用网格拓扑转换实现网格连接,适用于形状不规则的几何体,与实验结果对比发现计算精度较高,完全满足工程仿真的需求。
[1]李扬,唐巨山,张婷.拓扑映射法划分结构化六面体网格在水利工程方面的应用[J].水利与建筑工程学报,2011,9(3):134-137.
[2]王勖成.有限单元法[M].北京:清华大学出版社,2003:14-20.
[3]朱伯芳.有限单元法原理与应用(第3 版)[M].北京:中国水利水电出版社,2009:127-128.
[4]刘声,盛选禹.基于结构化网格自动划分的汽车发动机强度分析[J].计算机工程与设计,2010,31(10):2316-2319.
[5]向华平.基于边界拓扑转化的四面体与六面体网格动态连接技术[J].安徽大学学报,2011,35(2):43-46.
