深水钢悬链线立管顺流向非线性动力分析

孟 丹，郭海燕

（中国海洋大学 工程学院，山东 青岛 266100）

1 引 言

随着开采水深的增加，近年来发展起来的新型立管系统—钢悬链线立管（Steel Catenary Riser）—在技术上和经济上比传统的柔性立管和顶张力立管系统有了长足的进步，成为深海油气资源开发的首选立管形式。1994年安装了世界上第一条钢悬链线立管，引起了工程界和学术界的极大关注[1-5]。钢悬链线立管作为输送油气资源的管道连接于海底和上部浮体之间，在波浪和流的作用下，不仅上部浮体产生的复杂动力响应会作用于深水海洋立管[6]，立管本身也承受着强度相当大的波浪和流的作用力。准确地预报出实际海况中钢悬链线立管的动力响应问题，对于逐渐向深海发展的海洋开采事业具有重大的意义[7]。

以往对深水海洋立管这种细长的柔性结构多采用大位移小应变的分析方法，而实际上即使对于伸展性不明显的立管结构，大应变的影响都不可忽视[8]。而且在以往的分析中，都是将外部流体的非线性作用力进行线性化，甚至忽略流体阻尼的影响，不能反映外部流体对立管振动的实际影响。因此，本文考虑深水钢悬链线立管大应变的特性以及内流的影响，采用具有弯曲刚度的细长梁模型模拟钢悬链线立管，利用Hamilton原理和拉格朗日应变理论建立了立管的二维动力学模型。通过Hermite插值函数对动力学方程进行有限元离散。由于系统的多重非线性，系统方程的求解采用时域的逐步积分法，积分格式选用Newmark-β法。探讨了在外部流体非线性作用力的影响下立管的动力响应。

图1 深水钢悬链线立管大变形示意图Fig.1 Schematics of large deformations of deepwater steel catenary riser

2 动力学模型的建立

图1给出了典型的上部连接于浮体的自由悬挂钢悬链线立管的构型图，水深为xH，顶部的静止偏移为yV。立管顶端作用有初始的拉力Tt以保持立管的初始构型。立管上每一点的坐标都通过笛卡尔坐标系确定。图中定义了立管的三种状态分别为初始态、平衡态以及动态。立管在初始状态下，由于其自重、内流的作用、轴向和弯曲变形达到平衡状态。同时，平衡状态被认为是立管动力学计算的初始状态。在外部荷载的作用下，立管会由平衡态发展到动态，u1、u2和 u3分别为立管微元 ds0从平衡态到动态在X、Y和Z方向上的位移。在本文的研究中，只考虑立管在XOY平面内的运动，即 u3=0。

在立管的平衡状态微元ds0的长度为

利用拉格朗日应变理论，在立管的初始态和动态微元的长度分别为：

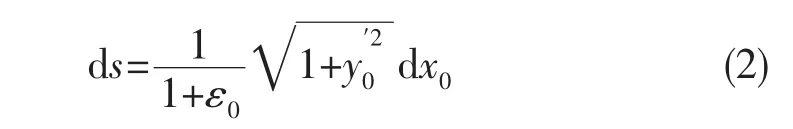
其中ε0为初始的静应变，则动态立管的总应变为

2.1 能量方法

立管轴向应变能Ua由两部分组成，一部分由轴向力引起，一部分由流体静压力组成：

其中，ST为未变形前立管的总长度，A为动态时立管的横截面积；初始应力σov=2νσp，ν为泊松比，端部应力[9]σp=（peAoe-piAoi）/Ao，pe、pi分别为立管外部和内部流体对管壁的静压力，Ao为平衡位置立管的横截面积。

轴向应变能的变分表达式为

并且 Ta=EA0ε0+σ0vA0，Tb=EA0-σ0vA0。 且仅当泊松比 ν=0.5 时，Ta=EA0ε0+σpA0即为有效拉力。 忽略高阶项并应用二项式近似有

应用（8），（9）式，方程（6）可简化为

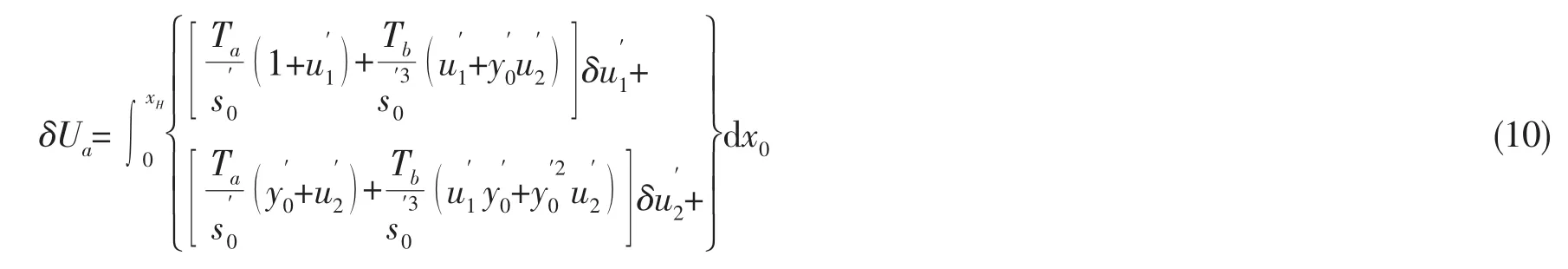
根据Euler-Bernoulli梁理论，忽略剪切变形的影响，在XOY平面内非线性应变曲率和位移的关系可表示为

其中κ*和κ分别为动态和平衡状态时管道的曲率。

弯曲应变能Ub为

其变分表达式为

因此，立管应变能的变分为

进行立管的动力分析，外力所做的虚功包括有效重力、外部流体以及惯性力所做的虚功[8]，其中由有效重力做的虚功可表示为：

其中

并且ρ为初始位置单位长度管道质量，ρf为平衡初始位置单位长度内部流体质量，ρe为外部流体密度，g为重力加速度。

由外部流体做的虚功δWH可表示为：

其中pn为外部流体作用在立管上的正压力，根据Morison方程有

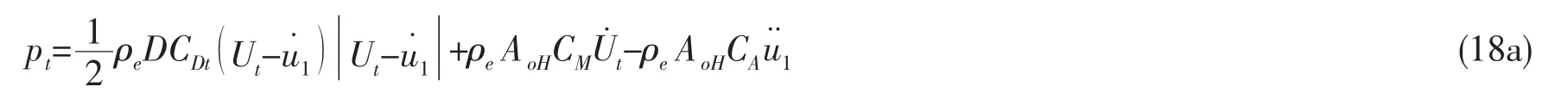
pt为外部流体作用在立管上的切向力

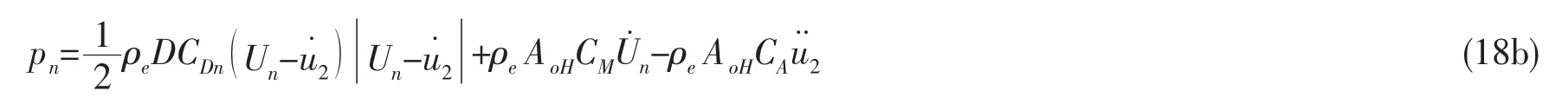
并且CDn、CDt分别为法向、切向拖曳力系数；D为管道外径；Un、Ut分别为外部流体在法向、切向上的流速；CM为惯性系数；CA为附加质量系数。

根据牛顿第二定律，惯性力可表示为

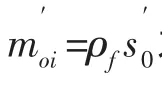
其中V为立管内部流体的流速。因此，外力所做的虚功为

2.2 运动方程

根据虚位移原理

可以得到动力学系统在虚位移δu1和δu2上的Euler’s方程，将立管在平衡位置的初始条件代入Euler’s方程可得系统在平衡位置处的静力平衡方程。由于平衡位置是系统进行动力分析的初始状态，所以联合静力平衡方程和Euler’s方程便可得到系统的运动方程：

3 求解方法及模型验证

将运动方程（23）写成矩阵的形式为

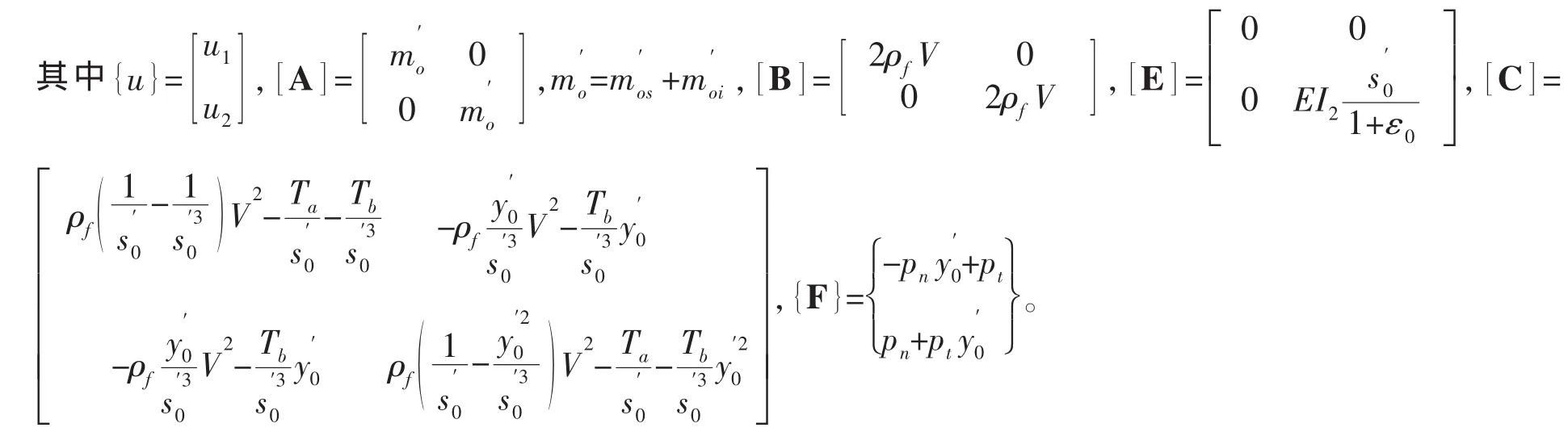
将水深xH分成n个长度为l的单元，则相对应的立管单元内任意一点的位移可表示为

根据Galerkin有限元法，运动方程变为

为了得到立管的动力响应，利用数值积分的方法，即Newmak-β法和Newton-Raphson迭代法对动力学方程进行求解。Newmak-β法积分参数取值为

立管的边界条件为

立管动力响应的初始条件为

用MATLAB将上述算法编写程序resp.m，用于计算海洋立管在外部流体以及内流影响下的动力响应。

为了验证本文建立的模型的正确性，选取参考文献[11]中的数据进行计算，参考文献中的深水立管的物理参数列于表1中。首先计算立管的自然频率，计算结果以及与参考文献的比较结果列于表2，从计算结果可以看出，本文模型的基频大小与以往计算结果非常接近；其次，图2中给出了本文编制的计算程序resp.m和参考文献[12]立管中点动力响应计算结果，从图中可以看出，两种方法的计算结果基本一致。

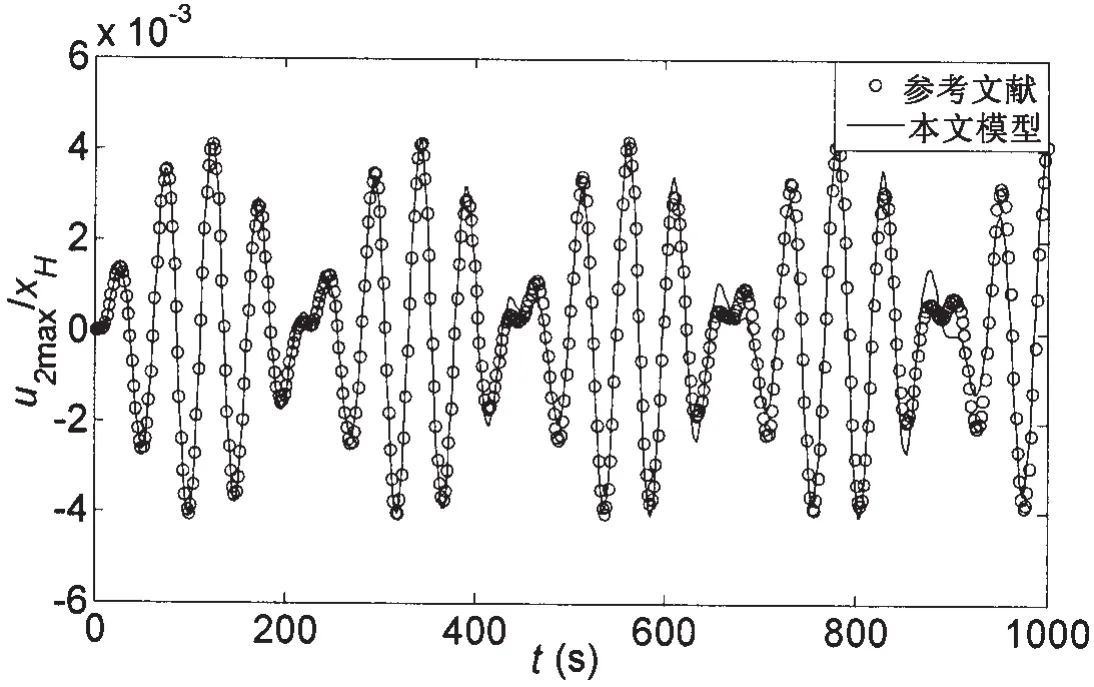
图2 海洋立管中点动力响应时程曲线Fig.2 A comparison of displacement responses in the middle of the riser

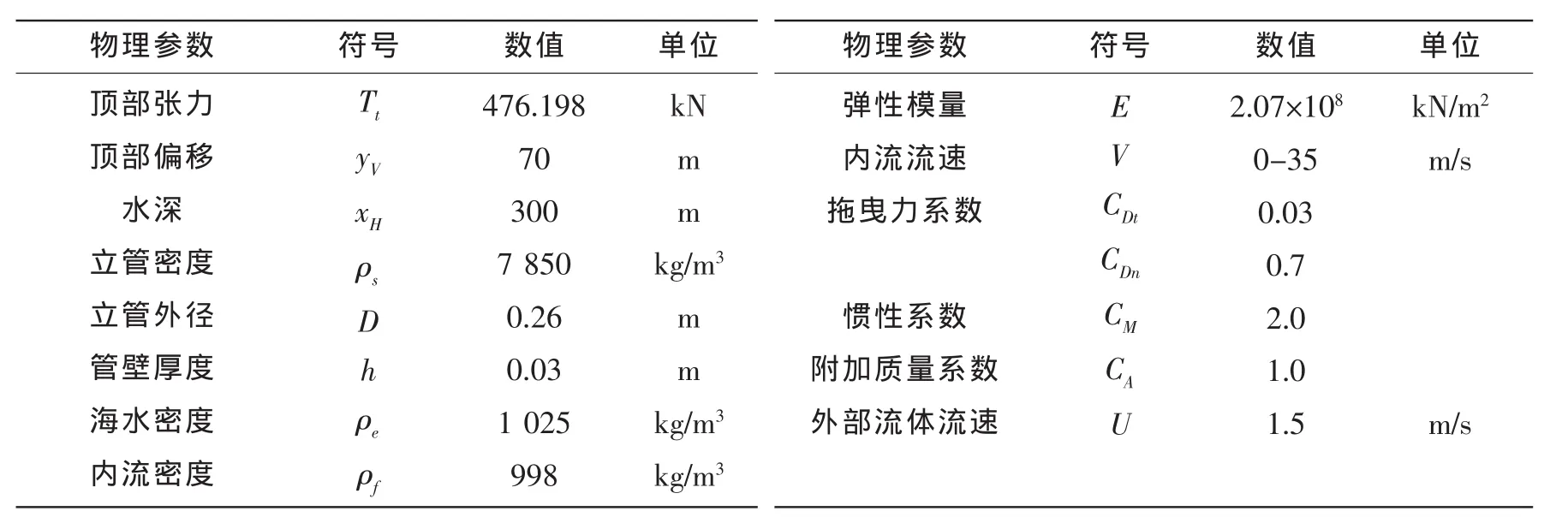
表1 深水海洋立管的物理参数Tab.1 General material properties of marine risers

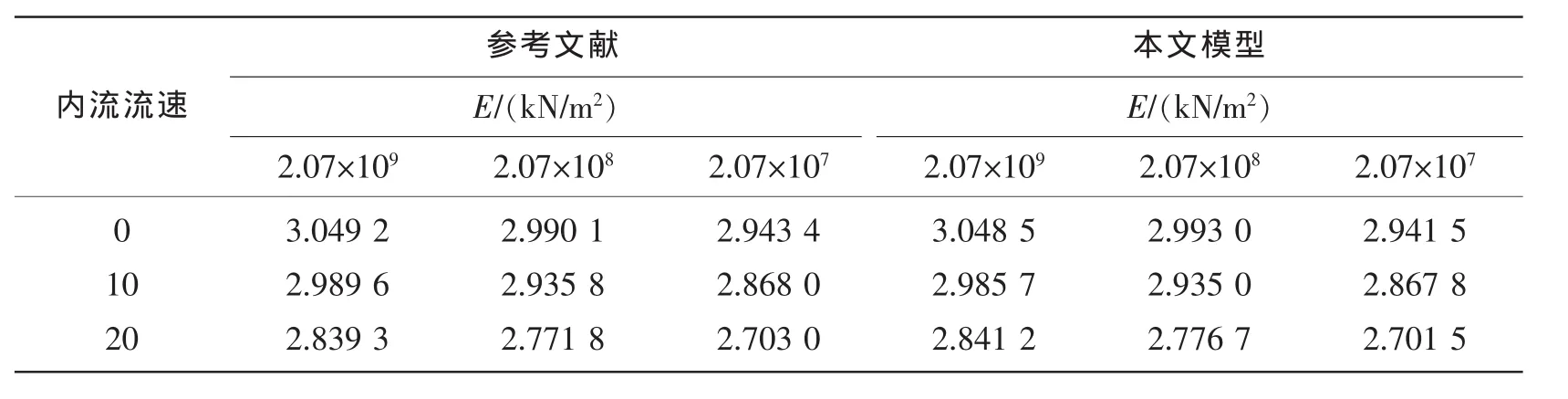
表2 基频比较结果Tab.2 Comparison of fundamental frequencies

4 结果与讨论

在外部流体影响的参数分析中，假设外部流体为稳定流，流速沿Y轴正向流动，且速度为U。为了考虑外部流体非线性的影响，定义符号函数

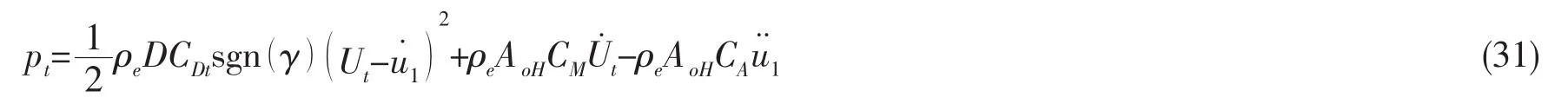
方程（18b）同理，将其代入（26）式计算外部流体的作用力。

为了研究立管的动力响应，我们假设立管顶部受到大小为0.1 kN、频率为ωs的正弦激励，并定义频率比fr=ωs/ωf，并且变化范围取为0.5-2.0，其中ωf为立管的自振频率。

4.1 激励频率对动力响应的影响

在外部流体作用下不同激励频率时，立管的位移响应曲线在图3中给出。从图中可以看出，立管的动力响应具有明显的非线性，而且外部流体的存在减小了立管的动力响应幅值。随着激励频率的增大，动力响应的最大位移也变大，直到fr=1.0时，立管发生共振现象。继续增加激励频率值，立管的响应最大位移减小。

其中 γ=U-u˙2。 则方程（18a）变为

4.2 外部流体流速对共振响应的影响

图4给出了不同外流流速情况下的深水海洋立管共振响应曲线。从图中的结果可以看出，随着流速的增加，管道的共振响应会趋于稳定状态，响应幅值变小，趋于稳定的时间也变小。不同外部流体流速时管道振动趋于稳定所需的时间及响应幅值见表3。

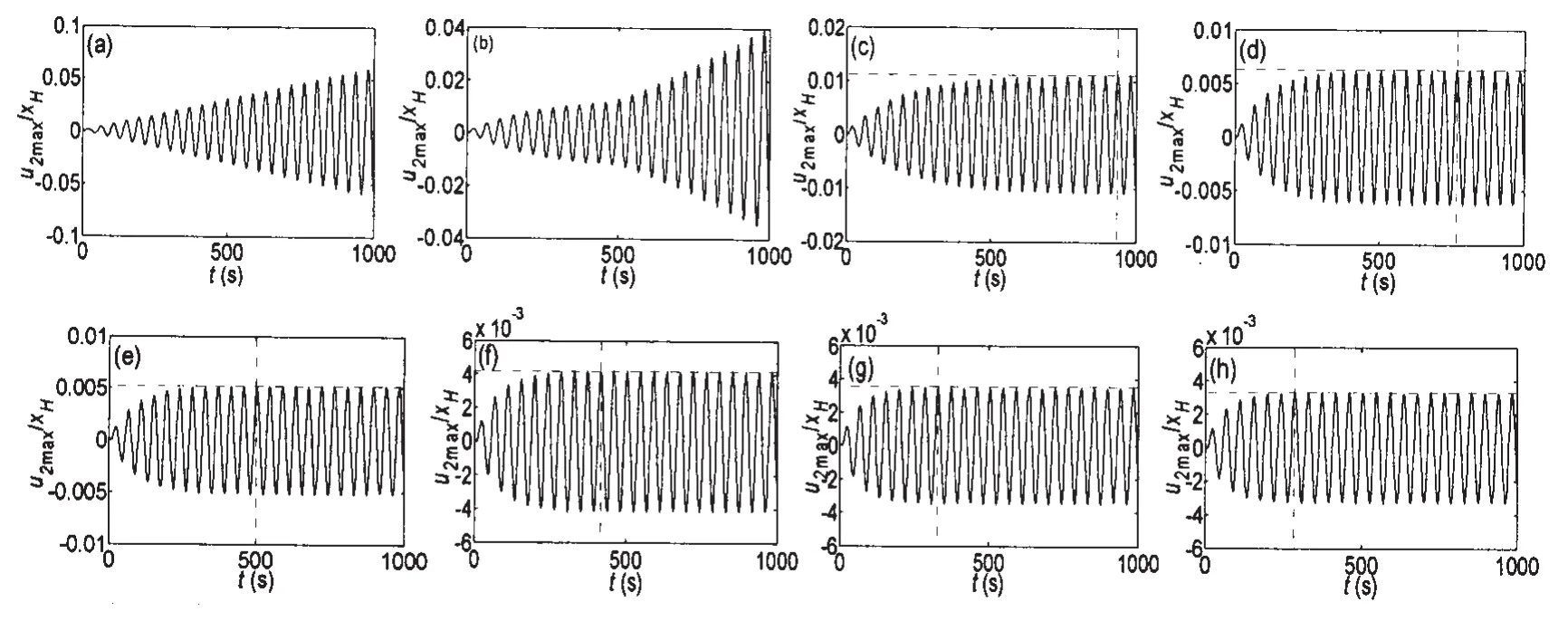
图 4 海洋立管共振响应曲线：（a） U=0；（b） U=0.5；（c） U=0.6；（d）U=1.0；（e） U=1.2；（f） U=1.5；（g） U=1.8；（h） U=2.0Fig.4 Resonant responses of marine risers:(a)U=0;(b)U=0.5;(c)U=0.6;(d)U=1.0;(e)U=1.2;(f)U=1.5;(g)U=1.8;(h)U=2.0

4.3 拖曳力系数对共振响应的影响

自Morison方程提出几十年来，已有不少学者对CD进行了大量的模型试验和现场观测工作，但所得数据仍有相当大的离散性。拖曳力系数反映了管道表面的粗糙程度，和雷诺数的大小有关系。本文根据1976年Sarpkaya的实验数据，假定CD的大小在0到2.0范围内。U=0.75 m/s时海洋立管第一阶模态的共振响应曲线在图5中给出。从图中可以看出，拖曳力系数的大小直接影响海洋立管动力响应幅值的大小。由于拖曳力的存在，在开始振动一段时间后，管道的动力响应趋向于一个稳定状态。并且，拖曳力系数的值越大，动力响应的稳定幅值就越小，具体变化见图6。

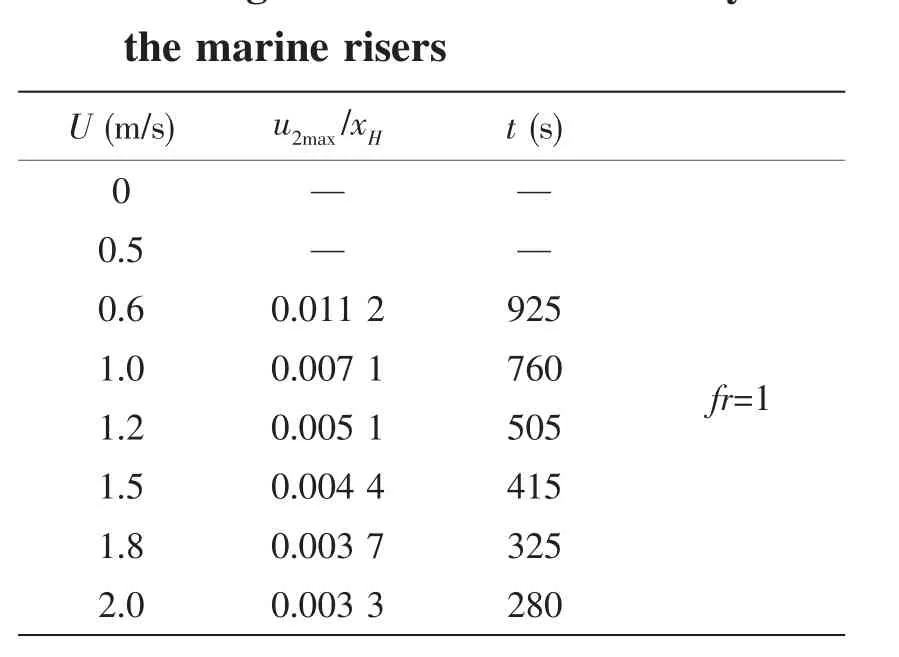
表3 海洋立管动力响应稳定时间Tab.3 Convergence time onto the steady state of

图 5 海洋立管共振响应曲线：（a） CD=0；（b） CD=0.4；（c） CD=0.8；（d）CD=1.2；（e） CD=1.6；（f） CD=2.0Fig.5 Resonant responses of risers:(a)CD=0;(b)CD=0.4;(c)CD=0.8;(d)CD=1.2;(e)CD=1.6;(f)CD=2.0

5 结 论

本文研究了深水钢悬链线立管在外部流体作用下的动力响应。基于能量方法，立管的应变能主要由立管伸长和弯曲产生，外力所做虚功则来源于立管的重力、立管和内流产生的惯性力、以及外部流体的作用，建立了深水输流立管大应变动力学模型。有别于以往的研究，模型的非线性充分体现在大位移大应变理论的应用。从管道的动力响应分析中发现了共振现象，并且，外部流体的非线性作用会影响立管位移响应的幅值以及位移响应趋于稳定的持续时间。

拖曳力系数取值不同，立管的动力响应幅值也不同。在深水海洋立管的设计中，应针对不同的外部海洋环境，通过实验确定拖曳力系数。

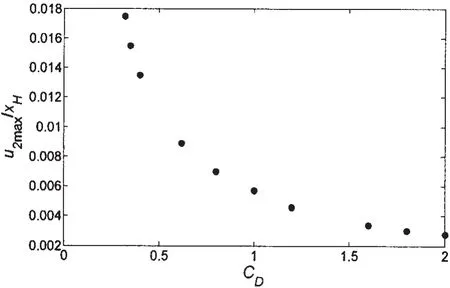
图6 海洋立管共振响应幅值与拖曳力系数关系曲线Fig.6 Relation between maximum dynamic responses of risers and drag force coefficients

[1]Egil Giertsen,Richard Verley,Knut Schroder.CARISIMA a catenary riser/soil interaction model for global riser analysis[C]//Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering-OMAE.Houston,USA,2004,1:633-640.

[2]Claudio Marcio Silva Dantas,Marcos Queija de Siqueira,Gilberto Bruno Ellwanger,Ana Lucia F.Lima Torres,Marcio Martins Mourelle.A frequency domain approach for random fatigue analysis of steel catenary risers at Brazil’s deep waters[C]//Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering-OMAE.Houston,USA,2004,1:199-209.

[3]金庆焕.深水油气是当今海洋油气勘探的主要热点[J].科学中国人,2006(11):18-19.

[4]李清平.我国海洋深水油气开发面临的挑战[J].中国海上油气,2006,18(2):130-133.

[5]Mekha B B.New frontiers in the design of steel catenary risers for floating production systems[J].Journal of Offshore Mechanics and Arctic Engineering,2001,123:153-158.

[6]Irani M B,Modi V J,Welf F.Riser dynamics with internal flow and nutation damping[C]//Proceeding 6th International Offshore Mechanics and Arctic Engineering Conference.Houston,USA,1987,3:119-125.

[7]林海花,王言英.波流共同作用下隔水管动力响应非线性分析[J].船舶力学,2009,13(2):189-195.

Lin Haihua,Wang Yanying.Analysis of nonlinear dynamic responses for marine riser induced by waves and currents[J].Journal of Ship Mechanics,2009,13(2):189-195.

[8]Chucheepsakul S,Monprapussorn T,Huang T.Large strain formulation of extensible flexible marine pipes transporting fluid[J].Journal of Fluids and Structures,2003,17:185-224.

[9]Sparks C P.The infuence of tension,pressure and weight on pipe and riser deformations and stresses[J].ASME Journal of Energy Resources Technology,1984,106:46-54.

[10]Huang T.Kinematics of transported mass inside risers and pipes[C]//Proceeding of 3rd International Offshore and Polar Engineers.Singapore,1993,2:331-336.

[11]Chucheepsakul S,Huang T,Monprapussorn T.Influence of transported fluid on behavior of an extensible flexible riser/Pipe[C]//Proceeding of 3rd International Offshore and Polar Engineering.Brest,France,1999,2:286-293.

[12]Leklong J,Chucheepsakul S,Kaewunruen S.Dynamic responses of marine risers/pipes transporting fluid subject to top end excitations[C]//Proceeding of 8th ISOPE Pacific/Asia Offshore Mech Symposium.Bangkok,Thailand,2008:105-112.