基于MHMM模拟电路早期故障诊断

2012-06-07朱凤波吴文全

电光与控制 2012年1期

朱凤波，吴文全，杨华

(海军工程大学，武汉 430033)

0 引言

模拟电路的故障诊断始于20世纪60年代，理论研究是从网络元件参数可解性开始的，常用的有故障字典法和参数辨识法，但电路故障的多样性、元件的容差及结构的复杂性，使得模拟电路故障诊断发展比较缓慢。20世纪90年代后，模糊理论、神经网络以及支持向量机等智能机器学习语言开始应用于该领域，取得不错的效果。但上述方法都是在硬故障(即元件断路或短路)时效果明显，软故障需在元件变化较大时才能有效识别［8］。

隐马尔科夫模型是一种广泛应用于信号处理和模式识别的双重随机过程，具有很强的时序信号识别和分类能力，已成功应用于语音识别和人脸识别领域。按照观测信号的性质可分为两类:连续隐马尔科夫模型(CHMM)和离散隐马尔科夫模型(DHMM)［2］。文献［3］提出将HMM应用于电路系统的状态检测及故障诊断;文献［4］基于HMM具有很强的时序信号识别能力，对HMM在机电系统BIT抗虚警技术方面进行了研究，通过训练DHMM来区分虚警与故障;文献［5］将HMM应用于故障预测与设备退化研究。本文在以上研究成果的基础上，尝试将高斯混合隐马尔科夫模型(MHMM)引入模拟电路的早期故障诊断，通过LDA(线性判别分析)方法对原始电路信号进行处理，完成降维，去除信号的冗余信息，然后通过MHMM模型对故障的类别进行判定。

1 MHMM模型

1.1 高斯混合模型模型介绍

高斯混合模型［6］(Gaussian Mixture Model，GMM)是一种常用的描述混合密度分布的模型，即多个高斯分布的混合分布。GMM本质上是一种多维概率密度函数，一个具有M个混合成分的D维GMM，可以用M个高斯成员的加权和来表示，即

其中:μi为均值;Σi为协方差矩阵。这里共有M个高斯分布，每个函数用 λi表示，i=1，2，…，M，其参数为μi和Σi。每个函数受P(λi)加权后，取和得到xn的概率分布。

整个高斯混合模型便可以由各均值矢量、协方差矩阵及混合分量的权值来描述，因此得到一个GMM模型参数θ，表示为

1.2 MHMM模型的基本原理

隐马尔科夫模型［3］(Hidden Markov Model，HMM)是一种基于马尔科夫链发展而来的不完全数据的统计模型，它有3个基本问题需要解决:评估问题，即给定模型和观测序列求最大似然值;解码问题，给定模型和观测序列求具有产生该序列最大概率的状态序列;学习问题，给定观测序列的训练集估计产生该训练集最大概率的模型。

MHMM模型［5］是常规离散HMM在观测序列为连续密度分布信号时的一种延伸。连续密度分布的HMM模型假定被观测的特征向量按某种概率密度分布，这种模型性能的好坏取决于假定的概率分布是否符合实际情况。一般来说，一些常用的概率分布函数很难单一地描述一组数据的分布情况，于是提出高斯混合HMM模型(Gaussian of Mixture HMM，MHMM)，即用几个中心不同，离散度不同的高斯分布组合逼近实际的特征向量分布。

为了应用连续观测密度，必须在模型的概率密度函数的形式上加上一些限制，来保证概率密度函数的参数以连续的方式重估。最普通的表达式为

其中:cjm为状态j的第m个混合分量的系数，也就是混合增益因子;τ为高斯混合密度概率;μjm和Ujm分别为状态j在第m个混合分量的均值向量和协方差矩阵。

由于高斯混合理论比较成熟，一定条件下能够拟合任何形式的分布，因此MHMM归结为首先用GMM方法对原始特征向量进行逼近，确定出高斯混合密度函数，然后将混合分量假定为观测序列进行处理的一种HMM模型。

2 特征向量的提取

从电路采集的数据具有很强的冗余性和复杂性，如果直接用于HMM的训练，不仅效果会降低，而且增大训练的复杂程度。通过LDA技术对原始数据进行降维处理，可以提高运算速度和精度。

线性判别分析(Linear Discriminant Analysis，LDA)是一种用于分类问题的维度归约的监督的方法，目前已被广泛应用于人脸识别技术。它是基于Fisher准则，寻找一组将高维样本投影到低维空间的最佳判别投影向量，使所有的投影样本类内离散度最小且类间离散度最大，也就是在降维的同时将同一个类别的样本尽量聚集，不同类别尽量分开［7］，即:寻找一个矩阵W，线性变换原始样本x，使得z=WTx，且

最大。式中:SB为类间散度矩阵;SW为类内散度矩阵。定义

3 基于MHMM的故障诊断流程

1)特征提取。原始数据信号经LDA降维，得到低维的特征向量并且分为训练数据和测试数据两部分，并分别组成观测序列。

2)模型训练。对模型参数初始化，将不同故障状态的特征向量训练数据送入MHMM模型，得到不同状态的故障模型。

3)故障辨识。将待测数据分别通过每种故障状态模型，求出其最大似然估计值，比较该值与各训练模型最大似然值的差值，最小者为该数据所处的故障状态。

MHMM故障诊断流程如图1所示。

图1 MHMM故障诊断流程图Fig.1 Flow chart of fault diagnosis based on MHMM

4 试验例证与结果分析

本文实验数据通过Multisim获得，如图2所示。

图2 低通有源滤波器Fig.2 Circuit of active low-pass filter

图2为有源低通滤波器，其中电阻容差为5%，电容容差为10%，通过蒙特卡罗分析，如图3所示。

图3 测试点蒙特卡罗分析Fig.3 Analysis of testing points based on Monte Carlo method

由图3可见，电阻电容的早期较小变化对于10～100 kHz频率之间影响最为明显，因此选取100 Hz、1 kHz、10 kHz、12.5 kHz、20 kHz、25 kHz、30 kHz、40 kHz、50 kHz、80 kHz、100 kHz、125 kHz、500 kHz 对应的数值组成13维原始数据向量。设定电路有正常、R1升高10%、R1降低10%、R2升高10%、R2降低10%、C1升高10%、C1降低10%、C2升高10%、C2降低10%共9种状态，每种状态分别进行100次蒙特卡罗分析，得到100组原始数据向量。通过LDA算法对原始数据向量进行处理，降为5维的特征向量。如图4所示，经LDA降维以后，取特征值最大的两列数据作图，可以明显地发现，数据不仅实现了降维，而且在一定程度上对类别进行了初步的划分。R2阻值增大与R1阻值增大基本重叠在一起，R2阻值降低与R1阻值降低也很难区分，比较符合电路的实际情况。

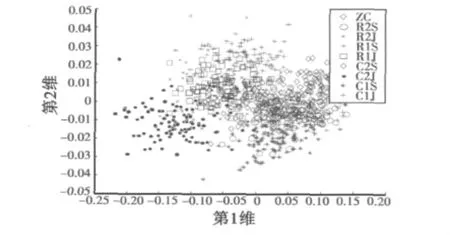
图4 原始数据经LDA降为2维时样本Fig.4 The sample dimension decreased by LDA

将每种状态下的100组特征向量取50组作为训练数据，每5组组成一个观测序列，共10组训练观测序列。同样，另外50组特征向量作为测试数据，每5组组成一个观测序列，共10组测试观测序列。9种电路状态共需训练9个MHMM模型，特征向量由3个高斯模型混合组成，HMM状态数设为5，由电路特性确定HMM结构采用左右型［1］，初始状态为正常，则初始矩阵为［1，0，0，0，0］，状态转移矩阵为［0.5，0.5，0，0，0;0，0.5，0.5，0，0;0，0，0.5，0.5，0;0，0，0，0.5，0.5;0，0，0，0，1］。GMM 高斯混合模型采用K均值法对观测序列进行逼近［2］，确定其参数。MHMM训练的E-M算法迭代次数［3］设为50，波动容差为1e－4，如图5所示。