推移质低输沙率
2012-06-07徐俊锋韩其为方春明
徐俊锋,韩其为,方春明
推移质低输沙率
徐俊锋,韩其为,方春明
(中国水利水电科学研究院泥沙研究所,北京 100048)
针对泥沙运动统计理论建立的推移质低输沙率公式进行了系统的描述,讨论了以拖曳力和平均流速为主要参数的两类推移质输沙率公式.指出了两类公式存在的问题.在揭示推移质输沙机理的基础上,提出影响输沙率大小的主要因素是泥沙输移的强度效应和速度效应.尽管各类输沙率公式都可以归结为这两个因素的共同作用,但只有考虑泥沙运动的随机因素才能正确概括泥沙起动时的低输沙率过程,才能明确起动时低输沙率的物理机理.
推移质;低输沙率;起动概率
【主编特邀】——河流泥沙运动理论
专家点评:河流作为地球系统过程中的重要组成部分,与人类命运息息相关.在漫长的历史过程中,河流刻化地貌、塑造平原,孕育了人类文明.随着经济和社会的快速发展,我国陆续对许多河流进行了梯级开发和利用,然而对河流充分开发利用带来经济和社会效益的同时,仍存在许多问题,需要进一步深入研究.
河流泥沙运动研究作为河流问题的核心内容,一直是学术界和工程界广泛关注的热点和焦点.随着长江三峡和黄河小浪底等大型水利枢纽工程的相继建成,河流泥沙领域中所包含的河势演变、河道重塑及学科交叉引发的河流健康、河流生态等问题逐步成为研究的重点和难点.
经过一代代科技工作者一个多世纪以来的探索和实践,我们在河流泥沙方面取得了丰硕的研究成果,并逐步形成了泥沙运动力学的基本理论.但由于泥沙运动具有随机性和复杂性的运动特点,以往的理论成果多建立在经验和半经验的基础上,研究难度较大,使得河流泥沙运动研究步入瓶颈阶段,近几十年来甚少突破性进展.
河流泥沙运动分为推移质运动和悬移质运动,泥沙在水流的作用下起动,首先发生推移质运动,随着水流作用的不断增强,逐渐开始出现悬移质运动.推移质运动和悬移质运动始终是国内外泥沙学者研究的热点.而推移质运动由于发生于床面附近,水流和泥沙的相互作用明显,难以对其进行直接观测,使得推移质运动机理逐渐成为泥沙运动研究的难点,亟待更深层次地研究和论证.
天然河流泥沙均为非均匀沙,非均匀沙颗粒之间及颗粒与水流之间的相互作用机理复杂.基于以上原因,现阶段河流泥沙运动的研究对象多选择均匀沙,对非均匀沙的研究更多的是在均匀沙公式的基础上进行修正;且现场观测实现困难,实验研究手段多为室内水槽研究,存在很大的局限性.随着工程建设中泥沙问题的不断暴露以及学科持续发展遭遇瓶颈亟需突破,迫切需要针对非均匀泥沙运动展开更加系统深入地研究,建立适应学科发展、满足工程应用的非均匀泥沙运动理论模式.非均匀泥沙运动机理和非平衡输沙已然成为目前泥沙研究的主题.
本期选登的几篇文章涉及山区河流推移质运动、非均匀泥沙起动和输移规律、推移质低输沙等几个方面,既有对推移质运动机理的研究和探索,也有对野外推移质运动的现场观测实验,属于河流泥沙运动研究关注的重点领域.此次以非均匀泥沙运动为主题刊出,希望对广大读者有所帮助,也请继续关注非均匀泥沙运动研究进展,以期共同进步.
天津大学 白玉川
推移质输沙过程是一个非常复杂且重要的问题,对此研究已取得不少有益成果,如以拖曳力为主要参数的公式[1-6],以流速为主要参数的公式[7],以及泥沙运动统计理论[8]等.各类成果的获取途径不尽相同,公式形式存在差异.为了揭示推移质的输沙特性,使这个问题更清晰和深化,笔者总结了几类公式中影响推移质输沙率大小的主要因素后,经过推导和计算,指出基于泥沙运动统计理论建立的公式可以正确地概括泥沙起动时的低输沙率过程.
1 统计理论低输沙率公式
一般条件下床面多颗泥沙起动的统计规律不论对于低输沙率、还是高输沙率都是适用的.这时的起动是一种广义的概念,指的是泥沙由静转动,其中包括了由静转滚、转跳及转悬3种,并不限于输沙率很低的情况.而推移质低输沙率是指床面泥沙处于“起动”状态时的输沙率.故此时泥沙运动只涉及到推移质颗粒的滚动运动.文献[1-6]认为泥沙起动时不存在输沙率,整个断面的输沙率为零.实际上泥沙起动时便发生了输移,只是输沙率的值很小而已.
基于泥沙运动统计理论的低输沙率研究,是以床面泥沙的起动强度λ为切入点的,它的物理意义是单位面积、单位时间起动的泥沙颗数.以一个泥沙颗粒为研究对象,λ与起动概率1ε成正比,而与颗粒起动时在床面停留的时间0t成反比,即单颗起动强度为.当单位床面颗粒密实系数为0k时,单位床面颗数,假定这0n颗泥沙的起动相互独立,则起动强度.当床面泥沙处于低输沙率的“起动”状态时只需考虑泥沙的滚动.起动强度λ就等于由静转滚强度,在整个的滚动过程中颗粒与床面是接触的,设起动时间为0,2t,即颗粒在床面的滚动时间.设滚动颗粒平均速度为2U,单步滚动距离为2l,则从而在单位床面、单位时间由静转滚颗粒的质量[8-9]为

式中sγ为泥沙容重,类似可推求在单位床面、单位时间由滚转静颗粒的质量为

式中bq为推移质单宽输沙率.在平衡条件下,式(1)和式(2)应相等,由此得到
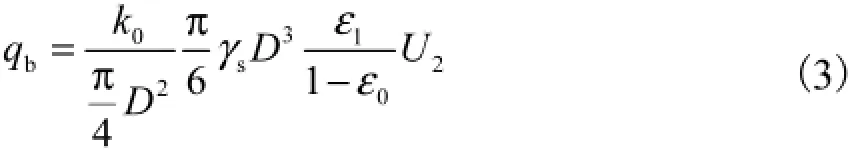
式中:单位床面泥沙静密实系数0k取0.4;1ε、0ε分别为起动概率和不止动概率;运动速度(对于低输沙率是滚动速度)[10]为
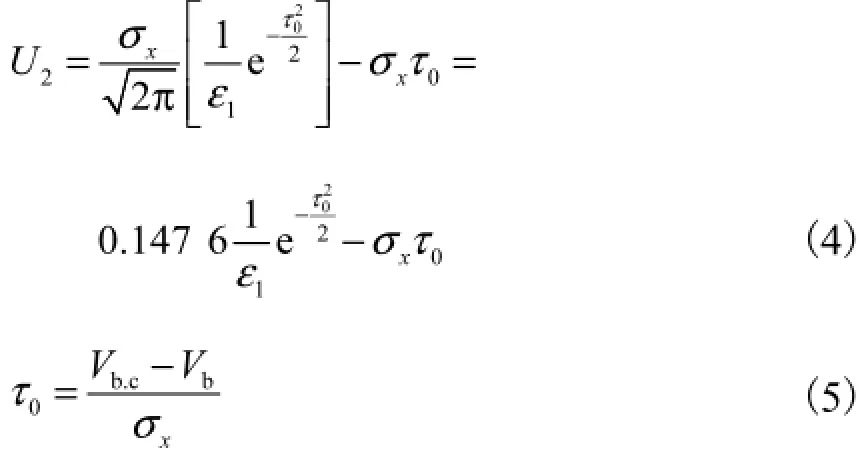
根据统计理论低输沙率公式的物理机理是明确的,可以理解成:为床面单位面积静止泥沙的颗数;为静止泥沙的质量.则表示在床面单位宽度、长为单次距离的面积上静止泥沙的质量,进而表示在该面积上起动的泥沙质量.故相当于2,0t时间段内推移质输沙量.即为床面上推移质的质量,再乘以平均速度2U遂得推移质输沙率式(3).
2 以拖曳力和流速为主要参数的推移质输沙率公式
2.1以拖曳力为主要参数的推移质输沙率公式
分析此类公式总结得出:①公式中推移质输沙率基本与拖曳力的3/2次幂或流速的3次幂成正比,所以该类公式主要反映输沙强度较高的情况而不能包含泥沙起动时的低输沙率过程;②此类公式都含有项来判断泥沙是否起动,进而计算输沙率的值.但这些项表明输沙率有明显的零点,故不能反映出起动流速试验时是有输沙率(尽管很小)的实际现象;③这类公式为了反映泥沙起动时输沙率相对变幅很大的特点,输沙率公式中切应力项的方次就要很高.韩其为[10]从理论上给出了当低输沙率接近零时,θ函数方次n可以大于27(流速方次为54).
2.2以流速为主要参数的推移质输沙率公式
此类公式的一般形式为

式中:K为系数;sγ为容重;V为流速;cV为起动流速;h为水深;n为指数.从式(6)可以看出:①推移质输沙率与水流速度的4次幂成正比,相当于与水流拖曳力的平方成正比,这与前面的3/2次幂是不一致的.②动密实系数是很难被证明的,且是造成前述两种推移质输沙率与推曳力方次不一致的原因.③这类公式中流速、水深、粒径等容易测量,较拖曳力参数公式中不易确定坡降J是其使用方面的一个优点.
3 推移质运动强度及推移质运动速度
从推移质输沙率的概念上看,决定其大小的主要因素是运动强度(颗数)和运动速度.
3.1推移质运动强度
推移质运动强度的变化范围很大,例如在一定时期内,泥沙颗粒数可以从一颗增加至大量,特别是在低输沙率阶段,颗数增加非常快.而泥沙颗粒的增加速度只能与水流速度保持线性关系,故不会在输沙率低时泥沙颗粒数增长很快.因此泥沙起动时输沙率突增的根本原因应是推移质运动强度的大范围快速变化,而以拖曳力和平均流速为主要参数的两类公式取细微变化的水流流速或颗粒滚动速度的高次方来衡量泥沙起动时输沙率的突增应该是有疑问的.
相比之下统计理论的低输沙率公式推导过程严密,各项参数有更明确的物理意义:从式(3)中可以看出能代表推移质颗数的多少或者说表示低输沙率公式中的运动强度效应(而2U则为公式中的运动速度效应).对于一定粒径的均匀沙,运动强度只与成正比,而处于起动状态的颗粒其不止动概率ε0,与“1”比较很小,有时可以忽略.在表1中,列出了不同相对底部流速Vbω1对应的相对输沙率λqb、起动概率ε1及相对跳跃速度U2ω1.可见当Vbω1在0.15~0.6时,U2ω1变幅仅2个数量级,起动概率1ε的变幅则有17个数量级,故bqλ有18个数量级.这说明:①低输沙率时bqλ的大幅度变化主要是起动概率(或者说是推移质运动强度)的大范围变化引起的,而不是由滚动速度2U变化引起.②尽管表1的数据显示输沙率已经很小,但是输沙率仍无零点,这是因为1ε和2U均不为零,这也说明泥沙起动时已存在输沙的现象(尽管很小).
3.2推移质运动速度
首先,从统计理论低输沙率式(3)可以看出无因次输沙率与颗粒运动速度2U成正比,这符合低输沙率过程.
其次,按确定性观点可得出颗粒运动速度与水流底部流速和起动水流底部流速之差成正比,即U=Vb-Vb,c.但如若考虑水流泥沙运动的随机特性,颗粒运动速度的数学期望应该是限于运动颗粒的一种条件期望.

表1 均匀沙各参数值Tab.1 Parameters of uniform sediment
韩其为[10]得到的颗粒滚动速度2U的条件期望为

式中:σx为纵向脉动流速的均方差,σx=0.37,为底部平均流速;Vb,c为起动流速;τ0为无量纲数,

从而有



图1 起动颗粒参数关系Fig.1 Parameter relations of initiation particles
将无量纲数τ0与参数K1、K2的关系绘入图1.结合图1得出:①作用在颗粒上的水流速度满足正态分布的随机变量,它的瞬时值Vb和时均值Vb可以小于起动速度Vb,c,以Vb,c=Vb为界可为正也可为负,当Vb,c<Vb时τ0为负,否则为正.这比力学分析法中按必然关系得到的颗粒运动时Vb恒大于Vb,c,τ0总大于零要符合实际.②按确定性观点得出的颗粒运动速度与水流底部流速和起动水流底部流速之差成正比即U2=Vb-Vb,c是片面的.因为当-2.70< 0τ<-1.00时,与1很接近,在此区域内U2=K1(Vb-Vb,c)=Vb-Vb,c正确,但当-1.00<τ0<1.00时,Vb,c与Vb很接近,K1的绝对值与1差别很大,U2=K1(Vb-Vb,c)≠Vb-Vb,c.因此可以得出U2=K1(Vb-Vb,c)与U2=Vb-Vb,c有很大的区别,即按确定性观点得出的颗粒运动速度等于水流平均底部流速与起动水流底部流速之差这一结果是有局限性的.③随0τ的增加,2K也单调增加,且变化均匀.较K1的无穷间断变化,K2变化稳定,且恒大于1.更主要的是K2反映了泥沙起动时的重要机理:①颗粒滚动速度U2实际上为作用其上的水流瞬时速度Vb=K2Vb与其起动速度Vb,c之差.②K2恒大于1,说明水流对泥沙作用的瞬时速度Vb=K2Vb总要大于水流平均底速Vb.③K2有非常明确的物理意义.例如,当τ0=2.69时,Vb,c=1.996,3Vb,泥沙要满足起动,则作用其上的流速是要大于Vb,c=1.996,3Vb的,而Vb=K2Vb=2.03Vb.
4 结 论
(1) 两类以拖曳力和流速为主要参数的公式对推移质的输沙机理阐述不够,推导过程不严格,尤其不适用于描述泥沙起动时的低输沙率过程,但从工程角度看,两类推移质输沙率成果对解决实际问题起了很大作用.
(2) 泥沙运动具有随机性,泥沙运动统计理论的引入,描述了随机因素的随机变量,故可以更好地从机理上阐述泥沙运动过程,这包括了本文研究的推移质低输沙率过程.
(3) 泥沙起动时细微变化的水流速度或颗粒滚动速度不应引起输沙率的很大波动,真正引起这种变化的是泥沙颗粒的起动概率1ε.
(4) 起动时颗粒滚动速度U2实际应为作用其上的水流瞬时速度Vb=K2Vb与其起动速度Vb,c之差,且K2有明确的物理意义.
[1] Meyer-Peter E,Muller R.Formulas for bed-load transport[C]// IAHR 2nd Meeting. Stockholm,Zurich,1948:39-64.
[2] Yalin M S. Mechanics of Sediment Transport[M]. UK:Pergamum Press,1972.
[3] Zanke Ulrich C E. On the physics of flow-driven sediment(bed-load)[J]. International Journal of Sediment Research,2001,16(1):1-18.
[4] Wu Baosheng,Molinas Albert,Shu Anping. Fractional transport of sediment mixtures[J]. International Journal of Sediment Research,2003,18(3):232-247.
[5] Wang Xingkui,Li Danxun,Qu Zhaosong,et al. Verification and comparison formulas for bed load transport[J]. Journal of Hydrodynamics,2001,13(1):8-11.
[6] De Sutter Renaat,Rushforth Peter,Tait Simon,et al. Validation of existing bed load transport formulas using in-sewer sediment[J]. Journal of Hydraulic Engineering,ASCE 2003,129(4):325-333.
[7] 中国水利学会泥沙专业委员会. 泥沙手册[M]. 北京:中国环境科学出版社,1989.
Sediment Professional Committee of Chinese Hydraulic Engineering Society. Sediment Manual[M]. Beijing:China Environmental Science Press,1989(in Chinese).
[8] 韩其为,何明民. 泥沙运动统计理论[M]. 北京:科学出版社,1984.
Han Qiwei,He Mingmin. Statistics Theory of Sediment Motion[M]. Beijing:Science Press,1984(in Chinese).
[9] 韩其为. 泥沙起动规律及起动流速[J]. 泥沙研究,1982(2):11-26.
Han Qiwei. The incipient disciplinarian and incipient velocity of sediment[J]. Journal of Sediment Research,1982(2):11-26(in Chinese).
[10] 韩其为,何明民. 泥沙起动规律及起动流速[M]. 北京:科学出版社,1999.
Han Qiwei,He Mingmin. The Incipient Disciplinarian and Incipient Velocity of Sediment[M]. Beijing:Science Press,1999(in Chinese).
Low Transport Rate of Bed Load
XU Jun-feng,HAN Qi-wei,FANG Chun-ming
(Department of Sediment Research,China Institute of Water Resources and Hydropower Research,Beijing 100048,China)
A systematic description of low transport rate formula was given based on statistical theory of sediment transportation, two bed load transport rate formulas with the main parameters being drag force and average flow velocity were discussed, and some defects in these two formulas were pointed out. On the basis of revealing the bed load transport mechanism, the main factors affecting the transport rate were presented as being strength-effect and speedeffect of sediment transport. Although various transport rate formulas all come down to the interaction between the two factors, only by considering stochastic factors of sediment movement can we properly summarize the low sediment transport rate of sediment start-up process and clear physical mechanism of low sediment transport rate.
bed load;low transport rate;incipient probability
TV142.31
:A
:0493-2137(2012)03-0191-05
2011-06-29;
2011-11-03.
水利部公益性行业专项基金资助项目(2009001003).
徐俊锋(1983— ),男,博士研究生,15210871984 @139.com.
韩其为,中国工程院院士,wangch@iwhr.com.
