超宽带系统中基于时域插值和抽取的新型Sigma-Delta转换器

赵迎新，向 坤，李艳红，吴 虹

超宽带系统中基于时域插值和抽取的新型Sigma-Delta转换器

赵迎新，向 坤，李艳红，吴 虹

(南开大学信息技术科学学院，天津 300071)

无线通信系统中，超宽带(UWB)与正交频分复用(OFDM)技术相结合，具有超宽带、低功耗、抗多径衰落等优势．针对多频带OFDM-UWB信号的特点，提出一种基于时域插值和抽取的新型sigma-delta转换器用于完成数据的转换．时域插值使得多频带OFDM-UWB子载波间形成空隙，sigma-delta调制器将输入信号量化为1比特数据流的同时完成量化噪声整形．该sigma-delta调制器在量化噪声频谱中引入位于多频带OFDM-UWB子载波频点上的零点，将大部分量化噪声推到子载波空隙中，达到噪声整形效果．新型sigma-delta调制器采用无过采样结构，使得硬件实现相对容易，同时该结构还避免了OFDM系统的高峰均比问题．对信号进行时域插值与抽取降低了硬件复杂度和处理时间．理论分析和仿真结果表明了该调制器的有效性和可行性．

超宽带；时域插值和抽取；sigma-delta调制

超宽带(ultra wide band，UWB)信号定义为相对带宽(信号带宽与中心频率之比)大于0.25，或绝对带宽不小于500,MHz的信号．与现有的窄带系统相比，UWB信号具有极宽的带宽和极高的数据速率，同时具有低功耗、抗多径衰落能力强和保密性强等特点[1]，这些优点使其在无线通信方面具有很大的潜力．正交频分复用(orthogonal frequency division multiplexing，OFDM)是一种多载波传输技术，通过相互正交的子载波并行传输数据，是一种高效的数据传输方式．IEEE 802.15.3,a[2]和ECMA—368[3]标准建议将UWB和OFDM技术相结合，可成为短距离、高数据率无线网络理想的传输/接入方案之一．

然而，随着UWB技术的快速发展，传输速率及带宽将不断增加，多频带OFDM超宽带系统对信号处理速度、采样速率、数模(digital-to-analog，D/A)和模数(analog-to-digital，A/D)转换器的要求都将大大提高．文献[4]研究了传统的以现有sigma-delta调制器为核心的数据转换器，对于多频带OFDM-UWB系统来说，已经无法满足其性能要求．

笔者提出一种基于时域插值和抽取的新型sigma-delta调制器用于完成数据的转换．该调制器的噪声传递函数适合多频带OFDM-UWB信号，将大部分的量化噪声移到子载波空隙中，降低了信号带内的噪声功率，由于采样频率为奈奎斯特频率，使得硬件实现相对容易．

1 时域插值与抽取方法

根据多频带OFDM-UWB标准ECMA—368协议，信号经过信道编码后进行交织．经过QPSK调制后形成复信号X( k), k=0,…,N-1．信号

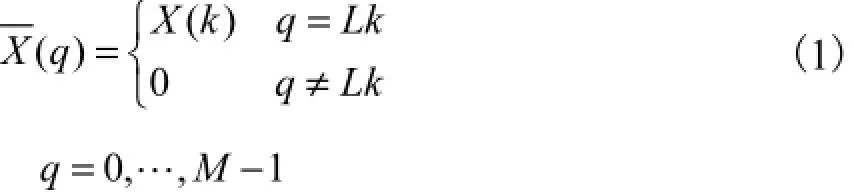
是在信号()X k的每2个数据间插入1L-个零而形成的复信号，其中，MLN=．经过M点IFFT 变换，多频带OFDM-UWB子载波间形成1L-个子载波间隔的空隙．经过IFFT变换后的信号为

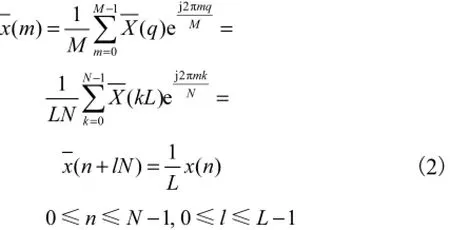
式中x( n)为X( k)进行N点IFFT变换的结果．由式(2)可知，信号( m)是以N为周期对x( n)重复L次的结果．基于以上分析，本文将经过QPSK调制后形成的复信号X( k), k=0,…,N-1，先进行N点IFFT变换后，再将得到的时域信号x( n), n=0,…,N-1，重复发送L次，即传输信号为

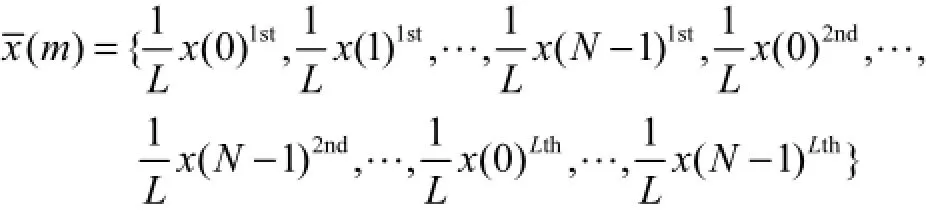
完成时域插值，同样能够使得多频带OFDM-UWB子载波间形成1L-个子载波间隔的空隙．

多频带OFDM-UWB信号经过sigma-delta调制后是包含有部分量化噪声的信号，即

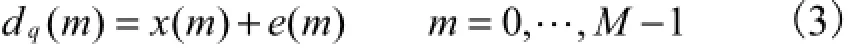
该信号可以表示成L个N维向量，即

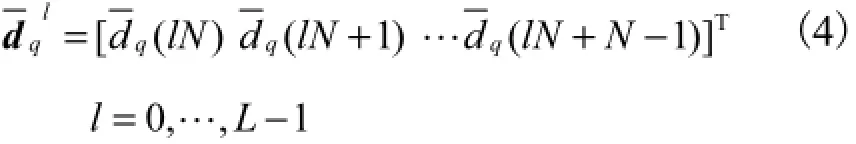
时域抽取将此L个向量中的元素一一对应相加，得N维向量为

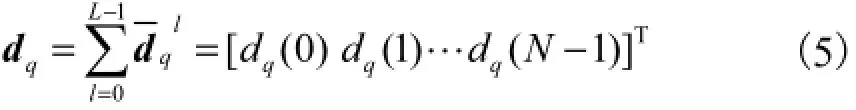
该信号经过N点FFT变换后为

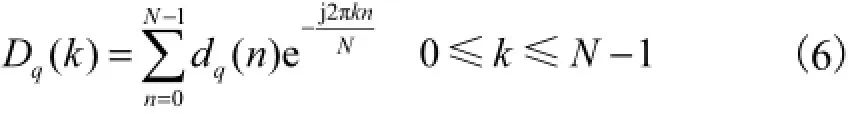
然后在接收端经过QPSK解调、解交织和译码等完成数据的恢复．

对多频带OFDM-UWB信号的时域插值和抽取工作在时域完成，IFFF和FFT的长度不受插值因子L的影响．时域插值和抽取省去了很多冗余计算，从而节省了时间和资源．

2 Sigma-delta调制器

2.1 Sigma-delta调制器原理

Sigma-delta数据转换器应用过采样和噪声整形技术对信号进行处理[5]，把信号带内的噪声推到高频端．Sigma-delta调制器是sigma-delta数据转换器的核心部分，又称总和增量调制器，它是数字通信系统中的一种波形编码调制技术．它将输入信号转化为1比特高时间分辨率过采样数据流，图1为传统的一阶1比特sigma-delta调制器．调制器的输出信号为

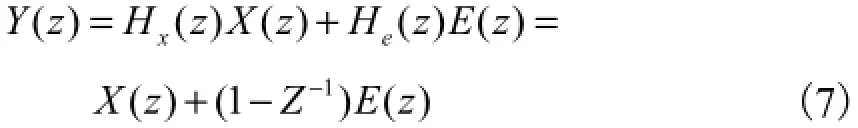
式中：x( z)和y( z)分别为调制器的输入和输出信号；Hx(z)为信号传递函数(signal transfer function，STF)，Hx(z)=1；He(z)为噪声传递函数(noise transfer function，NTF)，He(z)=1-z-1．从式(7)可以看到，调制器对信号没有影响，而对噪声，相当于引入了一个整形函数He(z)，图2为噪声传递函数的幅频特性．He(z)在频率f=0处有一个零点，在低频端噪声有很大的衰减，随着频率的增加噪声传递函数的幅度逐步增大．如果输入信号为窄带低通信号，则大部分量化噪声都分布在信号带外，可以通过合适的低通滤波器将量化噪声滤除．

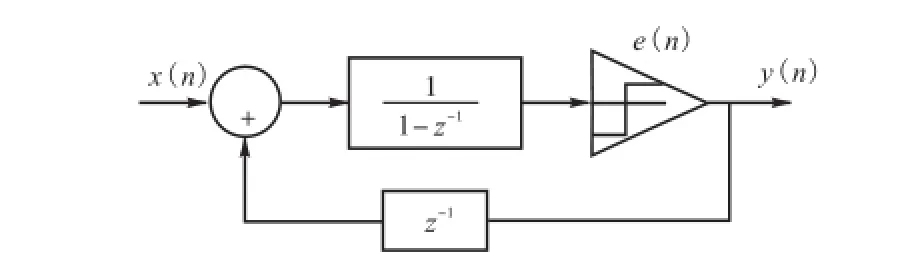
图1 一阶1比特sigma-delta调制器结构Fig.1 Structure of first order one bit sigma-delta modulator

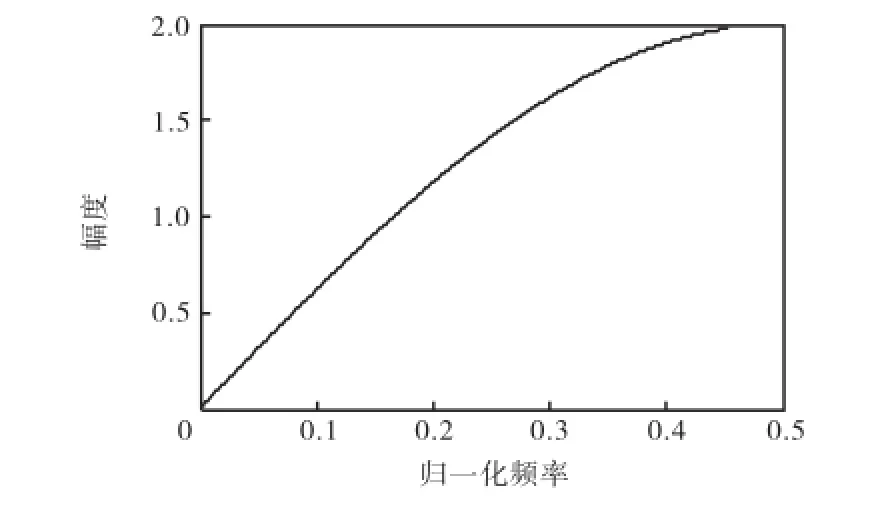
图2 一阶噪声传递函数幅频特性Fig.2 Magnitude characteristics of first order NTF

2.2 Sigma-delta调制器设计

在传统的sigma-delta D/A和A/D转换器中，输入信号需要以很高的采样频率进行过采样，对于超宽带的信号，很高的过采样率和采样频率是不切实际的，且不易于硬件实现．多频带OFDM-UWB信号可以看作是由多个以载波频点为中心频率的窄带信号正交叠加形成，且经过时域插值后，子载波间形成空隙，根据这个特点，对传统sigma-delta调制器的噪声整形技术加以修改，以避免采样频率过高的问题．修改后的调制器在量化噪声频谱中引入了N个零点，这些零点位于多频带OFDM-UWB子载波频点上，将大部分量化噪声推到子载波空隙中，即用量化噪声填补信号频谱中的空隙．此结构无需对信号进行过采样，调制器工作在奈奎斯特频率即可完成信号的转换．图3为本文提出的一阶sigma-delta调制器结构．调制器输出为

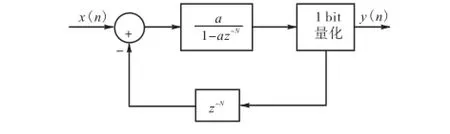
图3 N零点一阶sigma-delta调制器结构Fig.3 Structure of first order N zeros sigma-delta modulator

该结构在量化噪声谱的频点2πk/ N(k=0,1,…, N)处引入N个零点，图4为NTF的零极点分布(N= 16)，图5为量化噪声与信号频谱对比示意(图中以前6个子载波的情况为例)．量化噪声频谱中零点的位置正是子载波的频点位置，在零点处量化噪声急剧衰减，大部分量化噪声位于各子载波频带外，即两个子载波间的空隙中．

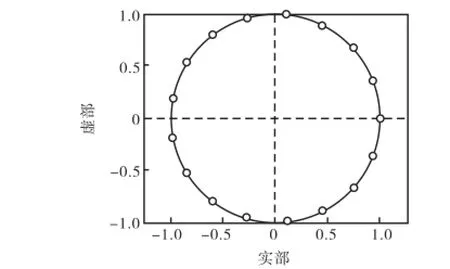
图4 NTF的零极点分布Fig.4 Pole-zero locations of NTF

图5 量化噪声与信号频谱对比Fig.5 Frequency spectrum of quantization noise and signal

为了更好地衰减子载波频带内的量化噪声，可以采用更高阶的调制器达到更好的噪声整形效果．图6为二阶sigma-delta调制器结构．STF和NTF分别为

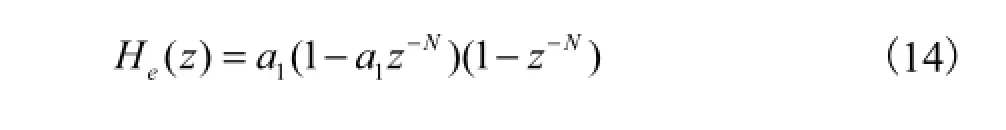
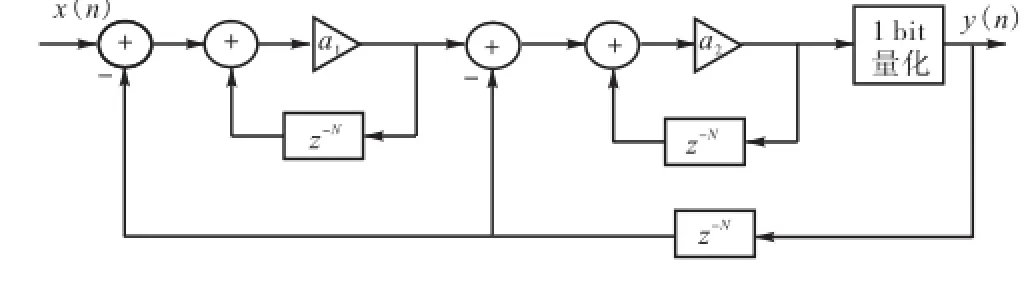
图6 N零点二阶sigma-delta调制结构Fig.6 Structure of second order N zeros sigma-delta modulator

2.3 量化间隔的优化

本文sigma-delta调制器中采用1比特量化器，它是一个非线性器件，可以将其近似理解为量化器输入信号与量化噪声的叠加．量化噪声有两种形式：一般量化噪声和过载量化噪声．当量化器的量化间隔为Δ时，在量化器输入不过载的情况下，量化误差满足e≤Δ/2，即量化误差信号在-Δ/2～Δ/2范围内变化，这种噪声被称为一般量化噪声．过载量化噪声发生在信号斜率陡变时，由于量化间隔Δ是固定的，量化后的信号波形可能会跟不上原信号的变化，形成包含很大失真的信号，这样的失真称为过载噪声．文献[6]对量化过程和量化参数的关系进行了细致的分析，指出可以适当增大量化间隔Δ和采样频率fs，以减小过载量化噪声，但是增大量化间隔Δ，将增大一般量化噪声，因此适当选取量化间隔关系到量化器性能的优劣．

由上文分析可知，sigma-delta调制器输入信号是以N为周期对x( n)重复L次的结果，即在一个符号周期内的传输数据为

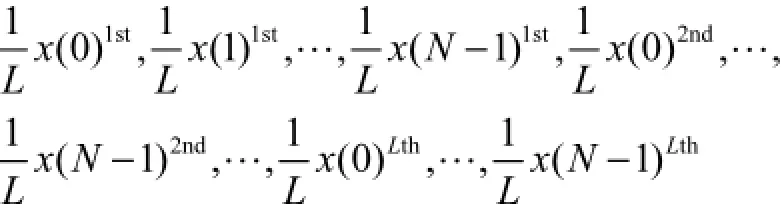
由于sigma-delta调制器包含有N个数据的环路延迟，因此在一个符号周期内，量化器的输入为相同数据重复L次，使得此量化器相当于输出为1L+个电平的量化器．例如，当4L=时，在一个符号周期内，量化器的输入为()x n重复4次，输出数据分为5种情况出现：4个1，3个1和1个0，2个1和2个0，1个1和3个0，4个0，这相当于五电平量化．

在已知量化器输入信号概率密度函数()p x条件下，可求出一组分层电平值kx与重建电平值ky，使量化误差的均方值最小，kx和ky的计算式为

在一般情况下式(15)和式(16)只能通过迭代方法求解．其基本步骤如下：

(1) 给定初始值y1，由式(16)在给定x1=0时求出x2；

(2) 由式(15)，根据x2、y1求出y2；

(3) 由式(16)，根据y2、x2求出y3．

重复步骤(1)～(3)，可求出{xk}和{yk}，然后代入式(16)验证xk+1=∞时，等式右边是否等于yL+1．若不等，则改变初始值，重复上述步骤，一直到式(16)两边的误差满足给定的容差值为止．根据上述方法得到sigma-delta调制器中1比特量化器的最佳量化间隔为

式中σ为多频带OFDM-UWB信号的均方差值．

3 多频带OFDM超宽带系统结构

图7为采用本文提出的sigma-delta 转换器的多频带OFDM-UWB系统结构，根据ECMA—368标准，传输数据经过信道编码后进行交织，以提高对突发错误的纠正能力．数字调制(如QPSK、MQAM)是为了引入多进制传输，使系统在相同符号传输速率的条件下，实现较高的信息传输速率．调制后的信号加导频和训练序列、IFFT和加零后缀等，形成基带信号．基带信号一帧由66个OFDM符号组成，每个OFDM符号由128个子载波组成，包含100个数据子载波、12个导频子载波、10个保护子载波和6个空子载波．基带信号在不同的时间被调制到3个子频带上传输．

在信号进入sigma-delta调制器之前进行时域插值，以保证在多频带OFDM-UWB子载波间形成空隙，插值后的信号不需要过采样，直接进入sigmadelta调制器，经过1,bit D/A转换器和模拟低通滤波器后在UWB信道中传输．接收端信号进行1,bit A/D转换，将模拟信号转换为数字信号后，用梳状滤波器滤除子载波间隔中的大部分量化噪声[7]，然后进行时域抽取，再进行与发送端对应的相反的操作，将从信道接收到的信息恢复出来．在系统仿真过程中，需要加入信道估计和均衡，以消除信道和滤波器对信号幅度和相位的影响．

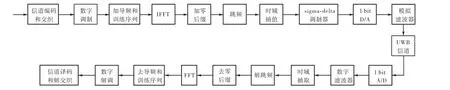
图7 多频带OFDM-UWB系统结构Fig.7 Structure of MB-OFDM-UWB system

4 仿真结果与分析

根据以上分析，本文对整个系统进行了仿真．系统采用本文提出的基于时域插值和抽取的一阶sigma-delta调制器，其中N=128，a=0.5．图8为当插值因子L=8时，时域插值后多频带OFDM-UWB信号频谱．图9为经过sigma-delta调制器后的信号频谱．由图9可知，经过时域插值后，多频带OFDMUWB子载波间形成了空隙，此时信号带宽为W=528 MHz ，即fb=264 MHz ，采样频率为fs= 2fb=528 MHz ，是信号的奈奎斯特采样率，sigmadelta调制器即在此频率工作．如图9所示，经过sigma-delta调制器后，大部分的量化噪声被推到信号带外，即2个子载波中间．经过调制器的信号可以在接收端通过梳状滤波器将子载波空隙中的大部分量化噪声滤除．

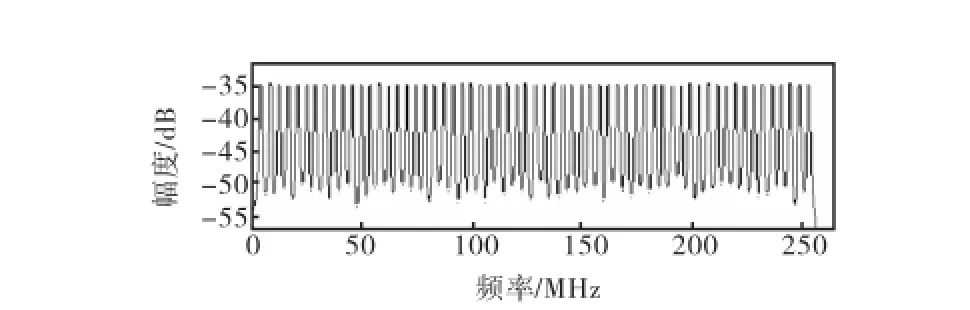
图8 时域插值后的信号频谱(L=8)Fig.8 Frequency spectrum of time domain interpolated signal(L=8)

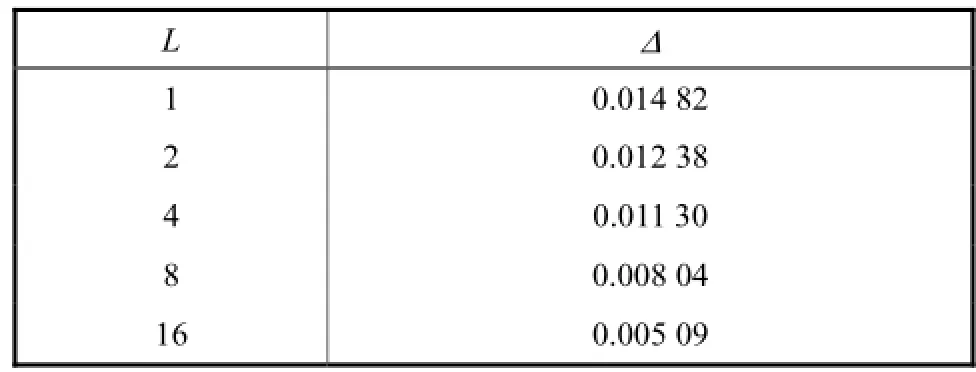
表1 最佳量化间隔Tab.1 Optimum quantization size

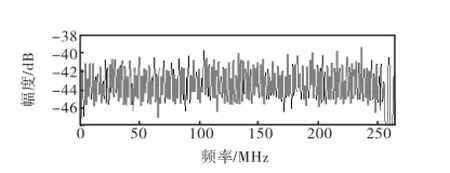
图9 经过sigma-delta调制器后的信号频谱Fig.9 Frequency spectrum of output signal of sigma-delta modulator

OFDM信号是经过调制的多个子载波叠加而成，可能产生比较大的峰均功率比[8]，要求功率放大器等器件具有很大的线性动态范围．本文提出的sigma-delta调制器由于采用1比特量化，输出为携带量化噪声的二进制信号，能够有效解决系统高峰均比问题．

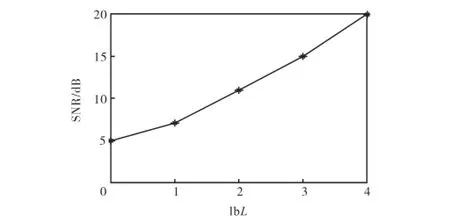
图10 插值因子与调制器信噪比关系曲线Fig.10 Interpolation factor vs SNR of modulator

由于OFDM时域信号呈高斯分布[9]，所以可以近似地认为多频带OFDM-UWB信号服从均值为0、方差为σ2的高斯分布．当系统采用QPSK数字调制方式时，仿真计算所得多频带OFDM-UWB信号的均方差σ=0.029 7．根据式(15)～式(17)计算在不同差值因子条件下的最佳量化间隔如表1所示．

图10为根据表1的量化间隔仿真得到的差值因子与调制器信噪比(signal-to-noise ratio，SNR)关系曲线，当插值因子由2提高到4时，改善的信噪比约为2.5,dB，随着插值因子的增大，SNR逐渐增大，sigmadelta调制器的性能提高．

根据仿真得到的误比特率，做出了多频带OFDM-UWB系统的差错概率图，如图11所示．根据插值因子的不同，得到不同的误比特率曲线，插值因子越大，子载波间空隙越大，带内量化噪声越少，调制器的信噪比越高，从而系统的性能越好．ECMA—368标准要求SNR为5,dB时，系统误比特率达到10-5．由图11可以看出，当系统误比特率为10-5，插值因子为4、8和16时，所需的信噪比为4,dB、1,dB和-1.8,dB，多频带OFDM-UWB系统可满足标准要求．

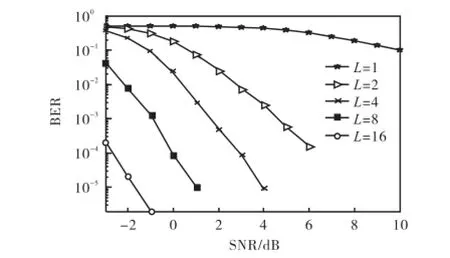
图11 超宽带系统的差错性能曲线Fig.11 Error performance curves of UWB system

5 结 语

针对多频带OFDM超宽带信号特点和频谱特性，本文提出了一种基于时域插值和抽取的sigmadelta转换器用于完成系统的数据转换．其中，sigmadelta调制器的量化噪声频谱中的多个零点与信号频谱相匹配，将大部分量化噪声推到信号的子载波空隙中，完成了量化噪声整形．调制器工作在奈奎斯特频率，保证了硬件电路的可实现性．仿真结果表明了该方法的可行性，为超宽带信号转换提供了一种有效的方法．

［1］ Batra A，Balakrishnan J，Aiello G R，et al. Design of a multiband OFDM system for realistic UWB channel enviroments[J]. IEEE Transactions on Microwave Theory and Techniques，2004，52(9)：2123-2138.

［2］ Batra A，Balakrishnan J，Dabak A，et al. IEEE P802.15-03/268r2 Multi-Band OFDM Physical Layer Proposal for IEEE 802. 15 Task Group 3a[S]. Piscataway：IEEE Press，2003.

［3］ Wi Media Alliance. TS102455V1.1.1 High Rate Ultra Wideband PHY and MAC Standard[S]. Geneva：European Computer Manufaturers Assaciation，2005.

［4］ Li Z，Fiez T S. A14 bit continuous-time delta-sigma A/D modulator with 2.5,MHz signal bandwidth[J]. IEEE Journals of Solid-State Circuits，2007，42(9)：1873-1883.

［5］ Engelberg S. Sigma-delta converters：Theory and simulation[J]. IEEE Instrumentation and Measurement Magazine，2007，10(6)：49-53.

［6］ Souryal M R，You H Q . Quantize-and-forward relaying with M-ary phase shift keying[C]//2008 IEEE Conference on Wireless Communications and Networking. Las Vegas，USA，2008.

［7］ Orfanidis S J. Introduction to Signal Processing[M]. New Brunswick：Pearson Education，2010.

［8］ Varahram P， Al-Azzo W F， Ali B M. A low complexity partial transmit sequence scheme by use of dummy signals for PAPR reduction in OFDM systems[J]. IEEE Transactions on Consumer Electronics，2010，56(4)：2416-2420.

［9］ Yang S H，Lu Y G，Gong L. Implementation of the programmable OFDM signal generator based on MCU[C]//2009 International Conference on Wireless Communication，Networking and Mobile Computing. Beijing，China，2009：2397-2412.

A Novel Sigma-Delta Converter Based on the Time Domain Interpolation and Decimation in UWB Systems

ZHAO Ying-xin，XIANG Kun，LI Yan-hong，WU Hong
(School of Information Technology Science，Nankai University，Tianjin 300071，China)

UWB-OFDM (ultra wide band and orthogonal frequency division multiplexing) in wireless communication systems offers several advantages, including robustness to multi-path interference, low power consumption and wide bandwidth. According to the signal characteristics, a novel sigma-delta modulator based on time domain interpolation and decimation was designed for multi-band OFDM-UWB signal conversion. The time domain interpolation resulted in the gaps between sub-carriers. The outputs of sigma-delta modulator were one bit binary streams that carried signal plus quantization noise. The sigma-delta modulator produced zeros in the quantization noise spectrum. These zeros were located at the frequencies of multi-band OFDM-UWB sub-carriers so that the quantization noise filled the gaps in the signal spectrum. Consequently, the presented non-oversampling sigma-delta modulator achieved hardware realization more easily. The large peak-to-average power ratio problem was eliminated in this structure. The time domain interpolation and decimation greatly reduced the complexity and saved the time. Theoretical analysis and simulation results were given to illustrate the validity and feasibility of the modulator.

ultra wide band；time domain interpolation and decimation；sigma-delta modulation

TN914.3

A

0493-2137(2012)07-0641-06

2011-06-15；

2011-10-12.

国家自然科学基金资助项目(60872026)；天津市应用基础及前沿技术研究计划重点资助项目(09JCZDJC16900)．

赵迎新（1983— ），女，博士，讲师，zhaoyingxin4074@gmail.com．

吴 虹，wuhong@nankai.edu.cn.