基于改进AES算法的无线射频识别安全研究＊

胡达海 张昌宏 刘 鹏

（海军工程大学电子工程学院 武汉 430033）

1 引言

无线射频识别（Radio Frequency Identification，RFID）技术是近年来随着无线电技术和大规模集成电路的普及应用而出现的一种先进的自动识别和数据采集技术［1］。RFID技术正以其方便快捷、稳定可靠的性能备受青睐，其在军事领域的应用越来越受到人们的普遍关注［2～3］。在军事装备保障中应用RFID技术，能够实现对装备保障的全过程实施实时追踪和指挥控制，随时随地准确调控战场装备物资的流量与流向，从而建立“精确型和快速反应型”装备保障系统，实现军事装备保障决策科学化和快速化，提高装备保障水平和效益。

由于在RFID系统中标签和阅读器之间采用无线射频通信的方式进行数据传输，同时标签的计算和存储资源都有限，因此系统很容易受到各类形式的攻击［4］。而且军事装备具有特殊性，所以在应用中RFID系统的安全性问题显得尤为重要。

2 实用RFID系统的安全性问题

2.1 RFID系统面临的攻击方式分析

针对RFID系统的攻击方式可分为主动攻击和被动攻击两种类型［1］。主动攻击主要包括：通过扫描标签和响应阅读器，寻找系统安全协议和加密算法的弱点，进而实施删除或篡改标签数据内容的攻击；通过干扰广播、阻塞信道或其它手段进行拒绝服务攻击等。被动攻击主要是采用窃听技术，通过分析系统工作过程中产生的各种电磁特征，获取标签与阅读器之间的通信数据。

2.2 RFID系统的安全需求分析

在装备保障应用中，对整个RFID系统的安全性要求十分高，设计的安全方法应满足以下几点要求：

1）认证：RFID系统的每个组成部分都应该进行认证。标签、阅读器和后端数据管理系统相互之间应进行相互的授权认证。认证就是验证所收到的消息确实来自真正的发送方且未被修改，它也可以验证消息的顺序和及时性。

2）机密性：用于安全协议的标准不能被泄露，只能由相互认证的用户共享这些标准；并且标签不能向未经授权的阅读器泄露任何信息。

3）真实性：阅读器必须确信消息是来自真正的标签，而不是经由攻击者伪造或篡改的标签。而标签的真实性是经由认证来确定的。

4）满足资源限制要求：在军事应用中，不但要考虑安全性，而且也必须要满足其工作效率、成本等方面的要求。

3 面向RFID系统的AES算法优化与设计

一个完善的RFID应用系统采用混合传输方式对信息的传输进行保护，即应该先认证后再加密。因此设计一个安全高效的加密算法是保证RFID系统安全的关键问题之一［7］。

现代密码算法主要分为对称密码算法和非对称密码算法，而对称密码算法比较简便、高效、密钥简短，破译极其困难，且能经受住时间的检验和攻击，正符合RFID系统要求的高效性和安全性。目前在对称密码算法中，AES算法具有设计简单，密钥安装快、需要的内存空间少，在所有平台上运行良好，支持并行处理，还可抵抗所有已知攻击，包括对抗已知分析攻击的能力，可以有效地实现抵抗差分密码分析、线性密码分析、删节差分分析、平方攻击和插值法分析等优点，已经开始应用于RFID系统中［5］。RFID系统应用下的AES算法的实现可分为硬件和软件两种方式。软件实现一般是通过在嵌入式处理器上运行编程后的算法，这种方法实现简单，成本低，但速度比较慢，安全性不高，而且机动性差；而硬件实现是通过具体的电子线路实现算法，加密速度比较快，安全性高，是目前主要的实现方法。但是如何才能快速、高效地实现AES加解密算法以及尽可能地节约资源降低成本，达到速度与占用资源的平衡，是目前需要解决的问题。

3.1 AES算法的数学基础

2000年10月2日，NIST宣布Rjindael作为新的AES［6］。它是一个迭代型分组密码，其分组长度和密钥长度都可变，各自可以独立指定为128比特、192比特、256比特。有限域中的元素可以用不同的方式表示。对于任意素数的方幂，都有唯一的一个有限域，因此GF（28）的所有表示是同构的，但不同的表示方法会影响到GF（28）上运算的复杂度，本算法采用传统的多项式表示法。将b7b6b5b4b3b2b1b0构成的字节b看成系数在｛0，1｝中的多项式。

1）有限域

有限域是指仅含有限多个元素的域，而有限域中元素的个数称为有限域的阶。对于有限域，其元素个数必然是素数的幂，而这个对应的素数成为有限域的特征。即m阶有限域存在当且仅当m是某素数的幂，亦即存在某个整数n和素数p，使得m＝pn。p称为有限域的特征，有限域记为GF（pn）。

2）有限域上的多项式

在有限域GF上定义如式（1）形式的多项式：

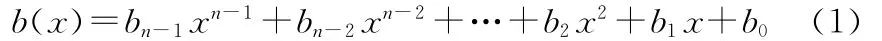
其中系数bi是有限域GF（p）中的元素，我们称b（x）是GF（p）中的多项式。

3）有限域上的运算

有限域上GF（28）的字节运算：

（1）字节加法：即两个多项式相同指数项系数逐项进行比特的模2加，也可以用异或操作来执行（用⊕表示）。例如对于两个用字节表示的多项式｛a7，a6，a5，a4，a3，a2，a1，a0｝和｛b7，b6，b5，b4，b3，b2，b1，b0｝，和记为｛c7，c6，c5，c4，c3，c2，c1，c0｝，可描述为ci＝ai＋bi，即c7＝a7⊕b7，…，c0＝a0⊕b0。

（2）字节乘法：两多项式进行相乘后再将结果对不可约分多项式m（x）取模，m（x）＝x8＋x4＋x3＋x＋1（用十六进制表示为｛01｝｛1b｝），模m（x）能保证多项式字节乘后的多项式始终在GF（28）上。

多项式系数在有限域GF（28）上的字运算：

（1）字加法：与字节加法有所不同，两个多项式相同指数项的系数不再是比特，而是一个字节，字的加法即相同指数项的字节系数的异或运算。例如对于两个用字表示的多项式｛a3，a2，a1，a0｝和｛b3，b2，b1，b0｝，和记为｛c3，c2，c1，c0｝，可描述为ci＝ai＋bi，即c3＝a3⊕b3，…，c0＝a0⊕b0。

（2）字乘法：两多项式进行相乘后再将结果对可约分多项式m＇（x）取模，m＇（x）＝x4＋1，模m＇（x）能保证多项式字乘后的结果仍是一个字。

4）有限域GF（28）上的xtime（）运算

有限域GF（28）上还定义了一个运算，称为x乘法，记做xtime（），定义如下：

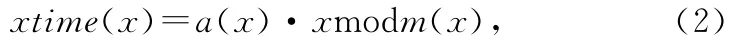
其中a（x）＝a7x7＋a6x6＋a5x5＋a4x4＋a3x3＋a2x2＋a1x＋a0，a（x）∈GF（28），m（x）＝x8＋x4＋x3＋x＋1。多项式xtime（）运算可以通过左移一位实现，如果左移后产生的新多项式级数大于7，则结果还应与m（x）进行模2加运算，使xtime（）结果始终在有限域GF（28）内。

3.2 AES算法结构设计

AES算法的硬件结构设计可以分为反馈方式和非反馈方式两种。反馈方式下，在一个或多个时钟周期内完成一轮迭代运算，并把运算结果送入寄存器保存下来作为下一轮迭代的输入，每一轮运算共享一个迭代结构，称为轮单元。非反馈方式通过复制轮单元，设置流水线站来提高系统时钟频率，从而进一步提高数据吞吐率。

常见的AES算法结构可以分为三种：完全流水线结构、内部流水线结构和循环迭代结构。

1）完全流水线结构属于非反馈方式，内部流水线结构和循环迭代结构属于反馈方式。完全流水线结构［7］由多路开关、寄存器和逻辑电路构成，将每个轮单位作为一级，级与级之间通过插入寄存器来设置流水线站，把整个过程划分为前后相连的多级实体，每级实体独立完成一级流水中所有的逻辑运算，互不影响，很适合采用电码本（ECB）作为AES算法的工作模式，能够在同一时刻对多个分组做运算，极大地提高了吞吐率。但是此种结构所占用的硬件空间和流水线级数成正比，其速度的增加是以资源的占用成比例增加为代价的，因此这种高代价限制了它在低成本低功耗的RFID系统的应用，只适合于网络应用等对速度有很高要求的场合。

2）内部流水线结构是指在轮单元中插入寄存器，将每个轮运算分成多个操作段，每个时钟周期内完成一个操作段。这种在轮单元内部采用流水线技术的结构能在一定程度上提高算法运行的时钟频率。但轮内各级流水部件无法同时执行，因此增加了算法运行的时钟数目。轮内流水线级数越多，时钟数目也就越多，虽然能够提高算法的时钟频率，但吞吐量并没有明显提高。

3）循环迭代结构是指通过模块复用技术，设计一个轮运算模块，对一个分组加密时，循环调用这个模块10次即可。这种结构是硬件代价最低的设计，所有迭代只用1个轮变换，10个时钟周期即可完成1个分组运算。这种结构下轮单元之间必须依次执行各自的操作，各轮操作无法同步进行，因此所需时钟周期比其它两种结构要长。

综上所述，由于文设计的AES算法是面向资源受限的RFID系统，目的在于尽量减少资源的占用，使面积尽可能减小。因此采用循环迭代结构作为算法所要设计的结构，由于循环迭代结构无法并行地处理多个分组，采用电码本（ECB）的工作模式无法体现工作模式本身的并行高速处理多个分组的优点且电码本（ECB）模式存在着相同明文产生相同密文的安全缺陷，因此在分组的工作模式上选择CBC反馈模式。

3.3 AES算法优化设计

由于AES算法解密过程跟加密过程并不相同，解密过程仅有一部分能使用与加密过程相同的电路来完成，因此为了最大限度地降低电路面积，必须先利用电路模块的复用技术对算法进行优化处理，使算法加解密电路可以复用。因此可以根据以下两种性质对加解密结构进行优化［8～9］：

1）行移位／逆行移位不改变字节的值，只是进行移位操作；而字节替换／逆字节替换只对状态中每个字节进行非线性替换，与字节的位置无关。因此行移位／逆行移位和字节替换／逆字节替换变换的顺序可以根据需要进行互换，而不影响最后结果。字节替换与逆字节替换均是仿射变换和乘法求逆变换的复合，因此可将乘法求逆作为两种变换的共用模块进行电路结构复用。

2）在数学上，对于一个线性变换，则满足A（X＋K）＝A（X）＋A（K），而在AES算法中，逆列混合运算是线性变换，因 此 也 满 足 如 下 公 式［10］：InvMixColumn（State⊕RoundKey）＝InvMixColumn（State）⊕InvMixColumn（RoundKey）。

应用如上两条性质，可以将加解密过程复合在一个结构中实现，如图1所示。

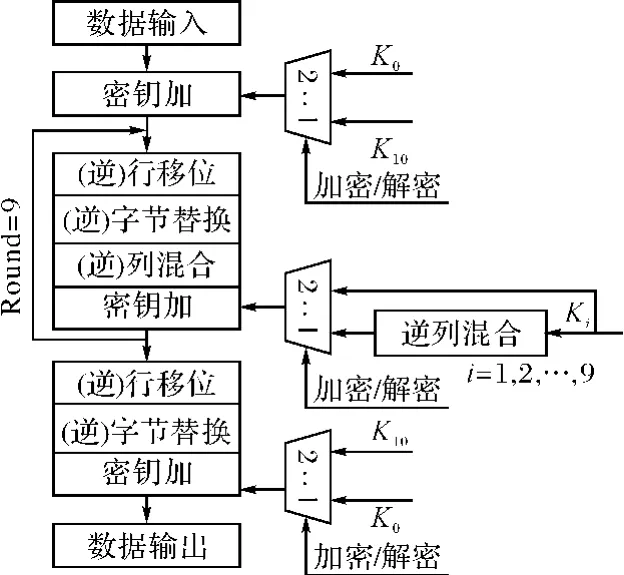
图1 AES加解密的复合结构图

在图1中，加解密完全共用一个迭代结构，只是在子密钥的调用方面有所不同，可以通过控制信号加密／解密进行选取控制。加解密结构可以复用，给轮变换中字节替换／逆字节替换、行移位／逆行移位、列混合／逆列混合操作进行电路结构复用优化提供了可能。

4 性能分析

本文采用QuartusII 7.1对算法的器件资源利用率进行了综合编译得到了如图2所示的编译结果。我们采用的器件是Altera公司的Cyclone II系列的EP2C35F672C8芯片，该芯片内嵌各种乘法器、RAM模块，具有丰富的引脚和存储资源，适用于信号的高速处理，在设计中只用来仿真算法的资源使用情况。

由图2可以看出，我们设计的AES算法硬件方案使用了芯片上262个I／O引脚（占55%），使用了33216个逻辑单元中的6915个（占21%），其中组合逻辑单元占用6272个，专用逻辑寄存器占用786个。由结果可以得出，通过复用技术对加解密结构的优化带来了资源上的优化，能够满足受限的RFID系统的面积要求。

图2 加解密系统的QuartusII综合编译结果图

5 结语

本文优化设计的AES算法利用电路模块的复用技术对算法进行优化处理，使算法加解密电路可以复用，实现在满足系统数据传输速率要求的前提下，最大限度地降低电路面积。应用于资源受限的RFID系统中，不但为其提供了十分可靠的安全保障，而且在有限的硬件环境下提高了其数据吞吐效率。

［1］中国射频识别（RFID）技术发展与应用报告蓝皮书［Z］.2009，10.

［2］范红梅.RFID技术研究［D］.杭州：浙江大学，2006：4-5.

［3］颜涛.RFID技术研究及其在仓储管理中的应用［D］.西安：西安电子科技大学，2006：6-10，13-7.

［4］董丽峰.RFID中间件技术在物联网中的应用及研究［J］.黑龙江科技信息，2010（2）：73-74.

［5］OHKUBO M，SUZUKI K，KINOSHITA S.Cryptographic approach to privacy-friendly tags［C］／／Proceedings of RFID Privacy Workshop，2003：11-17.

［6］FERGUSON N，SHROEPPEL R，WHITING D.A simple algebraic representation of Rijndael［C］／／Proceedings of Selected Areas in Cryptography.Las Vegas，USA：Springer-Verlag，2001：103-111.

［7］Ling Bing，Xia Kewei，Liang Wenli.Reconfigurable implementation of AES algorithm IP core based on pipeline structure［J］.Journal of Southeast University（English Edition），2010，26（1）：21-25.

［8］Batbold T，KyungOh L.An Advanced Mutual-Authentication Algorithm Using AES for RFID Systems［J］.International Journal of Computer Science and Network Security，2006，6（9B）：156-162.

［9］Ling Bing，Xia Kewei，Liang Wenli.Reconfigurable implementation of AES algorithm IP core based on pipeline structure［J］.Journal of Southeast University（English Edition），2010，26（1）：21-25.

［10］刘晗嘉.AES加密算法IP核的设计与验证［D］.上海：上海交通大学，2009.