基于数字仿真导引头抗干扰性能评估方法研究＊

李 敬 王 鑫 赵春晖

（1.哈尔滨工程大学 哈尔滨 150001）（2.中国航天科工集团公司8511研究所 南京 210007）

1 引言

随着科学技术的发展，作战目标干扰装备、技术体制、作战方式等日趋灵活多样，造成导弹攻击过程中导引头面临的电磁环境也复杂多变，严重制约了导弹武器系统发挥作用。因此，如何评价和研究在不同类型的干扰、不同程度的干扰条件下导引头的抗干扰能力，对于保证导弹武器系统发挥作用具有重要意义。

在目前的导弹武器系统效能评估方法中，几乎都建立了相应的评估模型，在不同的评估准则基础之上，按评估模型将导弹武器系统作战流程分解、量化，最后给出效能指标值［1］，例如 WSEIAC模型。张领军等人在文献［2］中，通过分析WSEIAC系统效能评估模型，提出了反舰导弹导引头抗干扰效能参数及其效能评估表达式。此类方法虽较客观地分析了效能评估问题，但却没有给出导弹效能指标，存在着实用性不强等缺点。

本文针对反舰导弹导引头系统，提出了一种将外场试验与数学仿真相结合的导引头抗干扰性能评估方法。建立反舰导弹自导段弹道仿真模型，将外场试验输出数据引入自导段弹道解算中，通过多次弹道仿真，最终给出反舰导弹导引头完成任务概率。解决了一些现有的评估方法评估结果不能直观反映导弹抗干扰能力的问题。

2 评估流程

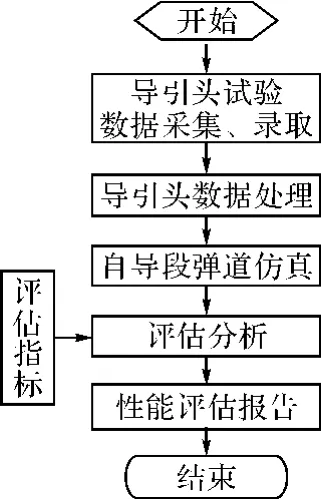
图1 评估流程图

反舰导弹导引头抗干扰性能评估，可以定义为针对导引头在电磁干扰环境下性能下降程度进行定量评估的一整套评估准则、指标集合和操作方法［3］。过去曾经有过不少研究，提出了多种评估准则：功率准则、信息准则、效率准则等。几种准则分别以雷达接收机干信比的变化、雷达接收机获取信息量的损失程度、武器系统完成作战任务的能力为评价依据，来衡量抗干扰性能好坏，然而军方所关心的是导弹武器系统命中目标的能力，即单发导弹命中概率，所以本文以效率准则为评估准则，以导引头捕捉概率、稳定跟踪概率以及导引头完成任务概率为评估指标，通过比较在有无干扰、不同等级干扰的条件下，上述指标的下降程度，来直观反映导引头的抗干扰能力，评估导引头的抗干扰性能。评估流程如图1所示。

导引头试验数据采集、录取工作在外场静态试验时进行，需采集、录取的数据包括靶场测控网提供的观测舰和目标舰的GPS位置信息以及导引头输出的距离、航向和俯仰等特征参数。

得到的导引头特征参数虽是通过大量数据表述的，但这些数据并不能与导弹飞行发生闭环控制［5］，因此不能直接用于弹道仿真。得到这些数据之后，首先应进行处理，生成导引头偏差数据。然后进行偏差数据空间转换，将静态试验导引头相对目标的偏差数据转化为导弹实际飞行时，相对于目标的偏差数据。最终生成导弹航控量数据并参与弹道仿真，模拟反舰导弹自导段飞行轨迹。评估分析中，依据导弹飞行数据，分析导引头完成任务能力，评估导引头的抗干扰性能。

3 导引头数据处理

反舰导弹导引头数据处理流程图如图2所示。

数据输入为靶场测控网提供的观测舰和目标舰的GPS位置信息以及导引头输出的距离、航向和俯仰等静态数据。这些数据在用于仿真之前需要进行坐标转换，将靶场测控网提供的观测舰、目标舰的经纬度及大地高（λ、φ、H）转换成地心坐标系（以地球质心为原点，Z轴与地球自转轴重合，X轴指向地面赤道平面与本初子午线的交点，Y轴垂直XOZ平面指向东［4］中的位置坐标，如图3所示。

图2 导引头数据处理

图3 坐标转换示意图

地理坐标变换到地心坐标的公式为

式中：N为椭球卯酉圈曲率半径；H为点沿法线至椭球的距离；e为椭球第一偏心率。

由地心坐标系平移成以试验点为原点的地面坐标系，转换公式为

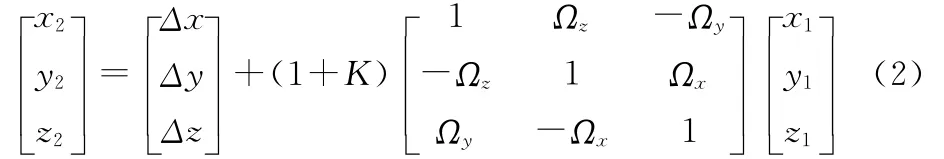
式中：x2，y2，z2—地面直角坐标系数据；Δx，Δy，Δz为平移转换参数，即地心坐标在地面坐标系中的坐标；Ωx，Ωy，Ωz为两坐标轴之间的旋转角；x1，y1，z1为地心坐标系数据；K为尺度因子。

为了弹道设计方便，定义平台坐标系，该坐标系以观测舰的初始位置作为坐标系的原点，以观测舰和目标舰的初始位置水平投影的连线作为x轴，x轴和z轴所在平面为水平面，y轴垂直于水平面，x、y和z轴三者满足右手坐标系，反舰导弹的初始位置在y轴上。地面坐标系平移到平台坐标系转换公式同式（2）。

坐标转换后的导引头数据需进行截取和滤波。截取是按时戳（时／分／秒）对观测舰数据、目标舰数据、导引头偏差数据（导引头输出数据处理所得）进行截取，分选仿真时间段内所用的试验数据。

试验数据滤波是对导引头航向角偏差、俯仰角偏差和距离偏差去奇异值处理。试验数据在录取的过程中，由于外界或人为原因，会出现一些奇异值，在使用前需进行去异处理，平缓试验数据，一般采用低通滤波。

4 自导段弹道仿真

反舰导弹的弹道仿真主要模拟反舰导弹的实际飞行过程。输入数据为经数据处理后的观测舰、目标舰的GPS位置信息、观测舰相对目标的俯仰角和偏航角偏差等静态数据。根据观测舰、导弹、目标舰三者之间的三维关系，将该试验静态数据转化为导弹实际飞行时，相对于目标舰的俯仰角和偏航角偏差数据。输出为导弹俯仰角、方位角和脱靶量等信息。

在分析过程中发现，若想将处理后的偏差数据引入到反舰导弹和目标舰的相对运动关系中，关键在于将观测舰相对于目标舰航向偏差和俯仰偏差转换为导弹实际飞行时，反舰导弹相对于目标舰的航向偏差和俯仰偏差［5］。偏差转换示意图如图4所示。

图4 偏差转换示意图

本文采用虚拟目标比例导引方式设计仿真弹道，导弹、固定目标与虚拟目标三者之间的相对位置关系如图5所示。

图5 虚拟目标比例导引模型示意图

图中各符号的含义是：（xm，ym）为导弹的瞬时位置，（xT，yT）为虚拟目标的瞬时位置，Ψm、vm为导弹的方位角和速度，ΨT、vT为虚拟目标的方位角和速度。am、aT分别为导弹与虚拟目标的加速度，σ为视线角。由图5可得到如下关系式：

在比例导引法中，导弹的速度矢量vm的转动角速度˙Ψm与视线的转动角速度˙σ成正比，所以导引方程为

虚拟目标比例导引参数选取k由式（10）确定，其中虚拟目标运动的速度为导弹速度的c倍，导弹初始的速度方向为ψm0，末端导弹的速度方向为Ψmf，视线角初始值为σ0，末端值为σf。

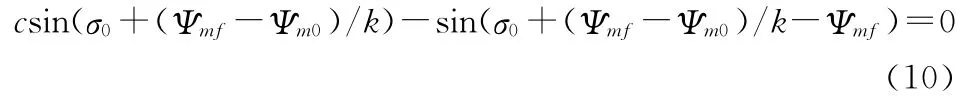
因此，可以得到比例导引控制信号为

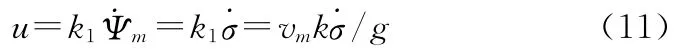
我们假设导弹在运动过程中速度近似为匀速，而控制力与速度垂直，从而只改变导弹速度的方向，则有：

以上为完整的比例导引运动关系模型，其中a′m为速度矢量的vm的横向加速度。按时间顺序获得处理后导弹弹道参数（xi，yi）和导引头输出数据，得到导弹控制量u，然后以该控制量为参量，处理得到下一时刻的导弹弹道参数（xi＋t，yi＋t）。以此类推，得到导弹自导段仿真弹道。

现假设一典型飞行过程：导弹以15°的初始偏航角，先在低空巡航飞行（飞行高度约为15m左右），在接近目标13～18km时，跃升至100m左右，然后进行俯冲攻击。在飞行过程中，不断纠正初始偏航角，最终击中目标。

目标的运动方式有两种，一是采用实际目标的位置数据，在每一步，读取目标数据。另外一种则是自行设定目标的运动方式，设定参数包含目标的航向角和目标速度等，目标沿设定偏航角匀速运动。

图6 俯视图

目标舰模型为长方体，目标长度、目标高度、目标宽度表示目标模型的尺寸，其尺寸可调。按仿真试验需求，读取实际目标位置数据，按比例导引方式对反舰导弹自导段分别进行侧向，纵向以及三维弹道仿真，仿真结果如图6、图7、图8所示。

图7 侧视图

图8 三维图

5 评估分析

能够直接反映反舰导弹武器系统抗干扰能力的指标是其单发导弹命中概率。对于反舰导弹导引头分系统，即导引头完成任务概率，用此概率反映导引头在不同阶段达到或完成一组特定任务要求的程度。反舰导弹导引头主要任务是保证导弹在自导阶段能够顺利捕捉并稳定跟踪目标，因此，可将反舰导弹导引头抗干扰性能分析与评估的内容分解为对导引头捕捉目标能力、稳定跟踪目标能力的分析与评估，评估指标为导引头捕捉目标概率、稳定跟踪概率以及导引头完成任务概率。通过比较有无干扰条件下的捕捉目标概率、稳定跟踪概率和导引头完成任务概率变化来评估导引头的抗干扰能力。

1）捕捉概率变化量ΔPbz的综合评估

通过在无干扰和有干扰条件下的试验［6～7］分别统计得到导引头捕捉概率Pbz、P′bz，就可以得到捕捉概率变化量ΔPbz＝Pbz－P′bz。捕捉概率变化量ΔPbz越大，说明导引头在有干扰条件下捕捉目标概率下降越多，则导引头抗干扰能力越差；反之，则导引头抗干扰能力越好。

2）稳定跟踪概率变化量ΔPgz的综合评估

通过在无干扰和有干扰条件下的试验分别统计得到导引头稳定跟踪概率Pgz、P′gz［8］，就可以得到 稳定跟踪概 率变化量ΔPgz＝Pgz－P′gz。稳定跟踪概率变化量ΔPgz越大，说明导引头在有干扰条件下稳定跟踪概率下降越多，则导引头抗干扰能力越差；反之，则导引头抗干扰能力越好。

3）导引头完成任务概率的综合评估

结合仿真过程，计算目标与导弹之间的距离，并与目标模型长度、宽度进行比较。当该距离等于或小于目标模型长度、宽度时为命中目标；当大于目标模型长度、宽度时，可视为脱靶［9～11］。最后统计多次仿真结果，得出导引头完成任务概率。通过比较导引头完成任务概率下降程度，可以反映导引头抗干扰能力的好坏，给出反舰导弹导引头抗干扰性能的评估结果。

6 结语

本文针对反舰导弹导引头抗干扰性能评估问题，利用导引头外场试验数据进行弹道仿真，将导引头完成任务概率作为评估指标，形成一套较完善的外场试验与数学仿真相结合的评估方法。本方法可进行多次仿真，重复性好，消耗低，并且采用导引头外场试验输出数据，具有较高的置信度，能够定量给出反映反舰导弹导引头抗干扰能力的指标值，满足评估要求。

［1］陆伟宁等.弹道导弹攻防对抗技术［M］.北京：中国宇航出版社，2007，4：294-297.

［2］张领军，孙希东.反舰导弹导引头抗干扰效能评估［J］.航天电子对抗，2005，21（6）：1-4.

［3］王国玉，汪连栋.雷达电子战系统数学仿真与评估［M］.北京：国防工业出版社，2004（6）：56-93.

［4］GJB 530A-2006反舰导弹末制导雷达海上试验规程［S］.中华人民共和国国家军用标准，2006.

［5］梁斌，王鑫，张领军.反舰导弹末制导雷达抗干扰试验的数据处理［J］.航天电子对抗，2010，26（1）：18-20.

［6］王国玉，王连栋.雷达对抗试验替代等效推算原理与方法［M］.国防工业出版社，2002：10-25.

［7］GJB 6091-2007.弹道导弹导引雷达抗干扰内场仿真试验方法［S］.中华人民共和国国家军用标准，2007.

［8］盛骤.概率论与数理统计［M］.高等教育出版社，2001，1：6-29.

［9］章耐芳.反舰导弹末制导雷达抗干扰设计方法［J］.航天电子对抗，1994（4）：19-22.

［10］戴逸俊.反舰导弹末制导雷达面临的电子战环境与对策［J］.航天电子对抗，1996（1）：15-20.

［11］王永.雷达／红外成像复合制导面临的干扰及对抗［J］.舰船电子工程，2010（4）：14-17.