基于网络分析法的舰舰导弹性能评估方法研究＊

任 伟 熊 鹰 张树龙

（海军工程大学船舶与动力学院 武汉 430033）

1 引言

舰载武器系统方案的评估与优选是舰船作战系统研制、论证过程中的重要环节，决定了武器系统的作战效能。舰舰导弹是攻击敌方舰船的主要武器，正确分析、评估舰舰导弹的作战性能，建立其战术技术指标体系，研究其评估模型，可以为舰船作战系统装备选型提供依据。传统的性能评估方法包括层次分析法（AHP）、效用函数（AUT）、系统分析法（SEA）、Petri网法等［1～4］。其中层次分析法应用的最为广泛，国内外学者多使用AHP计算舰载武器的性能指标值（VOPs）［5～7］。

然而层次分析法的核心是将系统划分层次且只考虑上层元素对下层元素的支配作用，同一层次中的元素要求彼此独立，这种层次递阶结构虽然结构清晰，使用方便，但也限制了它在复杂决策问题中的应用。舰舰导弹是一种复杂的武器系统，其性能指标之间存在着相互影响、相互依赖的关系，这是一种具有反馈的网络结构。网络分析法（ANP）正是一种具有反馈网络结构的定量分析方法，由美国匹兹堡大学教授Thomas L.Saaty在1996年提出。这种方法能够处理指标元素间的相关关系，适应非独立递阶层次结构［8～9］。本文探讨了应用ANP对舰舰导弹方案选择问题进行建模。

2 网络分析法的基本原理

2.1 ANP的结构

网络分析法由两部分组成，第一部分为控制层，包括准则网络及准则子网络，控制着系统的交互作用。第二部分是网络层，是表示元素之间影响的网络结构。相类似的元素构成元素簇，元素簇中不同元素间两两相互比较构成影响关系的网络。同簇内元素相互比较为内部相关关系，不同簇之间元素相互比较为外部相关关系。如图1所示。

从C1连接到C2的箭头代表着在某种准则下，C1中的元素与C2中的元素具有外部相关关系；C1和C3的环形箭头代表着簇内元素具有内部相关关系。ANP需要对存在相关关系的元素在某种准则下进行成对比较，确定优势度并由此获得判断矩阵。通常采用的成对比较方法为问卷调查法、矩阵法、图形法等。

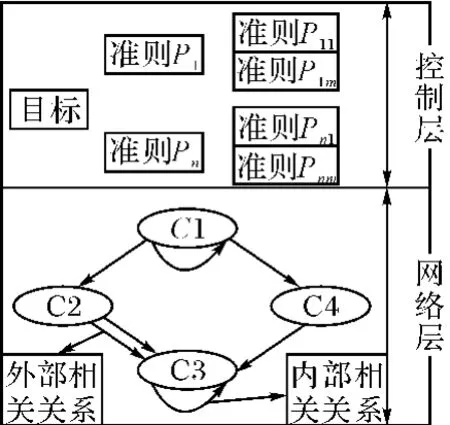
图1 ANP的一般结构

2.2 超矩阵

2.2.1 判断超矩阵

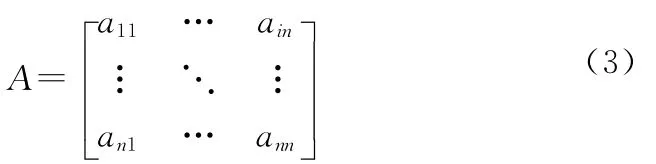
超矩阵代表了在控制层的某种准则下矩阵左侧元素相对于矩阵顶部元素的影响优势度，由成对比较得到的优势度矩阵构成超矩阵的子块。式（1）代表了超矩阵的一般模型。假设控制层的准则为P1，…，Pn，网络层的元素簇为C1，…，Cn，其中Ci中的元素为ei1，…，eini，i＝1，…，N。以控制层元素Ps为准则，以Cj中的元素ejk为父节点，元素组Ci中元素按其对ejk的影响力大小进行优势度比较即可得到判断超矩阵。

对每个比较矩阵求特征值和对应的排序特征向量，记为Wij，如式（2）所示：

Wij的列向量就是Ci中元素ei1，…，eini相对Cj中元素ej1，…，ejnj的影响程度排序向量。如果Ci中的元素对Cj中元素没有影响，则Wij＝0。超矩阵的数目等于控制层的准则数目。超矩阵都是非负矩阵，其子块Wij均是列归一化的，但是W却不是列归一化。为此以PS为准则对各元素簇的重要程度进行成对比较得到优势度，由此得到簇权重矩阵A。

2.2.2 加权超矩阵

2.2.3 极限超矩阵

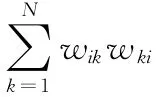
3 性能评估模型

3.1 评估指标体系的建立

舰舰导弹同舰艇上的导弹射击控制系统、探测跟踪设备、水平稳定设备以及发射设备共同构成了舰舰导弹系统。系统的主要战术技术性能包括系统作用范围、作战火力、反应时间、系统精度、系统可靠性以及系统使用环境条件六个方面。系统的作用范围主要由最大作用距离、最小作用距离、作用扇面以及导弹射角构成，最大作用范围由探测雷达决定，最小作用距离由导弹的最小射程决定；作战火力考虑了导弹的总数量、同舷目标最大导弹发射数量、单发命中概率以及射击通道四个方面；系统反应时间有两种，从接收到目标指示至导弹发射的系统反应时间以及从雷达发现目标至导弹发射的时间；系统精度包括导弹自控飞行时间误差、前置航向误差、俯仰角误差以及滚动角误差；系统可靠性考虑平均无故障时间MTBF以及平均修复时间MTTR；系统环境要求考虑了温度、湿度、海情以及特定电磁环境下能够安全工作的能力。基于以上分析，建立了如图2所示的性能评估指标体系。

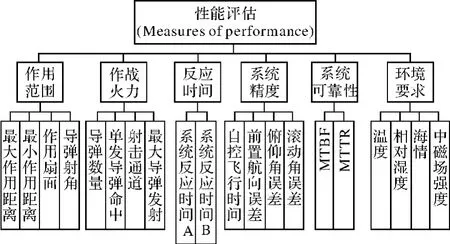
图2 性能评估指标体系

图3 AHP评估模型

3.2 评估模型的建立

依据ANP建模要求，控制层中选取舰舰导弹系统战术技术性能为评估准则，网络层中包含方案集合、系统作用范围、作战火力、反应时间、系统精度、系统可靠性以及系统使用环境条件七个指标簇，每个指标簇中的指标同性能评估指标体系，使用SUPERDECISION软件建立如图3所示的ANP评估模型。单相箭头代表一个簇中的指标受另外一个簇中的指标影响；环形箭头代表同簇中的指标之间相互影响；双向箭头代表两个簇中的指标相互影响。

3.3 判断矩阵和一致性检验

采用基于问卷表的九级标度法确定元素之间的比较优势度。图4为以方案簇中方案A为父节点，对作用范围指标簇中元素进行成对九级标度法比较。判断矩阵建立后，需要进行一致性检验，即保证所有的判断矩阵CR指标小于0.1，本例中CR＝0.0163＜0.1，符合要求。

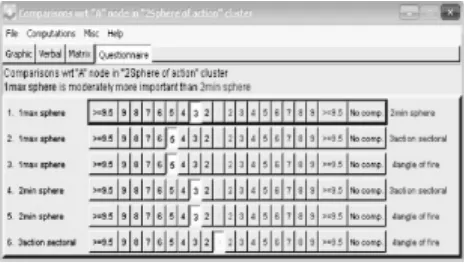
图4 作用范围比较优势度赋值

图5 一致性检验

4 评估结果

使用SUPERDECISION计算得到舰舰导弹战术技术性能评估模型的簇权重矩阵如图6所示。

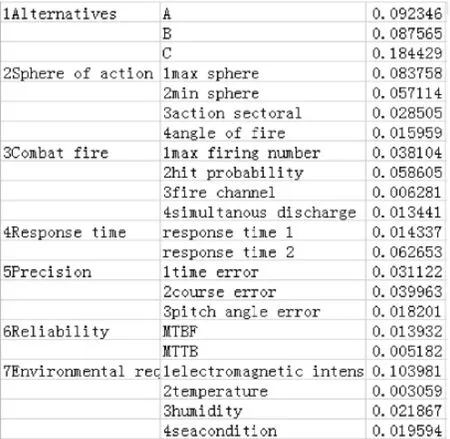
图6 簇权重矩阵

对超矩阵进行加权并升幂取极限得到的极限超矩阵如图7所示。

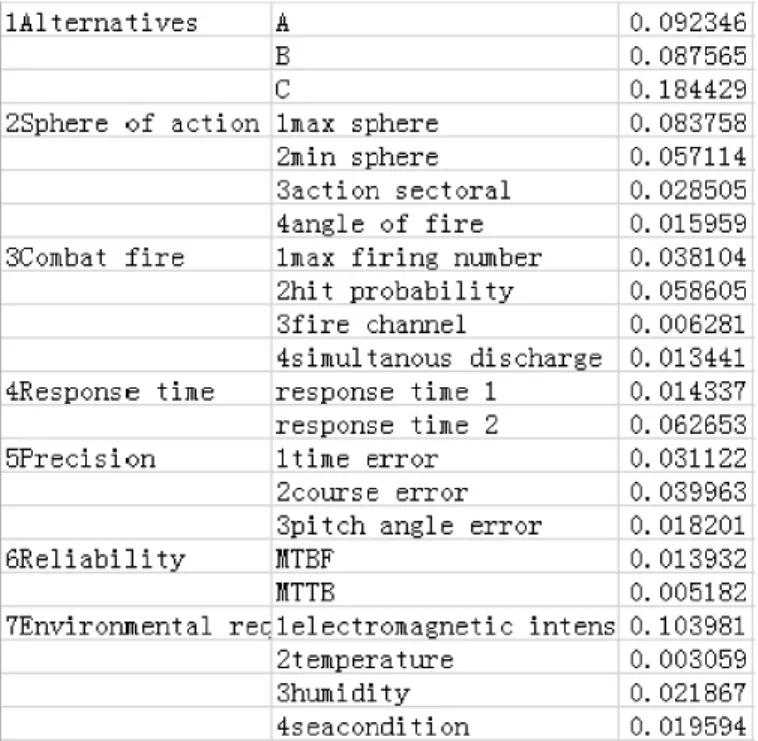
图7 极限超矩阵

最终得到的综合优势度如表1所示，其中正规化是将初始值进行列随机化使之和为1，理想化为各元素除以列中元素最大值。理想化的方案综合优势度可以作为舰载武器的性能指标值（VOPs），用来计算舰艇作战系统的综合效能值OMOE。

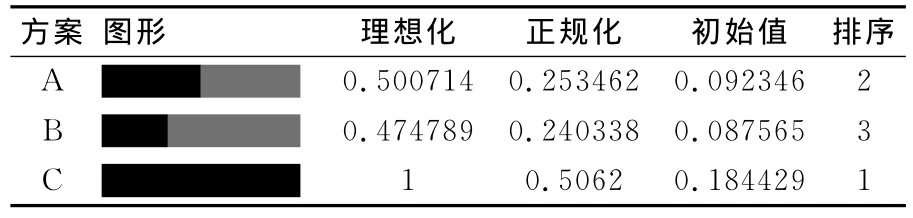
表1 各方案的综合优势度

在实际的舰舰导弹方案中，由于方案C具有最大的雷达视距以及最强的作战火力，其作战性能要优于方案A和方案B，计算结果与实际相符。

5 结语

ANP是一种具有严格数学证明的决策方法，其核心算法是有关超矩阵的运算。超矩阵的计算比较复杂，但是我们可以借鉴相关软件进行求解。利用ANP对舰舰导弹系统战术技术性能评估可以充分考虑影响系统性能的各个方面，尤其是评估指标之间的相关性。ANP比层次分析法更加客观的计算了各个方案的性能指标值，为舰艇作战系统方案选型提供了有力支持。文中只考虑了战术技术性能单一准则，如何在性能、风险、费用等多准则下的建模是以后研究的重点。

［1］徐瑞恩.武器装备效能模型和方法概论［J］.装备指挥技术学院学报，2002，13 （1）：1-5.

［2］Thiel，S.Petri Net Based Verification of Causal Dependencies in Electronic Control Unit Test Cases［J］.Computer Software and Applications Journal，2011，35（1）：113-117.

［3］Rajarshi Das.Utility-function-driven energy-efficient cooling in data centers［J］.Autonomic Computing Journal，2008，26（3）：61-70.

［4］Nachiappan Subramanian.AReview of Applications of Analytic Hierarchy Process in Operations Management［J］.International Journal of Production Economics，2012，138（2）：215-241.

［5］BROWN A J.Multiple objective genetic optimization in naval ship design［J］.Naval Engineers Journal，2003，115（4）：49-61.

［6］STEPANCHICK J.Revisiting DDGX／DDG-51concept exploration［J］.Naval Engineers Journal，2007，119（3）：67-88

［7］Demko D.Tools for multi-objective and multidisciplinary optimization in naval ship design thesis［D］.USA：Virginia Polytechnic and State University，2005.

［8］Saaty T L.The Analytic Network Process［M］.Pittsburgh：RWS Publications，1996.

［9］Saaty T L.Theory and Applications of the Analytic Network Process［M］.Pittsburgh：RWS Publications，2006.

［10］王莲芬.网络分析法（ANP）理论和算法［J］.系统工程理论和实践，2001，21（3）：44-50.