一种基于位置误差检测门限的机动目标跟踪算法＊

汤传贵 张 珂 晁爱民 张国栋

（1.海军驻青岛造船厂军事代表室 青岛 266001）（2.海军工程大学 武汉 430033）

1 引言

在现代跟踪系统中，对匀速目标的跟踪是很容易实现的，但对于机动目标的跟踪就比较困难，原因在于很难建立精确的机动目标模型。研究人员做了大量的工作，提出了许多模型，其中周宏仁等人提出的机动目标“当前”统计模型［1］是目前较好的一种。由于这些模型自身的局限，单独采用一个模型进行滤波精度不高。为此，Bar—Shalom和Blom等人在广义伪贝叶斯算法的基础上，提出了一种具有马尔可夫切换系数的交互式多模型（IMM）滤波算法［2～3］，其中多个模型并行工作。模型间以概率矩阵进行转移，目标状态估计是多个滤波器交互作用的结果，该算法不需要机动检测，达到了全面自适应的目的。

但是在实际的MM算法运行过程中，总模型集里仅仅只有一小部分模型对整体状态的估计有较大作用。因此，在任何时刻都使用固定的模型集是不合适的，以上算法中的限制可以通过时变模型集的方法解决，这种方法被称为变结构多模型（VSMM）算法，由 Li X R［4］和 Kirubarajan［5］等人所提出。VSMM算法可以看作是普通的定结构多模型算法（FSMM）加上一个利用当前时刻状态调整使用模型的控制模块。在VSMM算法的设计中，不仅需要像FSMM算法一样考虑所有可能模型集合，还需要考虑在某一时刻如何选择使用有效的模型集合，从而达到降低算法运算负荷的目的。

本文通过对位置误差的检测实现模型集合自适应，属有向图切换法。基于位置误差检测的VSMM算法与IMM算法的仿真实验比较结果说明了该算法的有效性。

2 基于RAMS的VSMM算法简介

理想的VSMM算法应该分成两层结构，上一层为多模型集合序列，下一层为模型集合内的多模型序列，整体状态估计由下式给出［6］：

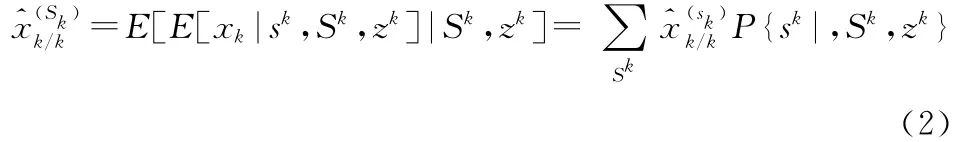
VSMM算法的两级融合结构如图1所示。

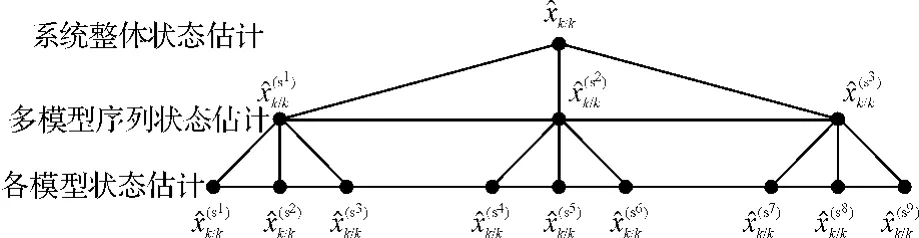
图1 VSMM算法两级融合结构示意图

3 基于位置误差检测的VSMM算法

本文采用极坐标系下的量测模型和直角坐标系下的状态模型进行目标跟踪理论的研究。以我舰观测雷达为原点建立空间直角坐标系，则目标在直角坐标系内的运动情况如图2所示。

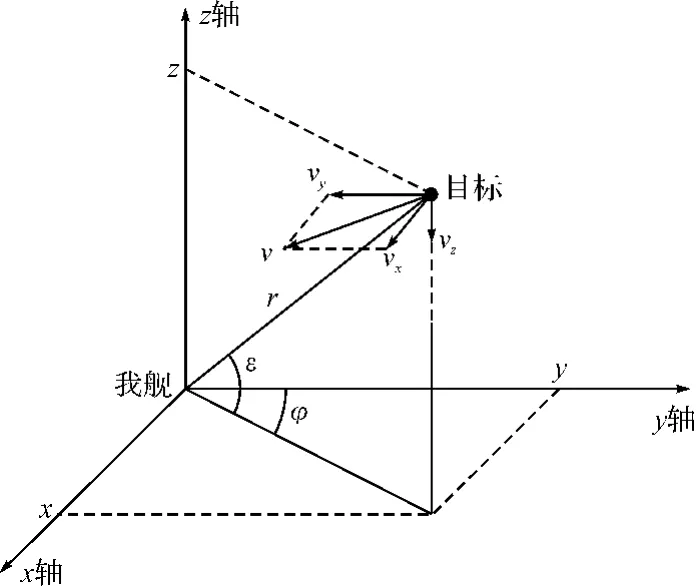
图2 火控滤波直角坐标系及目标运动情况

参照图2，假设目标在水平面内做匀速直线运动，r、φ、ε是观测雷达输出的斜距、方位角、俯仰角信息，设斜距、方位角、俯仰角的随机观测误差均方差分别为σr、σφ、σε，同时忽略系统误差。

由此可见，二甲双胍能有效地延缓AS的进展，对T2DM患者心血管系统具有一定的保护作用。但由于受伦理道德原则、《药物临床试验质量管理规范》（GCP）和相关法律法规的约束，目前该方面临床研究还相对较少，其结论仍有待进一步验证。

假设初始速度和位置为零，极坐标系与直角坐标系之间的关系如下：

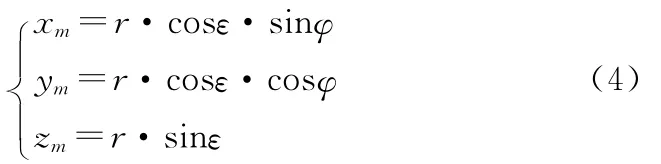
3.1 模型集合设计

由于目标作转弯机动时除了位置和速度信息的变化外，还存在着高低角和方位角信息的变化，并且测量信息在三维直角坐标系下是相互耦合的，因此传统VSMM算法对三维空间中目标的转弯机动跟踪效果较差，而对目标的匀速、匀加速机动跟踪效果较好。基于以上原因，本文模型集的设定将主要针对目标的转弯机动。设定以下6个模型集，模型集中包含各子模型：

模型集1：｛匀速直线运动目标（CV）跟踪模型；匀加速直线运动目标（CA）跟踪模型｝

模型集2～模型集6为不同高低角变化率的匀速圆周运动目标（CT）跟踪模型组合，每一个模型集里面包含四个不同高低角变化率和方位角变化率的CT跟踪模型。

上述模型集中，模型集1针对目标的直线运动，模型集2～6针对目标的曲线运动，各模型集中的子模型均为典型单目标跟踪模型［8～9］。

3.2 机动检测准则设计

采用滑窗式［7］检测法，记当前时刻位置滤波误差为D，检测门限为m。当D＞m时，判定目标发生机动；当D＜m时，判定目标机动消除。

3.3 最佳模型集合选择准则设计

若模型集1的IMM滤波结果符合机动检测准则，则确定目标做直线运动，该集合为最佳模型集合；若模型集2～6中某一模型集的IMM滤波结果符合机动检测准则，则确定目标做曲线运动，该集合为最佳模型集合。

3.4 VSMM算法流程

以观测系统输入的第一次观测值为滤波器的初值，滤波器从k＝1开始工作。

2）算法描述

Step1：对VSMM进行初始化，输入初值X1，P1；

Step2：对各模型集进行IMM滤波；

Step3：判断出各模型集中新息残差最小的模型集a，输出模型集a的滤波结果；

Step4：更新量测值；

Step5：对模型集a进行IMM滤波，若滤波结果未检测到目标机动，则输出模型集a的滤波结果；若滤波结果检测到目标机动，则激活其它模型集，并利用a在k－1时刻的结果对各模型集进行重新初始化；

Step6：是否停止解算？是，结束；否则，转Step3。

流程图如图3所示。

图3 VSMM滤波算法流程图

4 仿真实现

为了验证本文所提算法的有效性，对本文算法与传统IMM算法进行蒙特卡洛仿真实现，并对两种算法的跟踪性能进行比较分析。

4.1 仿真初始设定

设目标在三维空间内进行机动，前2s做速度为850m／s的匀速直线运动，2～6s做加速度100m／s的匀加速运动，6～10s做方位角速度0.2rad／s、高低角速度0.1rad／s的匀速转弯运动：初始斜距11325m；雷达采样率50Hz；采样持续时间10s；观测距离随机误差5m；观测距变率随机误差2m／s；观测方位角、高低角随机误差0.9mrad；观测方位角、高低角变化率随机误差0.5mrad／s。

4.2 仿真结果

图5～图10显示，对x、y轴位置信息来说，在目标尚未发生机动的0～2s，两种滤波算法的效果相差不大，这是由于两种算法采用同样跟踪子模型进行滤波的原因；但在目标机动发生后，VSMM算法的滤波效果要明显好于IMM算法；对x、y轴速度信息来说，不论目标是否作机动，VSMM的滤波效果始终好于IMM；两种算法对z轴位置信息和速度信息的滤波效果相差不大。这说明采用本文的机动检测方法后，滤波算法对三维空间中作机动的目标跟踪能力有了较明显提高，但对于不作机动的目标而言，跟踪效果改善并不明显。

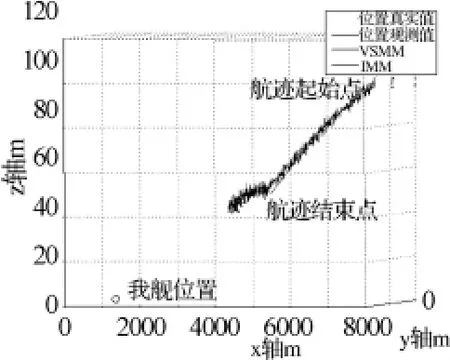
图4 目标运动轨迹及两种滤波模拟

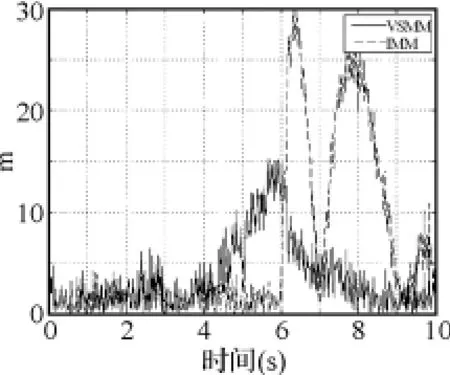
图5 x方向的位置滤波误差比较图

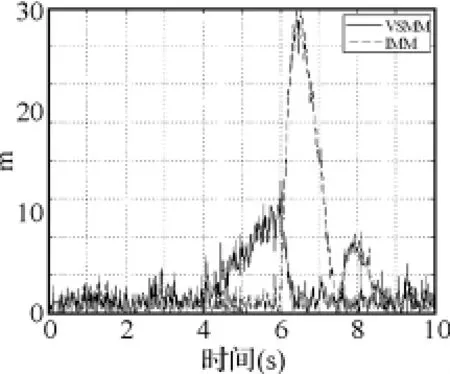
图6 Y方向的位置滤波误差比较图

图7 Z方向的位置滤波误差比较图

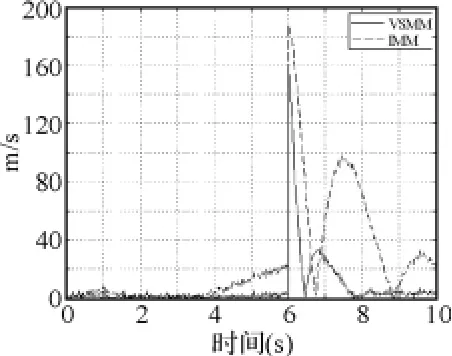
图8 X方向的速度滤波误差比较图

5 结语

本文在分析典型多模型算法（IMM）不足的基础上，通过改进现有变结构交互多模型算法（VSMM），将检测门限设置为目标跟踪位置误差门限，根据对目标位置信息的误差检测来判定目标是否作机动。仿真实验证明，该方法可有效提高多模型算法对三维空间机动目标的滤波效果，具有一定理论价值。

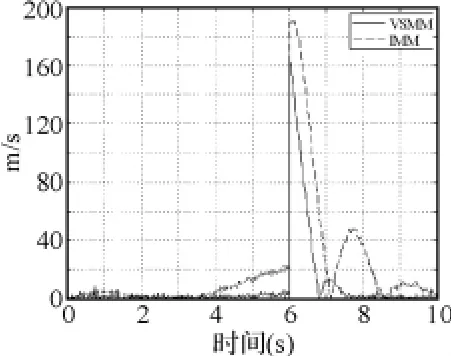
图9 Y方向的速度滤波误差比较图

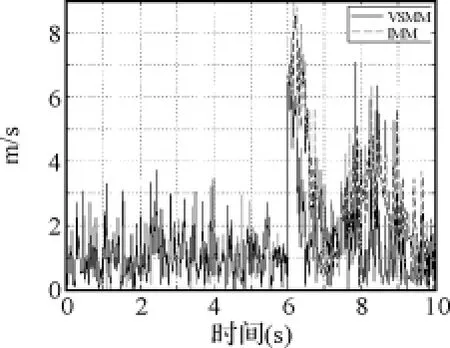
图10 Z方向的速度滤波误差比较图

［1］周宏仁，敬忠良.机动目标跟踪［M］.北京：国防工业出版社，1991：19-21，25，31-32.

［2］Blom H A，Bar-Shalom Y.The Interacting Multiple Model Algorithm for Systems with Markovian Switching Coefficients［J］.IEEE Trans.On Automatic Control，1988，33（8）：780-783.

［3］Mazor E，Averbuch A，Bar-Shalom Y，et al.Interacting Multiple Model Methods in Target Tracking：A Survey［J］.IEEE Trans.On Aerospace and Electronic Systems，1998，34（1）：103-123.

［4］LI X R，Bar-Shalom Y.Multiple Model Estimation with Variable Structure［J］.IEEE Transactions on Automatic Control，1996，24（1）：478-493.

［5］Kirubarajan T，Bar-Shalom Y，Pattipatik P，et al.Ground Target Tracking with Variable Structure IMM Estimator［J］.IEEE Transactions on Aerospace and Electronic Systems，2000，36（1）：26-44.

［6］A.T.Alouani，P.Xia，T.R..Rice，et al.Two-stage Kalman eastimator for tracking maneuvering targets［J］.Conf.Proc.1991IEEE International Conference on systems，Man，and Cybernetics.Decision Aiding for Complex Systems，1991（2）：761-766.

［7］范红旗，王胜，付强.目标机动检测算法综述［J］.系统工程与电子技术，2009（5）：1064-1070.

［8］何友.雷达数据处理及应用［M］.北京：电子工业出版社，2005：132-137.

［9］石章松，周丰，孙世岩.目标跟踪与数据融合理论及其应用［M］.武汉：海军工程大学，2007：145-217.